the position vector of the centre of mass lt
→
r cm of an asymmetric uniform bar of negligible area of cross - section as shown in figure is :
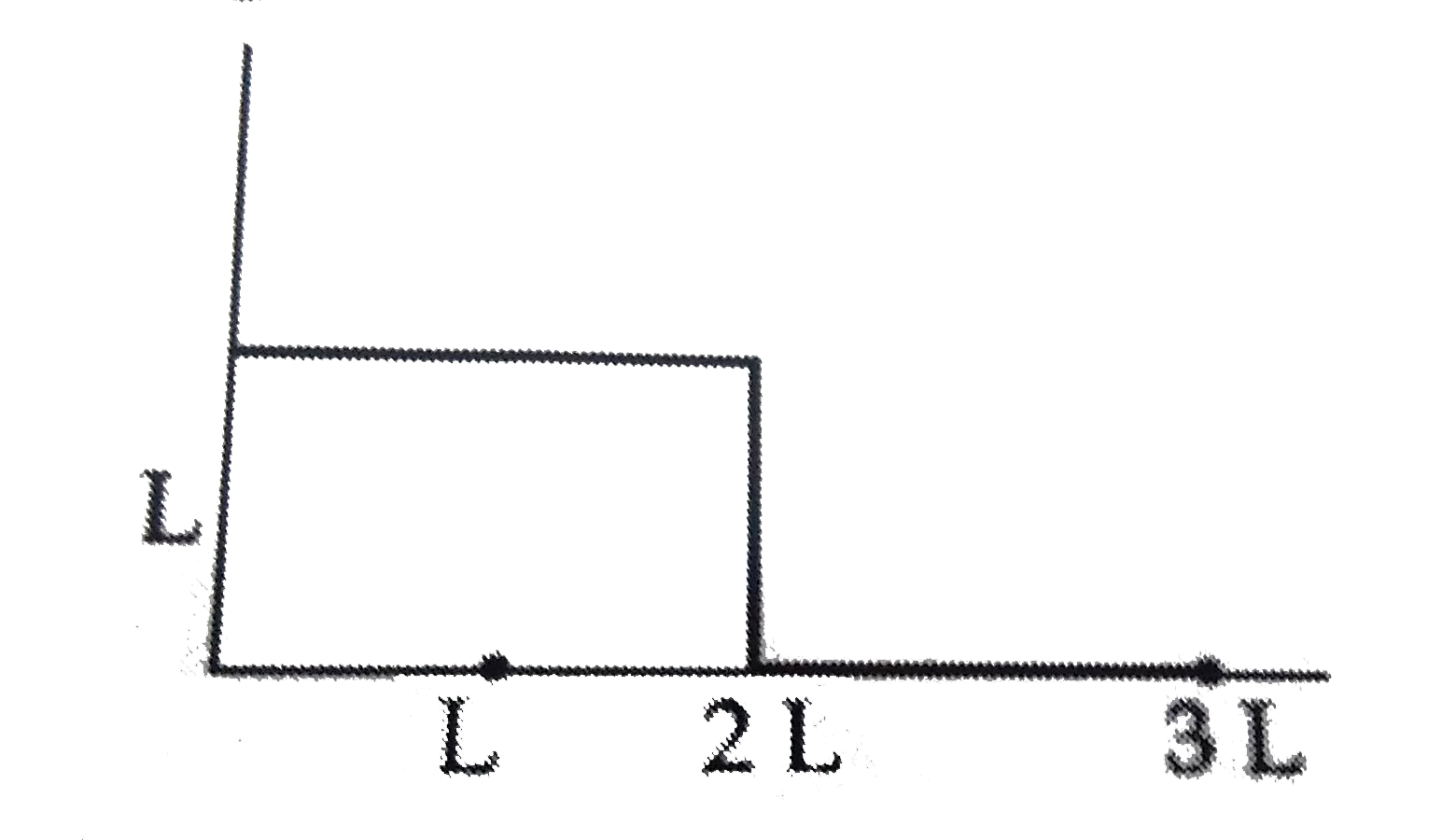
→Fcm=38Lˆx+118Lˆy
→Fcm=118Lˆx+38Lˆy
→Fcm=138Lˆx+58Lˆy
→Fcm=58Lˆx+138Lˆy
The correct Answer is:C
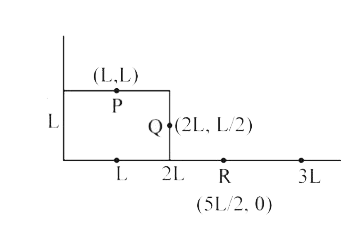
m1=2m, m2=m, m3=m
We can assume the com of the three rods located at P, Q,
Xcom=m1x1+m2x2+m3x3m1+m2+m3
=m4m(2L+2L+5L2)=13L8
Ycom=m1Y1+m2Y2+m3Y3m1+m2+m3, Ycom=2m×L+m×L/2+mx×om1+m2+m3=m4m(2L+L/2)=5L8 .
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE)80videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - PARAGRAPH QUESTIONS5videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - LEVEL - 2 PARAGRAPH QUESTIONS2videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)89videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )111videos
GASEOUS STATE & THERMODYNAMICS
Similar Questions
Knowledge Check
- Question 1 - Select One
The position of the centre of mass of a cube of uniform mass density will be at
Athe centre of one faceBthe centre of the interaction of diagonals of one face.Cthe geometric centre of the cubeDthe edge of a cube
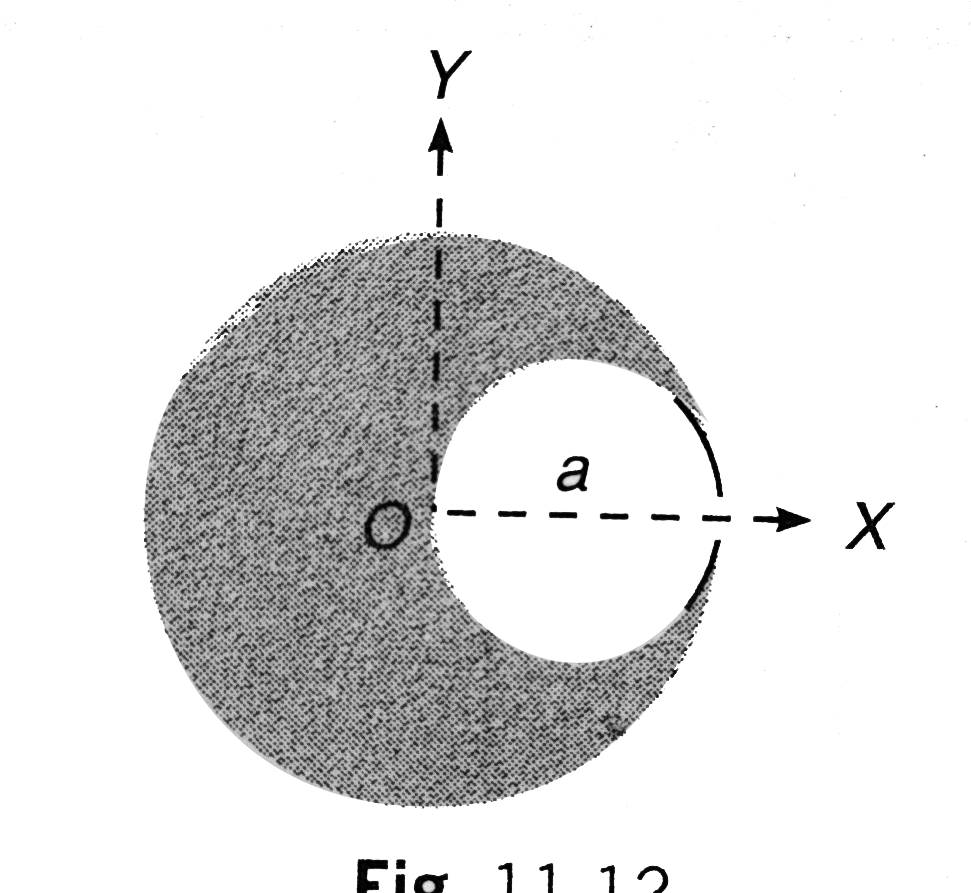
Find the position of centre of mass of the uniform lamina shown in figure.
 View Solution
View SolutionMagnetic field strength at the centre of regular pentagon made of a conducting wire of uniform cross section area as shown in figure is:
 View Solution
View SolutionThe distance of center of mass from the center of a uniform disc of radius R. if a circular plate is removed from the disc as shown in figure will be (C is centre of complete disc)
View SolutionDetermine the centre of mass of a uniform hemisphere of radius R.
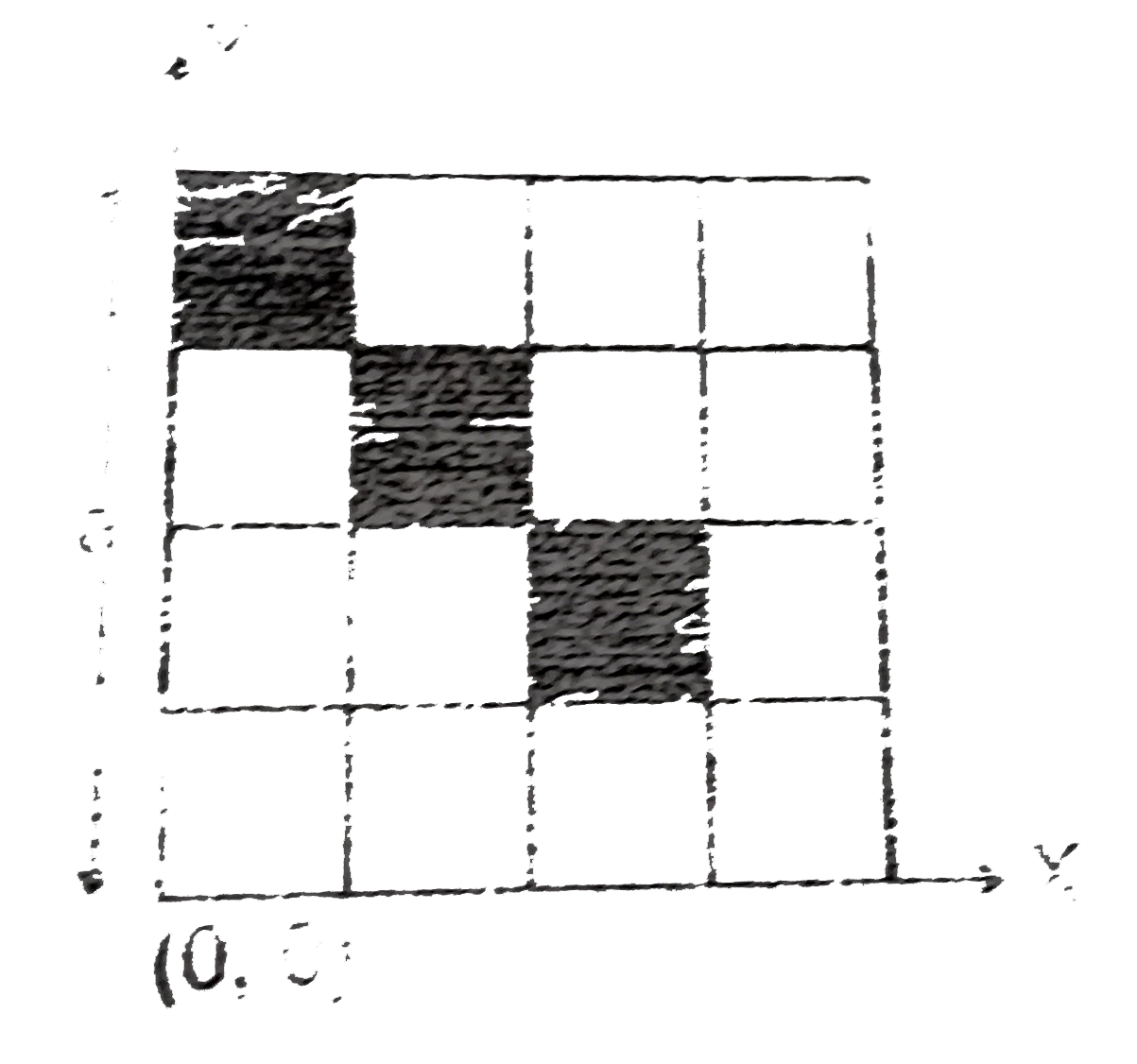
View SolutionFrom a uniform square plate the shaped portions are removed as shown in figure. The coordinates of centre of mass of the remaining plate are x,y Axes and origon are shown in figure.
 View Solution
View SolutionResistance of a conductor of length l and area of cross-section A is R. If its length is doubled and area of cross-section is halved, then find its new resistance.
View SolutionResistance of a conductor of length l and area of cross-section A is R. If its length is doubled and area of cross-section is halved, then find its new resistance.
View Solution



 .
.