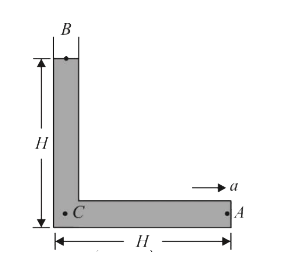
For the L-shaped vessel shown in the figure, determine the value of acceleration a so that pressure at point A becomes equal to p0/2? (p0 is the atmospheric pressure)

g
g2+P02ρH
P02ρH+g
3P02ρH+g
The correct Answer is:C
⇒PC−PA=ρaH
⇒P0+ρgH−P02=ρaH
⇒a=(P02ρH+g)
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - LEVEL -250videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE MAIN (LEVEL - 1 )31videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - LEVEL-0 ( Short Answer Type - II )15videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE53videos
LAWS OF MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)78videos
MAGNETIC EFFECTS OF CURRENT
Similar Questions
Knowledge Check
- Question 1 - Select One
The density of water at the surface of ocean is ρ . If the bulk modulus of water is B, then the density of ocean water at depth, when the pressure at a depth is αp0 and p0 is the atmospheric pressure is
AρKk−nP0BρKK+nP0CρKK−(n−1)P0DρK(K+(n−1)P0)
Figure shows an L-shaped tube tilled with a liquid to a height H. What should be the horizontal acceleration a of the tube so that the pressure at the point A becomes atmospheric.
 View Solution
View SolutionThe air tight and smooth piston of a cylindrical vessel are connected with a string as shown. Initially pressure and temperature of the gas are P0 and T0. The atmospheric pressure is also P0. At a later time, tension in the string is 38P0A where A is the cross-sectional are of the cylinder. at this time, the temperature of the gas has become.
 View Solution
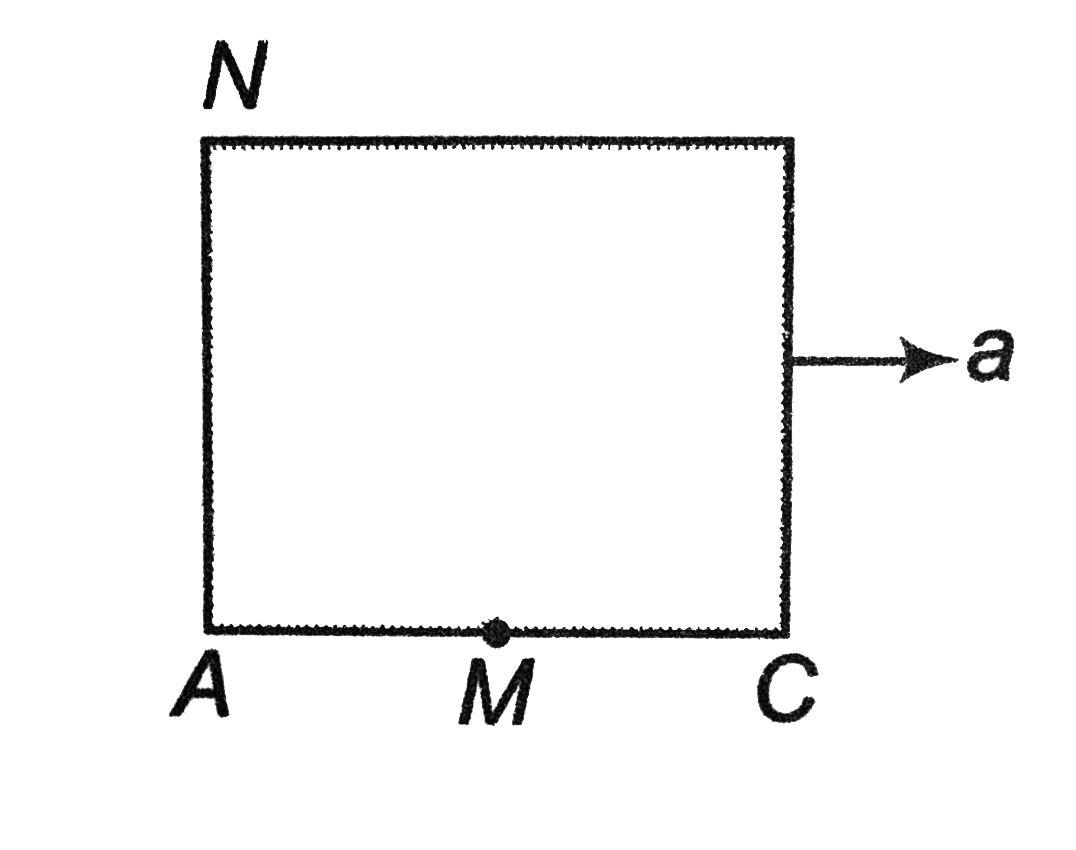
View SolutionA cubical closed vessel of side 5m filled with a liquid is accelerated with an acceleration a. Find the value of a so that pressure at mid pointM of AC is equal to pressure at N.
 .View Solution
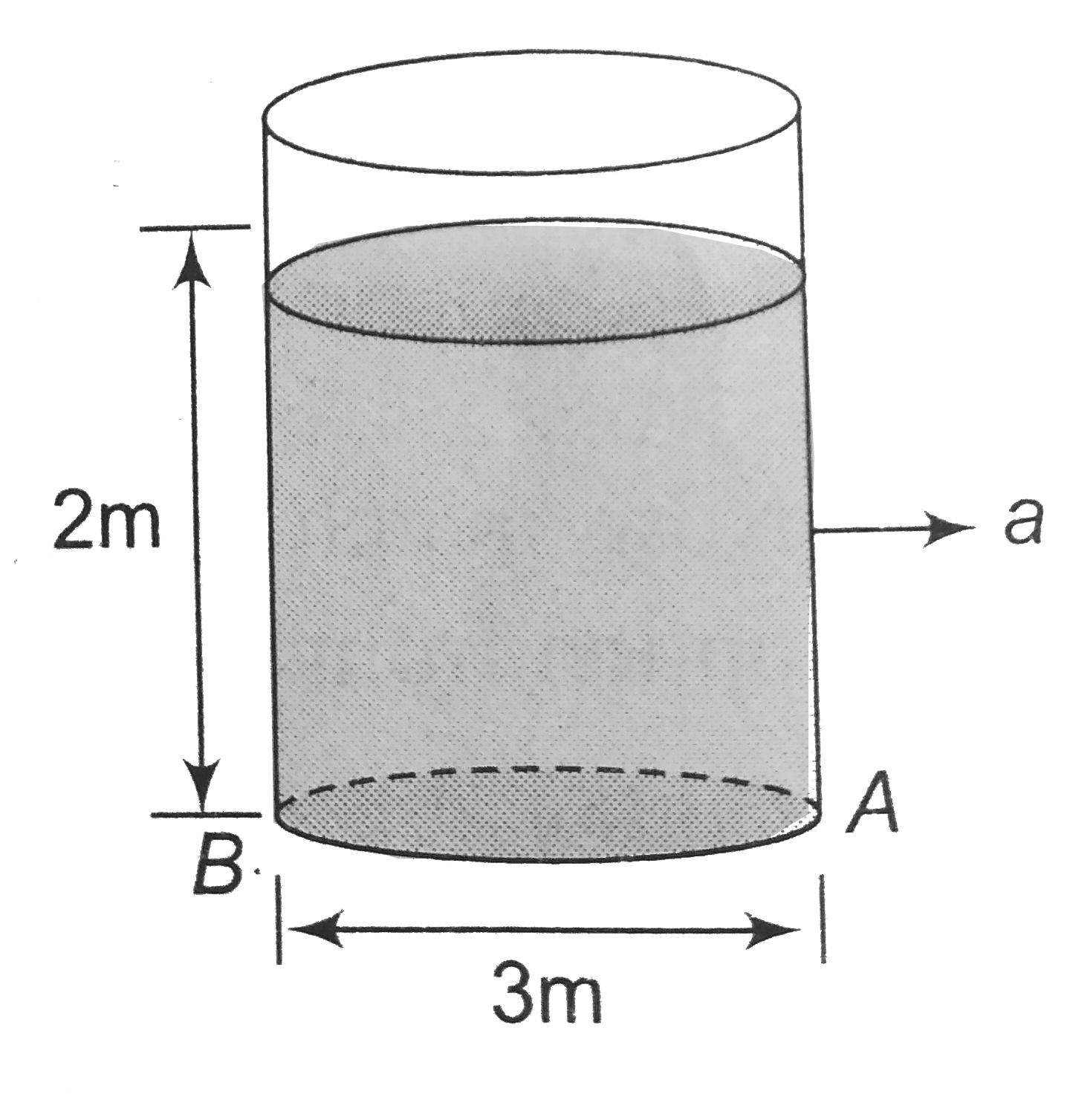
.View SolutionThe minimum horizontal acceleration of the container4 so that pressure at the point A of the container becomes atmospheric is (The tank is of sufficient height)
 View Solution
View SolutionThe minimum horizontal acceleration of the container a so that pressure at the point A of the container becomes atmospheric is (The tank is of sufficient height)
 View Solution
View SolutionA metal sphere connected by a string is dipped in a liquid of density ρ as shown in figure. The pressure at the bottom of the vessel will be, (p0=atmospheric pressure )
 View Solution
View Solution_S01_057_Q01.png)
A liquid of density ρ is filled in a U-tube, whose one end is open & at the other end a bulb is fitted whose pressure is PA. Now this tube is moved horizontally with acceleration a as shown in the figure. during motion it is found that liquid in both column is at same level at equilibrium if atmospheric pressure is P0 then value of PA isView Solution