A film of soap solution is trapped between a vertical frame and a light wire ab of length 0.1 m. If g=10m/s2 , then the load mass that should be suspended from the wire to keep it in equilibrium is : (σ=25×10−3N/m)
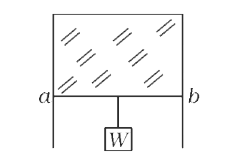
(a)0.25 gm
(b)0.3 gm
(c)0.4 gm
(d)0.5 gm
The correct Answer is:D
Force balancing, ¯¯¯w=2σl,m×10=2×25×10−3×0.1,m=0.5g
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - LEVEL -250videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE MAIN (LEVEL - 1 )31videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - LEVEL-0 ( Short Answer Type - II )15videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE53videos
LAWS OF MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)78videos
MAGNETIC EFFECTS OF CURRENT
Similar Questions
A light wire AB of length 10 cm can slide on a vertical frame as shown in figure. There is a film of soap solution trapped between the frame and the wire. Find the load W that should be suspended from the wire to keep it in equilibrium. Neglect friction. Surface tension of soat solution =25 dyne cm−1. Take g=10ms−2
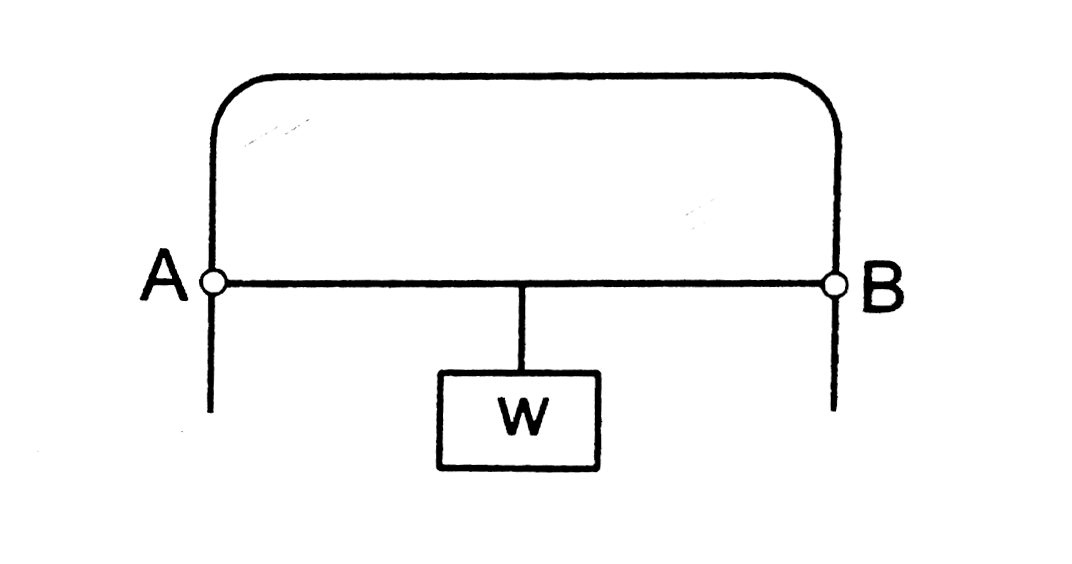View SolutionA soap film of surface tension 3×10−2N/m formed in a rectangular frame can support a straw as shown in Fig. If g=10ms−2, the mass of the straw is
View Solution
Knowledge Check
- Question 1 - Select One
A uniform wire of length 20 m and weighing 5 kg hangs vertically. If g=10ms−2, then the speed of transverse waves in the middle of the wire is
A10ms−1B10√2ms−1C4ms−1D2ms−1
A load of 4kg is suspended from a ceiling through a steel wire of length 20m and radius 2mm. It is found that the length of the wire increases by 0.031mm, as equilibrium is achieved. If g=3.1×πms(−2), the value of young's modulus of the material of the wire (in Nm−2) is
View SolutionA wire of mass 5 gm is kept horizontally on the surface of water. What ist he minimum length of the wire so that it does not break the surface film.Surface tension =72×10−3N/m
View SolutionA metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
View Solution_E01_194_Q01.png)
PQRS is a rectangular frame of copper wire shown in figure the side RS of the frame is movable. If a soap film is formed on it then what is the diameter of the wire to maintain equilibirum (given surface tension of soap solution =0.045N/m and density of copper =8.96×103kg/m3)View SolutionA soap film in formed on a frame of area 4×10−3m2. If the area of the film in reduced to half, then the change in the potential energy of the film is (surface tension of soap solution=40×10−3N/m)
View SolutionA copper wire of negligible mass, 1m length and cross-sectional area 10−6m2 is kept on a smooth horizontal table with one end fixed. A ball of mass 1kg is attached to the other end. The wire and the ball are rotating with an angular velocity of 20rad/s. If the elongation in the wire is 10−3m.
a. Find the Young's modulus of the wire (in terms of ×1011N/m2).
b. If for the same wire as stated above, the angular velocity is increased to 100rad/s and the wire breaks down, find the breaking stress (in terms of ×1010N/m2).View SolutionA load of 4.0 kg is suspended from a ceiling through a steel wire of length 20 m and radius 2.0 mm. It is found that the length of the wire increases by 0.031 mm as equilibrium is achieved. Find Young modulus of steel. Take g=3.1πms−2
View Solution