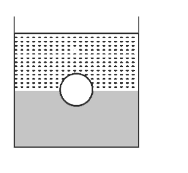
A solid uniform ball of volume V floats on the interface of two immiscible liquids (see the figure). The specific gravity of the upper liquid is ρ1 and that of lower one is ρ2 and the specific gravity of ball is ρ(ρ1<ρ<ρ2) The fraction of the volume of the ball in the upper liquid is:
The correct Answer is:0.8
Let V be the total volume of the ball and v be the volume of the ball in the upper liquid. Then V−v is the volume of the lower liquid displaced.

Using the law of floatation, we have
Vρg=vρ1g+(V−v)ρ2g,Vρ,vρ=vρ1+Vρ2,V(ρ−ρ2)=v(ρ1−ρ2),vV=ρ−ρ2ρ1−ρ2=ρ2−ρρ2−ρ1
Topper's Solved these Questions
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - LEVEL -2
50 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE MAIN (LEVEL - 1 )
31 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - LEVEL-0 ( Short Answer Type - II )
15 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)
78 Videos
Similar Questions
A solid uniform ball of volume V floats on the interface of two immiscible liquids (see the figure). The specific gravity of the upper liquid is ρ1 and that of lower one is ρ2 and the specific gravity of ball is ρ(ρ1>ρ>ρ2) The fraction of the volume the ball in the upper liquid is

View SolutionA solid uniform ball of volume V floats on the interface of two immiscible liquids (see the figure). The specific gravity of the upper liquid is ρ1 and that of lower one is ρ2 and the specific gravity of ball is ρ(ρ1>ρ>ρ2) The fraction of the volume the ball in the u of upper liquid is

View SolutionA solid uniform ball of volume V floats on the interface of two immiscible liquids [The specific gravity of the upper liquid is γ/2 and that of the lower liquid is 2γ, where γ is th especific gracity of the solid ball.] The fraction of the volume of the ball that will be in upper liquid is
View SolutionA solid uniform ball having volume V and density ρ floats at the interface of two unmixible liquids as shown in Fig. 7(CF).7. The densities of the upper and lower liquids are ρ1 and ρ2 respectively, such that ρ1<ρ<ρ2. What fractio9n of the volume of the ball will be in the lower liquid.

View SolutionA solid sphere having volume V and density ρ floats at the interface of two immiscible liquids of densites ρ1 and ρ2 respectively. If ρ1<ρ<ρ2, then the ratio of volume of the parts of the sphere in upper and lower liquid is
View SolutionA block of density ρ floats in a liquid with its one third volume immersed. The density of the liquid is
View SolutionA solid sphere of radius r is floating at the interface of two immiscible liquids of densities ρ1 and ρ2(ρ2>ρ1), half of its volume lying in each. The height of the upper liquid column from the interface of the two liquids is h. The force exerted on the sphere by the upper liquid is (atmospheric pressure =p0 and acceleration due to gravity is g):
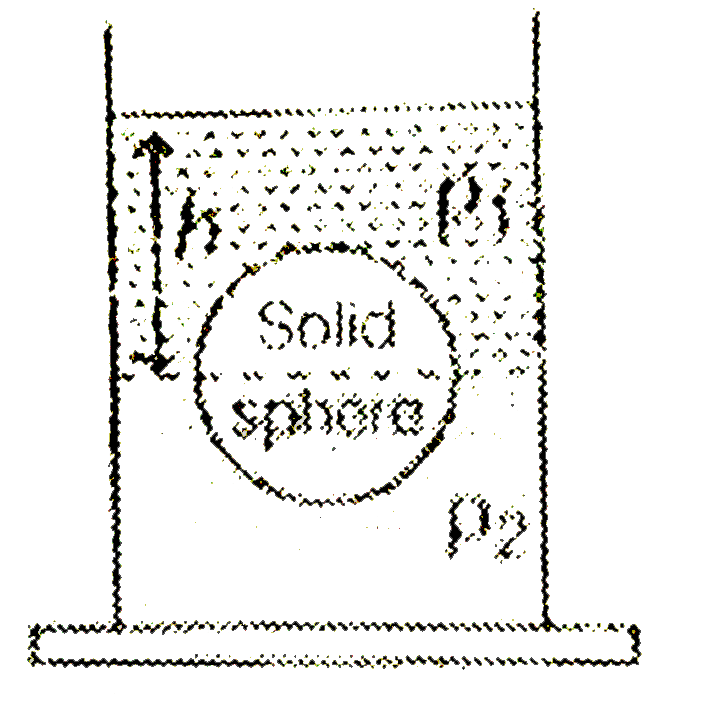
View SolutionWhen two substances of specific gravities d1 and d2 are mixed in equal volumes the specific garvity of mixture is found to be ρ1. When they are mixed in equal masses, the specific gravity of the mixture is found to be ρ2.(d1≠d2)
View SolutionA wide vessel with a small hole at the bottom is filled with two liquids. The density and height of one liquid are ρ1 and h1 and that of the other are ρ2 and h2(ρ1>ρ2). The velocity of liquid coming out of the hole is:
View SolutionWill an object of density ρ float in a fluid of density 1.5 ρ? If yes what fraction of the object's volume will remain above the fluid?
View Solution
