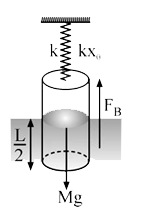
A uniform cylinder of length L and mass M having cross-sectional area A is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half submerged in a liquid of density σ at equilibrium position. The extension x0 of the spring when it is in equilibrium is:
Mgk(1−LAσM)
Mgk(1−LAσ2M)
Mgk(1+LAσM)
Mgk
The correct Answer is:B
Let x0 be the extension of the spring in equilibrium position. From FBD of cylinder in equilibrium,
Kx0+FB=Mg
kx0+σL2Ag=Mgx0=Mg−σLAg2k=Mgk(1−σLA2M)
Topper's Solved these Questions
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - LEVEL -2
50 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)
78 Videos
Similar Questions
A uniform cylinder of length (L) and mass (M) having cross sectional area (A) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half - submerged in a liquid of density (ρ) at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with small amplitude. If the force constant of the spring is (k), the frequency of oscillation of the cylinder is.
View SolutionA uniform cylinder of length (L) and mass (M) having cross sectional area (A) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half - submerged in a liquid of density (rho) at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with small amplitude. If the force constant of the spring is (k), the prequency of oscillation of the cylindcer is.
View SolutionA uniform cylinder of length (L) and mass (M) having cross sectional area (A) is suspended, with its length vertical, from a fixed point by a massless spring, such that it is half - submerged in a liquid of density (rho) at equilibrium position. When the cylinder is given a small downward push and released it starts oscillating vertically with small amplitude. If the force constant of the spring is (k), the prequency of oscillation of the cylindcer is.
View SolutionA block of known mass is suspended from a fixed support through a ligh spring. Can you find the time period of vertical oscillation only by measuring the extension of the spring when the block is in equilibrium?
View SolutionA rod of length l and mass m, pivoted at one end, is held by a spring at its mid - point and a spring at far end. The spring have spring constant k. Find the frequency of small oscillations about the equilibrium position.
View SolutionA block of density 2000kg/m3 and mass 10kg is suspended by a spring stiffness 100N/m. The other end of the spring is attached to a fixed support. The block is completely submerged in a liquid of density 1000kg/m3. If the block is in equilibrium position.
View SolutionA cube of mass m and density D is suspended from a point P by a spring of stiffness k. The system is kept inside a beaker filled with a liquid of density d. The elongation in the spring, assuming D>d, is :

View SolutionFigure shows a solid uniform cylinder of radius R and mass M, which is free to rotate about a fixed horizontal axis O and passes through centre of the cylinder. One end of an ideal spring of force constant k is fixed and the other end is higed to the cylinder at A. Distance OA is equal to R2. An inextensible thread is wrapped round the cylinder and passes over a smooth, small pulley. A block of equal mass M and having cross sectional area A is suspended from free end of the thread. The block is partially immersed in a non-viscous liquid of density ρ.
If in equilibrium, spring is horizontal and line OA is vertical, calculate frequency of small oscillations of the system.

View SolutionTwo wires have identical lengths and areas of cross-section are suspended by mass M. Their Young's modulus are in the ratio 2:5.
View Solutionwire of length I has a ear mass density λ and area of cross-section A and the Young's modulus y is suspended vertically from rigid support. The extension produced in wire due to its own weight
View Solution
