A wooden stick of length L, radius R and density ρ has a small metal piece of mass m ( of negligible volume) attached to its one end. Find the minimum value for the mass m (in terms of given parameters) that would make the stick float vertically in equilibrium in a liquid of density σ(>ρ).
The correct Answer is:πR2L(√ρσ−ρ)
πR2L(√ρσ−ρ)
Let M = Mass of stick = πR2ρL
I = immersed length of the rod
G = CM of rod B = centre of buoyant force (F)
C = CM of rod + mass (m)
YCM= Distance of C from bottom of the rod
Mass m should be attached to the lower end because otherwise B will be below G and C will be above G and the torque of the couple of two equal and opposite forces F and (M + m)g will be counter clockwise on displacing the rod leftwards. Therefore, the rod cannot be in rotational equilibrium. See the figure (iii). Now, refer figure (i) and (ii)
For vertical equilibrium Mg+mg=Fupthrustor(πR2L)ρg+mg=(πR2l)σg∴l=(πR2Lρ+mπR2σ)
Position of CM (of rod + m ) from bottom Ycm=M.L2M+m=(πR2Lρ)L2(πR2Lρ)+m
Centre of buoyancy (B) is at a height of l2 from the bottom.
We can see from figure (ii) that for rotational equilibrium of the rod, B should either lie above C or at the same level of B. Therefore, l2≥YCM
or πR2Lρ+m2πR2σ≥(πR2Lρ)L2(πR2Lρ)+morm+πR2Lρ≥πR2L√ρσorm≥πR2L(√ρσ−ρ)
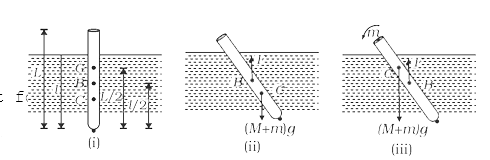
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE MAIN (LEVEL - 1 )31videos
LIQUIDS
- BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE53videos
LAWS OF MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)78videos
MAGNETIC EFFECTS OF CURRENT
Similar Questions
The linear density of a thin rod of length 1m lies as λ=(1+2x), where x is the distance from its one end. Find the distance of its center of mass from this end.
View SolutionA light rod of length l is pivoted at distance l/4 from the left end and has two masses m0 and m attached to its ends such that rod is in equilibrium. Find m in terms of m0.
 View Solution
View SolutionA rigid rod of mass m & length l is pivoted at one of its ends. If it is released from its horizontal position, find the speed of the centre of mass of the rod when it becomes vertical.
View SolutionA smooth chute is made in a dielectric sphere of radius R and uniform volume charge density. ρ. A charge particle of mass m and charge -q is placed at the centre of the sphere. Find the time period of motion of the particle?
 View Solution
View SolutionA solid sphere of radius R and density ρ is attached to one end of a mass-less spring of force constant k. The other end of the spring is connected to another solid sphere of radius R and density 3ρ. The complete arrangement is placed in a liquid of density 2ρ and is allowed to reach equilibrium. The correct statements(s) is (are)
View SolutionA solid sphere of radius R and density ρ is attached to one end of a mass-less spring of force constant k. The other end of the spring is connected to another solid sphere of radius R and density 3ρ. The complete arrangement is placed in a liquid of density 2ρ and is allowed to reach equilibrium. The correct statements(s) is (are)
View SolutionA mass m is taken to a height R from the surface of the earth and then is given a vertical velocity υ. Find the minimum value of υ, so that mass never returns to the surface of the earth. (Radius of earth is R and mass of the earth m).
View SolutionA needle of length l and density ρ will float on a liquid of surface tension σ if its radius r is less than or equal to:
View SolutionA rod of length L, cross sectional area A and density ρ is hanging from a rigid support by spring of stiffries k. A very small sphere of mass m is rigidly attached at the bottom of the rod. The rod is partially immersed in a liquid of density ρ. Find the period of small oscillations.
View SolutionA light rod length L, is hanging from the vertical smooth wall of a vehicle moving with acceleration √3g having a small mass attached at its one end is free to rotate about an axis passing through the other end. The minimum velocity given to the mass at its equilibrium position with respect to vehicle so that it can complete vertical circular motion respect to vehical) is √KgL. Find the value of K.
View Solution

