Assertion: The stream of water flowing at high speed from a garden hose pipe tends to spread like a fountain when held vertically up, but tends to narrow down when held vertically down.
Reason: In any steady flow of an incompressible fluid, the volume flow rate of the fluid remains constant.
Statement I is true, Statement II is true, Statement II is the correct explanation for Statement I.
Statement I is true, Statement II is true, Statement II is not the correct explanation for Statement I.
Statement I is true, Statement II is false
Statement I is false, Statement II is true.
The correct Answer is:A
From continuity equation, Av = constant
Topper's Solved these Questions
- LIQUIDSBook:VMC MODULES ENGLISHChapter:LIQUIDSExercise:JEE MAIN (LEVEL - 1 )
Explore 31 Videos
- LAWS OF MOTION Book:VMC MODULES ENGLISHChapter:LAWS OF MOTION Exercise:IMPECCABLE
Explore 53 Videos
- MAGNETIC EFFECTS OF CURRENT Book:VMC MODULES ENGLISHChapter:MAGNETIC EFFECTS OF CURRENT Exercise:JEE Advanced (Archive)
Explore 78 Videos
Similar Questions
STATEMENT-1: The stream of water flowing at high speed from a garden hose pipe tends to spread like a fountain when held vertically up, but tends to narrow down when held vertically down.
STATEMENT-2: In any steady flow of an incompressible fluid, the volume flow rate of the fluid remains constant.
View SolutionAssertion : When an ideal fluid flows through a pipe of non-uniform cross-section, then pressure is more at that section where area is more if the pipe is horizontal.
Reason : According to Bernoulli's theorem speed at broader cross-section will be less.
View Solution
Knowledge Check
Assertion: The flow of fluid is said to be steady if at any given point, the velocity of each passing fluid particle remains constant.
Reason: The path taken by a fluid particle under a steady flow is a streamline.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true and reason is false.DIf both assertion and reason are false.
When an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. Calculate the highest average speed that blood (ρ≈1000kg/m3) could have and still remain in laminar flow when it flows through the arorta (R=8×10−3m) Take the coeffiicient of viscosity of blood to be 4×10−3Pa−s
View SolutionWhen an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. What is the viscous force on a glass sphere of radius r=1mm falling through water (η=1×10−3Pa−s) when the sphere has speed of 3m/s?
View SolutionWhen an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. If the sphere in previous question has mass of 1×10−5kg what is its terminal velocity when falling through water? (η=1×10−3Pa−s)
A. 1.3m/s
B. 3.4m/s
C. 5.2m/s
D. 6.5m/s
View SolutionWhen an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. Which of the following may be concluded from the information in the passage?
View SolutionAssertion :− If you are squating down and sudenly get up, you can temporarilly feel light heated.
Reason :− Blood flows down from head when we suddenly rise.
View Solution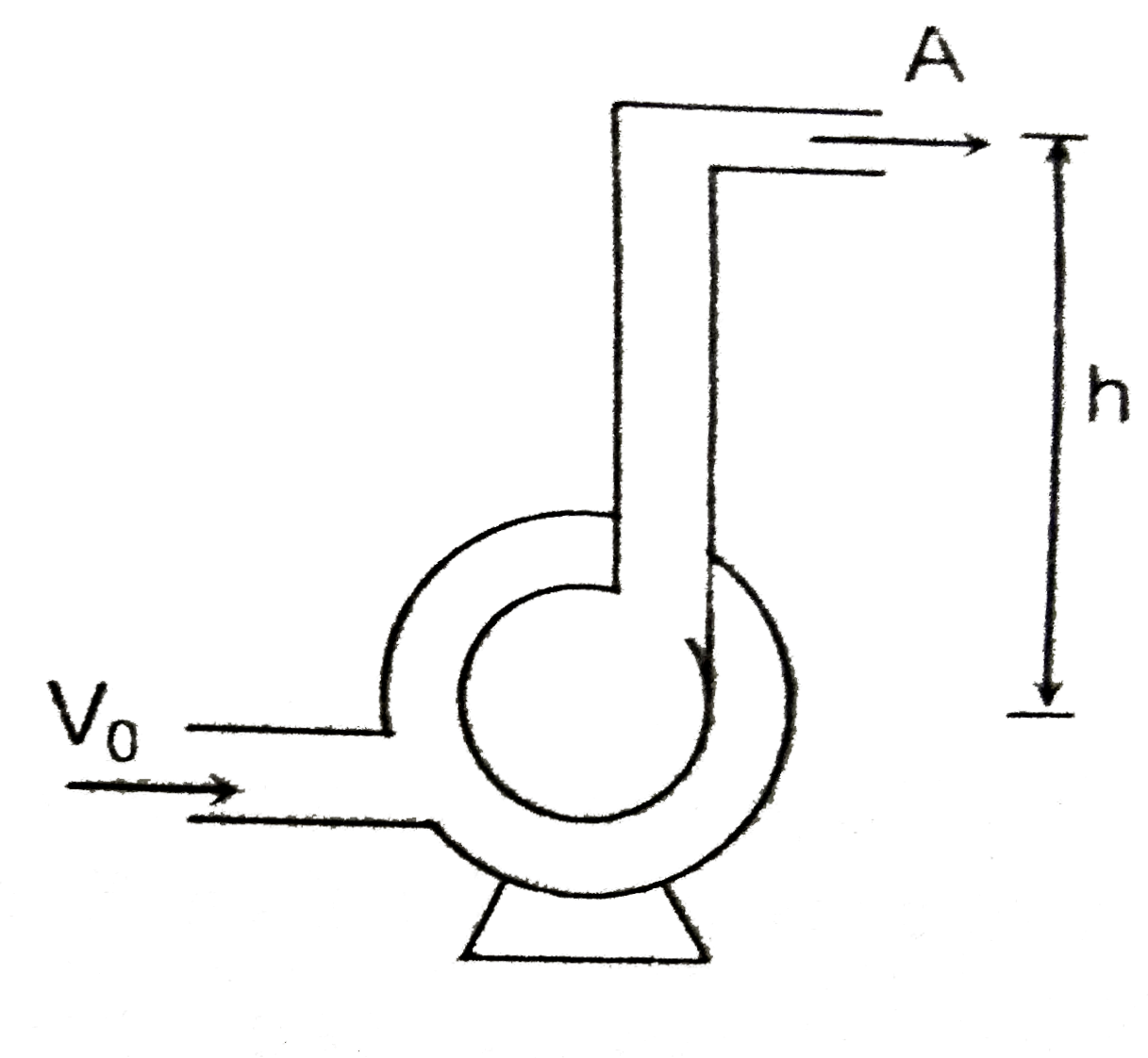
In a certain pump whose rated power is P. ideal fluid of denstiy ρ enters with speed V0 which lifts water upto height h through a pipe of uniform cross section area without discontinuity. Volumetric flow rate of the liquid is Q. Speed of fluid when it comes out of the pipe at point A is (Assume that pump works at 100 % efficiency and flow is streamline)
View SolutionWhen an object moves through a fluid, as when a ball falls through air or a glass sphere falls through water te fluid exerts a viscous foce F on the object this force tends to slow the object for a small sphere of radius r moving is given by stoke's law, Fw=6πηrv. in this formula η in the coefficient of viscosity of the fluid which is the proportionality constant that determines how much tangential force is required to move a fluid layer at a constant speed v, when the layer has an area A and is located a perpendicular distance z from and immobile surface. the magnitude of the force is given by F=ηAv/z. For a viscous fluid to move from location 2 to location 1 along 2 must exceed that at location 1, poiseuilles's law given the volumes flow rate Q that results from such a pressure difference P2−P1. The flow rate of expressed by the formula Q=πR4(P2−P1)8ηL poiseuille's law remains valid as long as the fluid flow is laminar. For a sfficiently high speed however the flow becomes turbulent flow is laminar as long as the reynolds number is less than approximately 2000. This number is given by the formula Re=2¯vρRη In which ¯v is the average speed ρ is the density η is the coefficient of viscosity of the fluid and R is the radius of the pipe. Take the density of water to be ρ=1000kg/m3
Q. Blood vessel is 0.10 m in length and has a radius of 1.5×10−3m blood flows at rate of 10−7m3/s through this vessel. The pressure difference that must be maintained in this flow between the two ends of the vessel is 20 Pa what is the viscosity sufficient of blood?
View Solution