a glass tube of length 133cm and of uniform cross-section is to be filled with mercury so that the volume of the unoccupied by mercury remains the same at all temperatures. If cubical coefficient for glass and mercury are respectively 0.000026/∘C and 0.000182/∘C , calculate the length of mercury column.
19 cm
133 cm
7 cm
None of these
The correct Answer is:A
To solve the problem of finding the length of the mercury column in a glass tube, we will follow these steps:
1. Understand the Problem: We have a glass tube of length L=133cm filled with mercury. The volume unoccupied by mercury must remain constant with temperature changes. This means that the change in volume of the mercury must equal the change in volume of the glass.
2. Define the Coefficients: The cubical expansion coefficients are given as:
- For glass, αG=0.000026°C−1
- For mercury, αM=0.000182°C−1
3. Volume Change Relations: The change in volume of the glass and mercury can be expressed as:
- Change in volume of glass: ΔVG=VG⋅αG⋅ΔT
- Change in volume of mercury: ΔVM=VM⋅αM⋅ΔT
Since the unoccupied volume remains constant, we set these two changes equal:
VG⋅αG⋅ΔT=VM⋅αM⋅ΔT
4. Initial Volumes: The initial volume of the mercury, VM, is given by:
VM=LM⋅A
where LM is the length of the mercury column and A is the cross-sectional area of the tube. The initial volume of the glass, VG, is given by:
VG=(L−LM)⋅A
5. Substituting Volumes: Substituting the expressions for VG and VM into the volume change equation gives:
(L−LM)⋅A⋅αG=LM⋅A⋅αM
6. Canceling Area: The cross-sectional area A cancels out from both sides:
(L−LM)⋅αG=LM⋅αM
7. Rearranging the Equation: Rearranging the equation gives:
L⋅αG−LM⋅αG=LM⋅αM
L⋅αG=LM⋅(αM+αG)
8. Solving for LM: Now, we can solve for LM:
LM=L⋅αGαM+αG
9. Substituting Values: Now we substitute the known values:
LM=133cm⋅0.0000260.000182+0.000026
10. Calculating the Denominator:
αM+αG=0.000182+0.000026=0.000208
11. Final Calculation:
LM=133⋅0.0000260.000208=0.0034580.000208≈16.6cm
12. Final Result: The length of the mercury column LM is approximately 16.6cm.
- For glass, αG=0.000026°C−1
- For mercury, αM=0.000182°C−1
- Change in volume of glass: ΔVG=VG⋅αG⋅ΔT
- Change in volume of mercury: ΔVM=VM⋅αM⋅ΔT
VG⋅αG⋅ΔT=VM⋅αM⋅ΔT
VM=LM⋅A
where LM is the length of the mercury column and A is the cross-sectional area of the tube. The initial volume of the glass, VG, is given by:
VG=(L−LM)⋅A
(L−LM)⋅A⋅αG=LM⋅A⋅αM
(L−LM)⋅αG=LM⋅αM
L⋅αG−LM⋅αG=LM⋅αM
L⋅αG=LM⋅(αM+αG)
LM=L⋅αGαM+αG
LM=133cm⋅0.0000260.000182+0.000026
αM+αG=0.000182+0.000026=0.000208
LM=133⋅0.0000260.000208=0.0034580.000208≈16.6cm
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Level -2
50 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Main (Archive) Level - 1
48 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
1 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K
10 Videos
- QUIZBOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS
30 Videos
Similar Questions
A glass bulb contains air and mercury. What fraction of the bulb must be occupied by mercury if the volume of air in the bulb is to remain constant at all temperatures? The coefficent of linear expansion of glass is 9×10−6/K.
View SolutionIn a mercury-glass thermometer the cross-section of the capillary portion is A0 and the volume of the bulb is V0 at 273K. If α and γ are the coefficients of linear and cubical expansion coefficients of glass and mercury respectively then length of mercury in the capillary at temperature t∘C is (Ignore the increase in cross-sectional area of capillary)
_E01_142_Q01.png)
View SolutionA glass vessel is filled up to 3/5th of its volume by mercury. If the volume expansivities of glass and mercury be 9×10−6/∘C and 18×10−5/∘C respectively, then the coefficient of apparent expansion of mercury is
View SolutionA column of mercury is in the middle of horizontal tube of uniform cross section closed at both ends. The pressure of the enclosed air column on either side of the mercury is 75 cm of mercury column. When the tuve is placed vertical the length air below the mercury column is 35 th of that above it. if length of mercury column is 10n cm. find n.
View SolutionTorricelli was the first do devise an experiment for measuring atmospheric pressure . He took calibrated hard glass tube , 1 m in lengt and of uniform cross section , closed at one end . He filled the whole tube with dry mercury taking care than no air or water droplets remain inside the tube , closed the opposite end of the tube tightly with thumb and inverted it . He put this inverted mercury tube into a mercury through , taking care that the end of the tube remains inside the mercury through , An interesting thing was noticed . Mercury in the tube fell down at first and then stopped at a particular position . The height was 76 cm above the free surface of mercury in the through . When the given tube was inclined or lowered in the mercury trough , the vertical haight of mercury level in the tube was always found constant .
Torricelli explained this by saying that the free surface of mercury in the trough . Hence , the hydrostatic pressure exerted by the trough measures the atmospheric pressure .
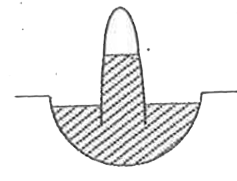
If this expriment uses water instead of mercury , then
A. length of water will be equal to 76 cm
B. length of water will be less than 76 cm
C. length of water will be greater than 76 cm
D. none of the above
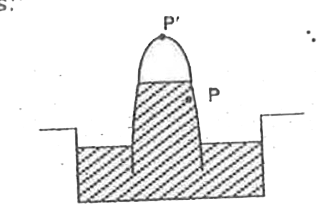
View SolutionTorricelli was the first do devise an experiment for measuring atmospheric pressure . He took calibrated hard glass tube , 1 m in lengt and of uniform cross section , closed at one end . He filled the whole tube with dry mercury taking care than no air or water droplets remain inside the tube , closed the opposite end of the tube tightly with thumb and inverted it . He put this inverted mercury tube into a mercury through , taking care that the end of the tube remains inside the mercury through , An interesting thing was noticed . Mercury in the tube fell down at first and then stopped at a particular position . The height was 76 cm above the free surface of mercury in the through . When the given tube was inclined or lowered in the mercury trough , the vertical haight of mercury level in the tube was always found constant .
Torricelli explained this by saying that the free surface of mercury in the trough . Hence , the hydrostatic pressure exerted by the trough measures the atmospheric pressure .
If an additional hole is also made at P ' at the top point of the tube , then

A. mercury will not come out of the tube
B. mercury may come out of the tube after some time .
C. mercury will come out of the tube instantly
D. none of these
View SolutionTorricelli was the first do devise an experiment for measuring atmospheric pressure . He took calibrated hard glass tube , 1 m in lengt and of uniform cross section , closed at one end . He filled the whole tube with dry mercury taking care than no air or water droplets remain inside the tube , closed the opposite end of the tube tightly with thumb and inverted it . He put this inverted mercury tube into a mercury through , taking care that the end of the tube remains inside the mercury through , An interesting thing was noticed . Mercury in the tube fell down at first and then stopped at a particular position . The height was 76 cm above the free surface of mercury in the through . When the given tube was inclined or lowered in the mercury trough , the vertical haight of mercury level in the tube was always found constant .
Torricelli explained this by saying that the free surface of mrcury in the trough . Hence , the hydrostatic pressure exerted by the trough measures the atmospheric pressure .

If a small hole is made at point P in the barometer tube , then
View SolutionThe mercury manometer consists if two unequal arms of equal cross section 1 cm^(2) and lenghths 100cm and 50cm. The two open ends are sealed with air in the tube at a pressure of 80cm of mercurey. Some amount of mercury is now introduced in the manometer through the stopcock connected to it. If mercury rises in the shorter tube to a lenght 10cm in steady state, find the length of the mercury column risen in the longer tube.
View SolutionThe volume of a glass vessel is 1000 cc at 20∘C. What volume of mercury should be poured into it at this temperature so that the volume of the remaining space does not change with temperature? Coefficients of cubical expansion of mercury and glass are 1.8×10−4C−1 and 9.0×10−6C−1. respectively.
View SolutionThe volume of a glass vessel is 1000 cc at 20∘C. What volume of mercury could be poured into it at this temperature so that the volume of the remaining space does not change with temperature? Coefficients of cubical expansion of mercury and glass are 1.8×10−4∘C−1 and 9×10−6∘C−1 respectively.
View Solution
