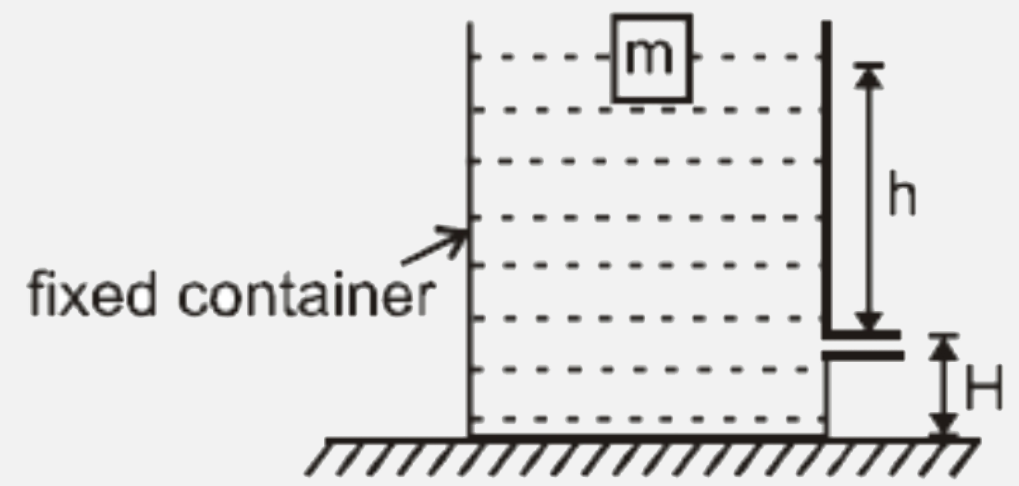
A solid sphere of radius R made of a material of bulk modulus B is surrounded by a liquid in a cylindrical container. A massless piston of area A (the area of container is also A) floats on the surface of the liquid. When a mass M is placed on the piston to compress the liquid , fractional change in radius of the sphere is MgαAB. Find the value of α.
The correct Answer is:9
Increase in pressure is Δp=MgA
Bulk modulus is B=ΔP(ΔV/V)
∴ΔVV=ΔPB=MgAB … (i)
Also, the volume of the sphere is
V=43πR3⇒ΔVV=3ΔRRorΔRR=13.ΔVV, using eq . (i) we get
ΔRR=Mg3AB∴n=9
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Level -2
50 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Main (Archive) Level - 1
48 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
1 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K
10 Videos
- QUIZBOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS
30 Videos
Similar Questions
A solid sphere of radius R made of a material of bulk modulus K is surrounded by a liquid in a cylindrical container. A massless pistion of area A floats on the surface of the liquid. When a mass M is placed on the piston to compress the liquid the fractional change in the radius of the sphere, δR/R, is .............
View SolutionThe radius of a sphere is √7cm. Find its curved surface area.
View Solution
Knowledge Check
A solid sphere of radius R made of a material of bulk modulus K is surrounded by a liquid in a cylindrical container. A massless piston of area A floats on the surface of the liquid. When a mass M is placed on the piston to compress the liquid the fractional change in the radius of the sphere, δR/R, is .............
AMg/2AKBMg/3AKCMg/AKD2Mg/3AKFind the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
A25MR2B65MR2C45MR2D75MR2
The bulk modulus for an incompresssible liquid is
View SolutionIf the pin hole in the container is very small compared to the area of the base of container and a block floats in the ideal liquid then, the speed of efflux is
View SolutionThe vapour pressure of a liquid in a closed container depends upon (1) temperature of liquid (2) quantity of liquid (3) surface area of the liquid
View SolutionA rubber ball of bulk modulus B is taken to a depth h of a liquid of density ρ. Find the fractional change in the radius of the ball.
View SolutionWhy does the liquid rise in a syringe when its piston is pulled up?
View SolutionFind the moment of inertia of a sphere about a tangent to the sphere, while the mass of the sphere is M and the radius of the sphere is R.
View Solution
