A conducting ring of mass 2 kg and radius 0.5 m is palced on a smooth horizationl plante . The ring carries a cuurent i=4A. A horizationtal magnetic field B=10 T is initinal angular acceleration of the ring will be

40∣∣rad/s2
20∣∣rad/s2
5∣∣rad/s2
15∣∣rad/s2
The correct Answer is:A
τ=Iα⇒MB=Iα⇒Iπr2B=12mr2α
α=2IBπm,α=2×4×10π2=40πrad/s2
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - LEVEL 2
50 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Main (Archive)
75 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - LEVEL 0 (LONG ANSWER TYPE )
3 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
- MOCK TEST 1BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 1EXERCISE - PART I : PHYSICS (SECTION-2)
10 Videos
Similar Questions
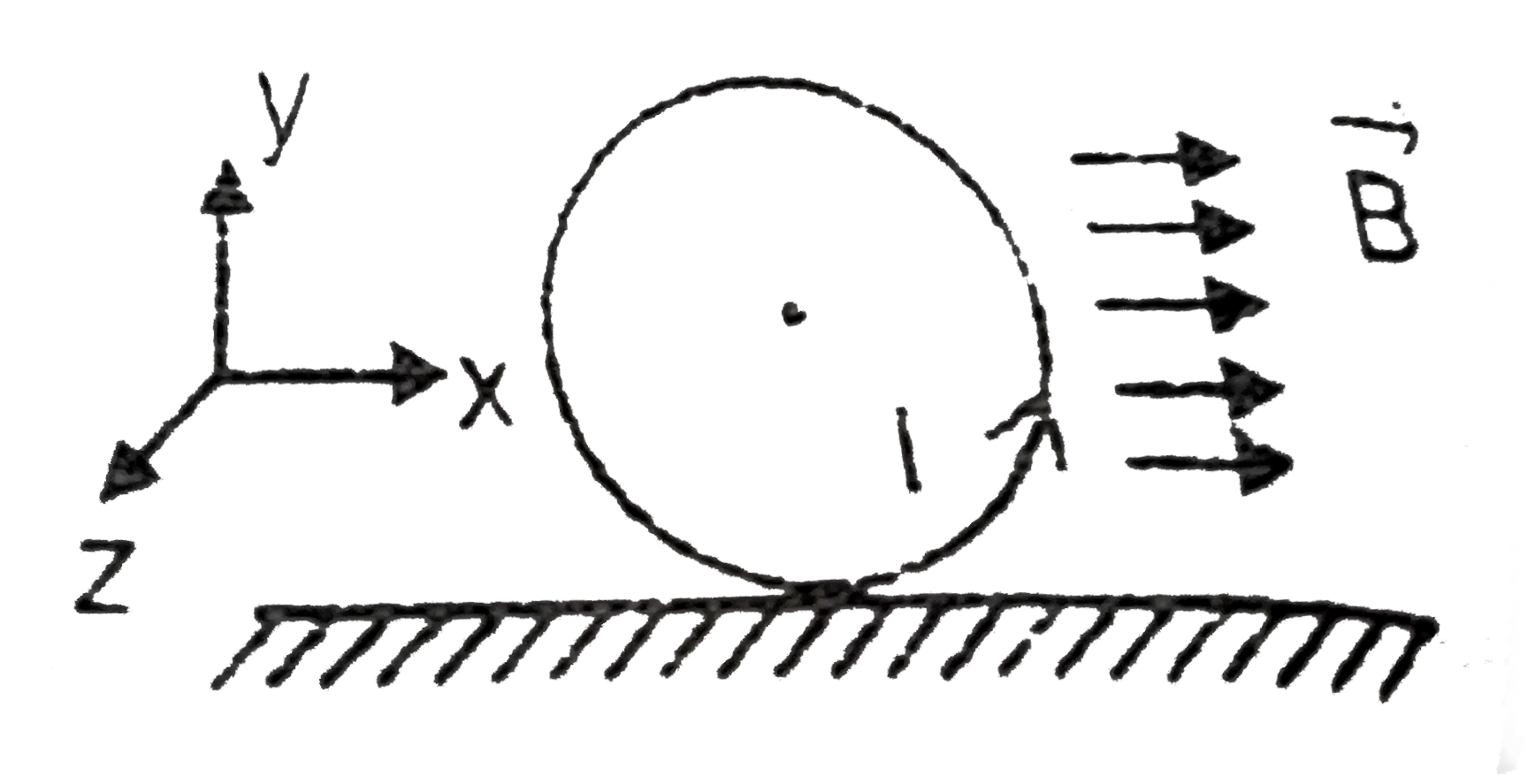
A conducting ring of mass 2kg and radius 0.5m is placed on a smooth plane. The ring carries a current of i=4A. A horizontal magnetic field B=10T is switched on at time t=0 as shown in fig The initial angular acceleration of the ring will be
 .
.
View SolutionA conducting ring of mass 2kg and radius 0.5m is placed on a smooth plane. The ring carries a current of i=4A. A horizontal magnetic field B=10T is switched on at time t=0 as shown in fig The initial angular acceleration of the ring will be
 .
.
View SolutionIn the shown figure a conducting ring of mass = 2kg and radius R = 0.5 m. lies on a smooth horizontal plane with its plane vertical. The ring carries a current of I=1πA. A horizontal uniform magnetic field of B = 12T is switched on at t =0. The initial angular acceleration α in rad/sec2 of the ring will be 4x if x is :
View SolutionA conducting ring of mass 2kg, radius 0.5m carries a current of 4A. It is placed on a smooth horizontal surface. When a horizontal magnetic field of 10 T parallel to the diameter of the ring is applied, the initial acceleration is (in rad/sec2)

View SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
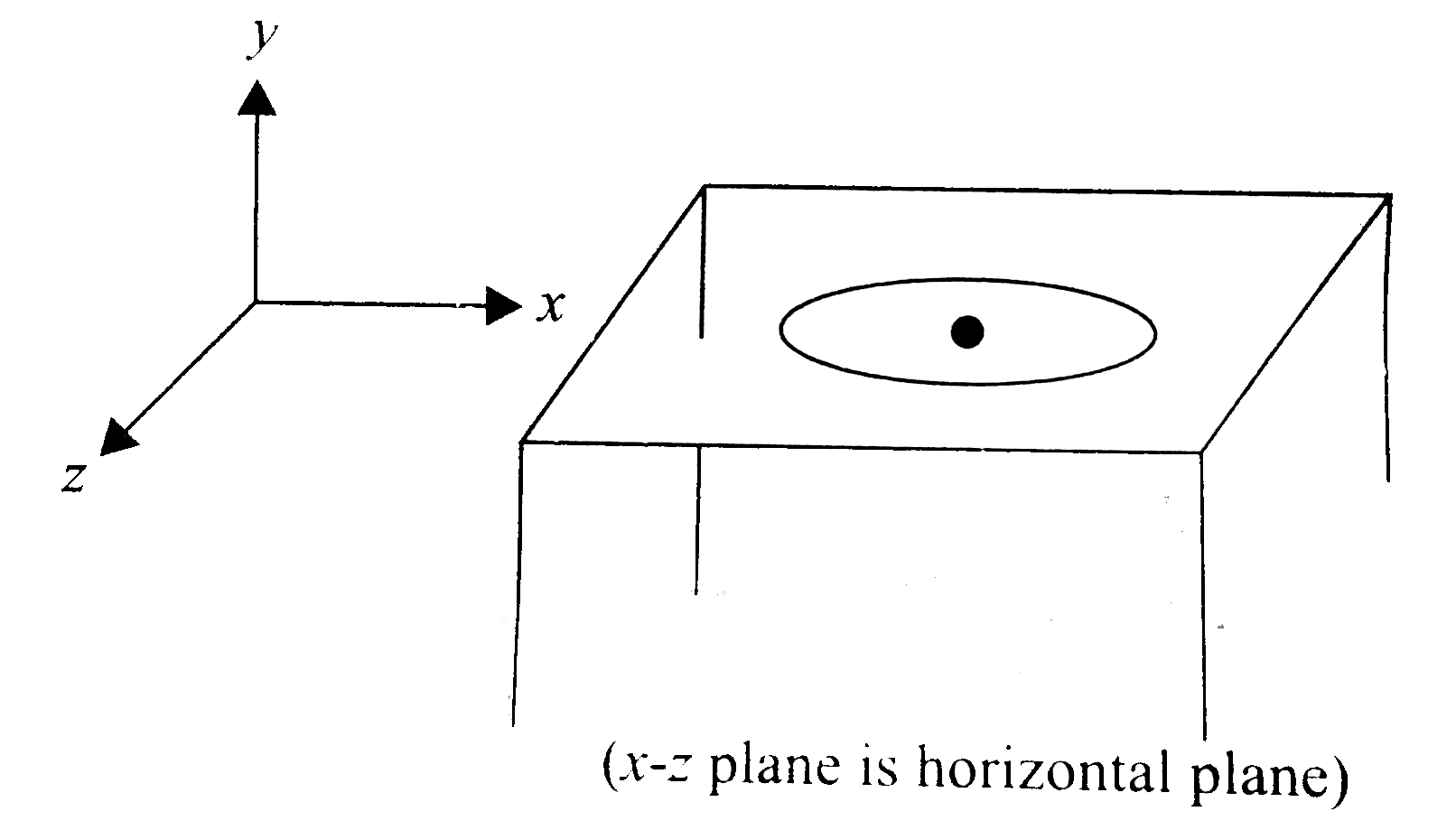
Heat generated (in kJ) through the ring till the instant when ring start toppling is
View SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
Net Induced EMF (in Volt) on conducting ring as function of time is
View SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then
Time (in second) at which ring start toppling is
View SolutionA uniform conducting ring of mass π kg and radius 1 m is kept on smooth horizontal table. A uniform but time varying magnetic field B=(ˆi+t2ˆj)T is present in the region, where t is time in seconds. Resistance of ring is 2(Ω). Then

Time (in second) at which ring start toppling is
View SolutionA uniformly conducting wire is bent to form a ring of mass 'm' and radius 'r', and the ring is placed on a rough horizontal surface with its plane horizontal. There exists a uniform and constant horizontal magnetic field of induction B. Now a charge q is passed through the ring in a very small time interval Δt. As a result the ring ultimately just becomes vertical. Calculate the value of g(acceleration due to gravity) in terms of other given quantities. Assume that friction is sufficient to prevent slipping and ignore any loss in energy.
View SolutionA smooth ring of mass m and radius R=1m is pulled at P with a constant acceleration a=4ms−2 on a horizontal surface such that the plane of the ring lies on the surface. Find the angular acceleration of the ring at the given position. (in rad/s2)
View Solution
