A current of 10 A flow around a closed path in a circuit which is in the horizontal plane as shown in the figure. The circuit consists of eight alternative arcs of radii r1=0.08m and r2=0.12m . Each subtends the same angle at the centre. If magnetic field at centre produced by this circuit is η×10−5T, then the value of η is ?
The correct Answer is:6.54
To solve the problem, we need to calculate the magnetic field at the center of a closed circuit consisting of eight alternating arcs of two different radii, r1=0.08m and r2=0.12m, with a current of I=10A flowing through it.
1. Understanding the Circuit Configuration:
The circuit consists of eight arcs, alternating between radius r1 and r2. Each arc subtends the same angle at the center.
2. Magnetic Field Contribution from Each Arc:
The magnetic field B at the center due to a circular arc of radius R carrying current I is given by the formula:
B=μ0Iθ4πR
where θ is the angle subtended by the arc in radians and μ0 is the permeability of free space, μ0=4π×10−7T m/A.
3. Calculating the Total Angle:
Since there are eight arcs, and each arc subtends the same angle, we can denote the angle subtended by each arc as θ. The total angle for all arcs is 8θ. For simplicity, we can assume each arc subtends π4 radians (which is 45∘), leading to:
8θ=2πradians(which is a full circle)
4. Magnetic Field Contribution from r1 and r2:
- For arcs of radius r1:
B1=μ0I⋅π44πr1=μ0I16r1
- For arcs of radius r2:
B2=μ0I⋅π44πr2=μ0I16r2
5. Total Magnetic Field at the Center:
Since there are four arcs of each radius, the total magnetic field B at the center is:
B=4B1+4B2=4(μ0I16r1)+4(μ0I16r2)
Simplifying this gives:
B=μ0I4(1r1+1r2)
6. Substituting the Values:
Plugging in the values:
B=(4π×10−7)⋅104(10.08+10.12)
7. Calculating the Terms:
- Calculate 10.08=12.5 and 10.12≈8.33.
- Therefore, 10.08+10.12=12.5+8.33=20.83.
8. Final Calculation:
B=(10−7⋅10⋅π)⋅20.83=6.54×10−5T
9. Finding η:
According to the question, the magnetic field at the center is given as η×10−5T. Thus, we have:
η=6.54
Final Answer:
η=6.54
The circuit consists of eight arcs, alternating between radius r1 and r2. Each arc subtends the same angle at the center.
The magnetic field B at the center due to a circular arc of radius R carrying current I is given by the formula:
B=μ0Iθ4πR
where θ is the angle subtended by the arc in radians and μ0 is the permeability of free space, μ0=4π×10−7T m/A.
Since there are eight arcs, and each arc subtends the same angle, we can denote the angle subtended by each arc as θ. The total angle for all arcs is 8θ. For simplicity, we can assume each arc subtends π4 radians (which is 45∘), leading to:
8θ=2πradians(which is a full circle)
- For arcs of radius r1:
B1=μ0I⋅π44πr1=μ0I16r1
- For arcs of radius r2:
B2=μ0I⋅π44πr2=μ0I16r2
Since there are four arcs of each radius, the total magnetic field B at the center is:
B=4B1+4B2=4(μ0I16r1)+4(μ0I16r2)
Simplifying this gives:
B=μ0I4(1r1+1r2)
Plugging in the values:
B=(4π×10−7)⋅104(10.08+10.12)
- Calculate 10.08=12.5 and 10.12≈8.33.
- Therefore, 10.08+10.12=12.5+8.33=20.83.
B=(10−7⋅10⋅π)⋅20.83=6.54×10−5T
According to the question, the magnetic field at the center is given as η×10−5T. Thus, we have:
η=6.54
η=6.54
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT Book:VMC MODULES ENGLISHChapter:MAGNETIC EFFECTS OF CURRENT Exercise:LEVEL 2
Explore 50 Videos
- MAGNETIC EFFECTS OF CURRENT Book:VMC MODULES ENGLISHChapter:MAGNETIC EFFECTS OF CURRENT Exercise:JEE Main (Archive)
Explore 75 Videos
- MAGNETIC EFFECTS OF CURRENT Book:VMC MODULES ENGLISHChapter:MAGNETIC EFFECTS OF CURRENT Exercise:LEVEL 0 (LONG ANSWER TYPE )
Explore 3 Videos
- LIQUIDSBook:VMC MODULES ENGLISHChapter:LIQUIDSExercise:JEE ADVANCED (LEVEL -2)
Explore 55 Videos
- MOCK TEST 1Book:VMC MODULES ENGLISHChapter:MOCK TEST 1Exercise:PART I : PHYSICS (SECTION-2)
Explore 10 Videos
Similar Questions
A current of 10A flows around a closed path in a circuit which is in the horizontal plane as shown in the figure. The circuit consists oi eight alternating arcs of radii r1=0.08m and r2=0.12m. Each subtends the same angle at the centre.
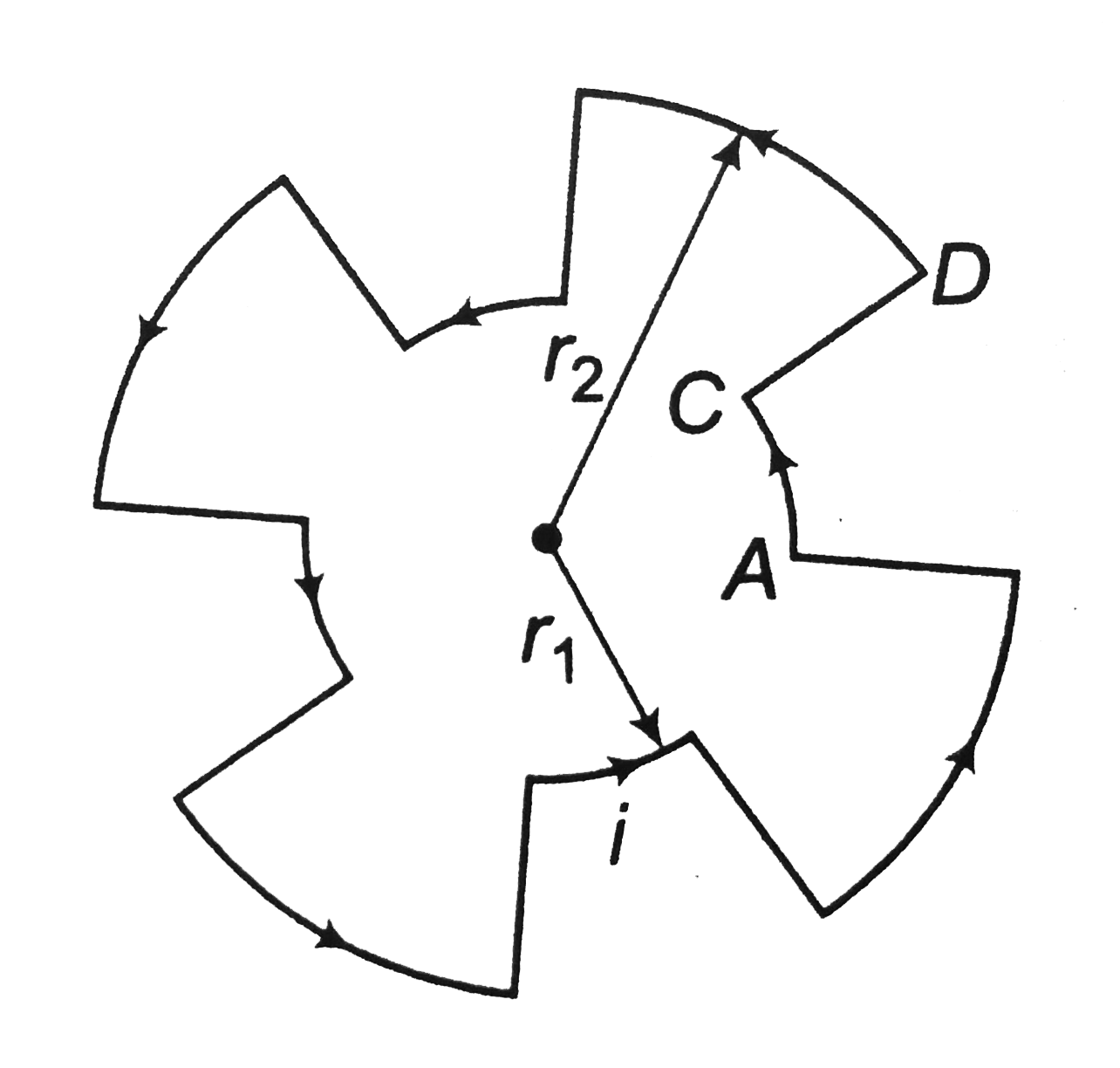
a. Find the magnetic field produced by this circuit at the centre.
b. An infinitely long straight wire carrying as current of 10A is passing through the centre of the above circuit vertically with the direction of the current being into the pane of the circuit. what is the force acting on the wire at the centre due to the current in the circuit? What is the force acting on the arc AC and the straight segment CD due to the current at the centre?
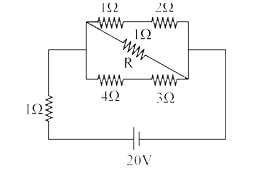
View SolutionFind the current through resistor R.
View SolutionIn the figure shown there are two semicircles of radii r1 and r2 in which a current i is flowing. The magnetic induction at the centre O will be

View SolutionIn the figure shown there are two semicircles of radii r1 and r2 in which a current i is flowing. The magnetic induction at the centre O will be

View SolutionIn the circuit shown in the figure , the alternating currents through inductor and capacitor are 1.2 and 1.0 A respectively . The current drawn from the generator is
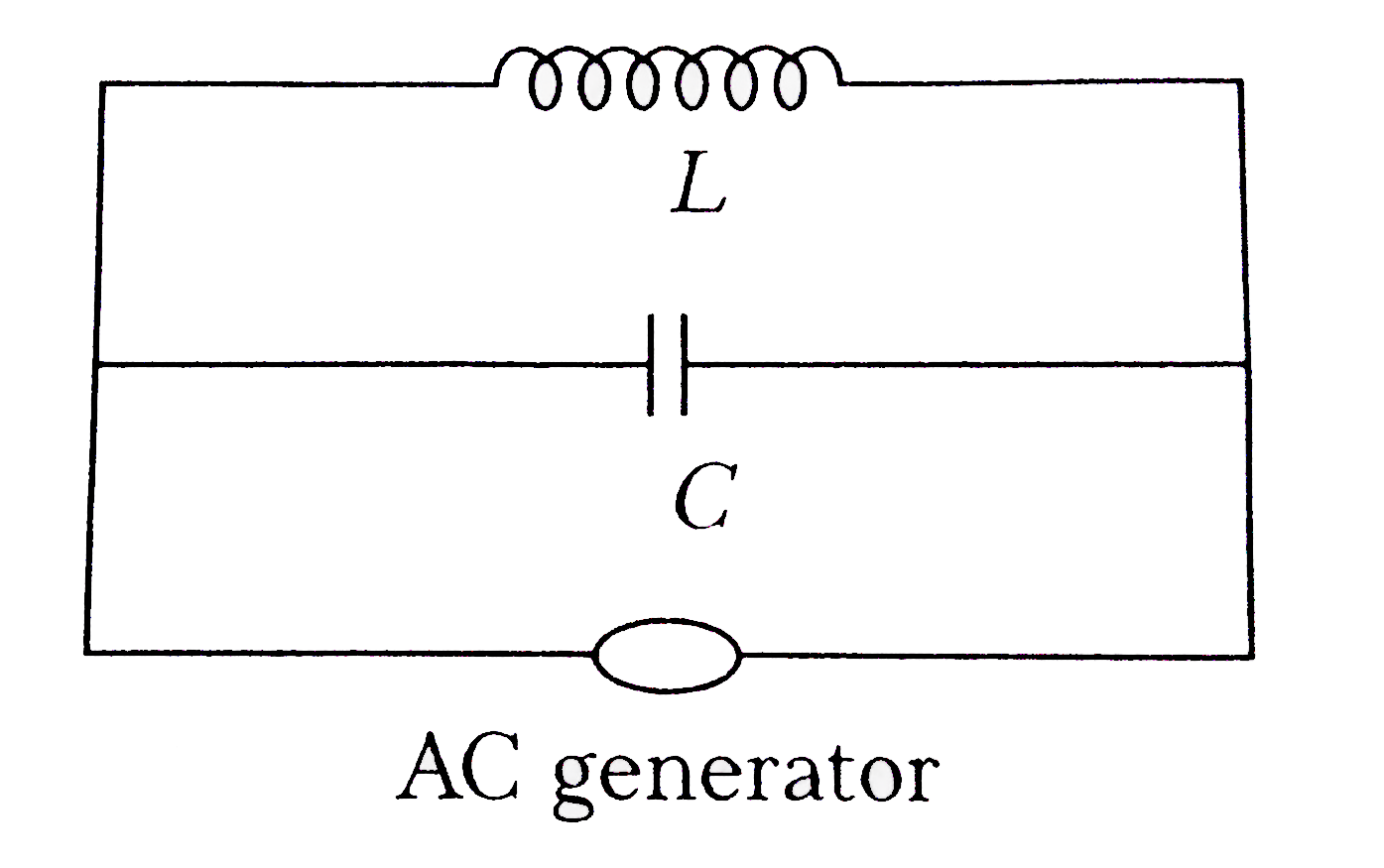
View SolutionA current of 2 A is made to flow through a coil which has only one turn. The magnetic field produced at the centre is4π×10−6Wb/m2. the radius of the coil is
View SolutionA solenoid of length 0.4m and diameter 0.6m consists of a single layer of 1000 turns of fine wire carrying a current of 5.0×10−3 ampere.The magnetic field strength on the axis at the middle is πN×10−5T, then find value of N.
View SolutionIn Fig. infinite conducting rings each having current i in the direciton shown are placed concentrically in the same plane as shown in the figure. The radii of rings are r,2r,22r,23r,......,(∞). The magnetic field at the centre of rings will be

View SolutionIn Fig. infinite conducting rings each having current i in the direciton shown are placed concentrically in the same plane as shown in the figure. The radii of rings are r,2r,22r,23r,......,(∞). The magnetic field at the centre of rings will be

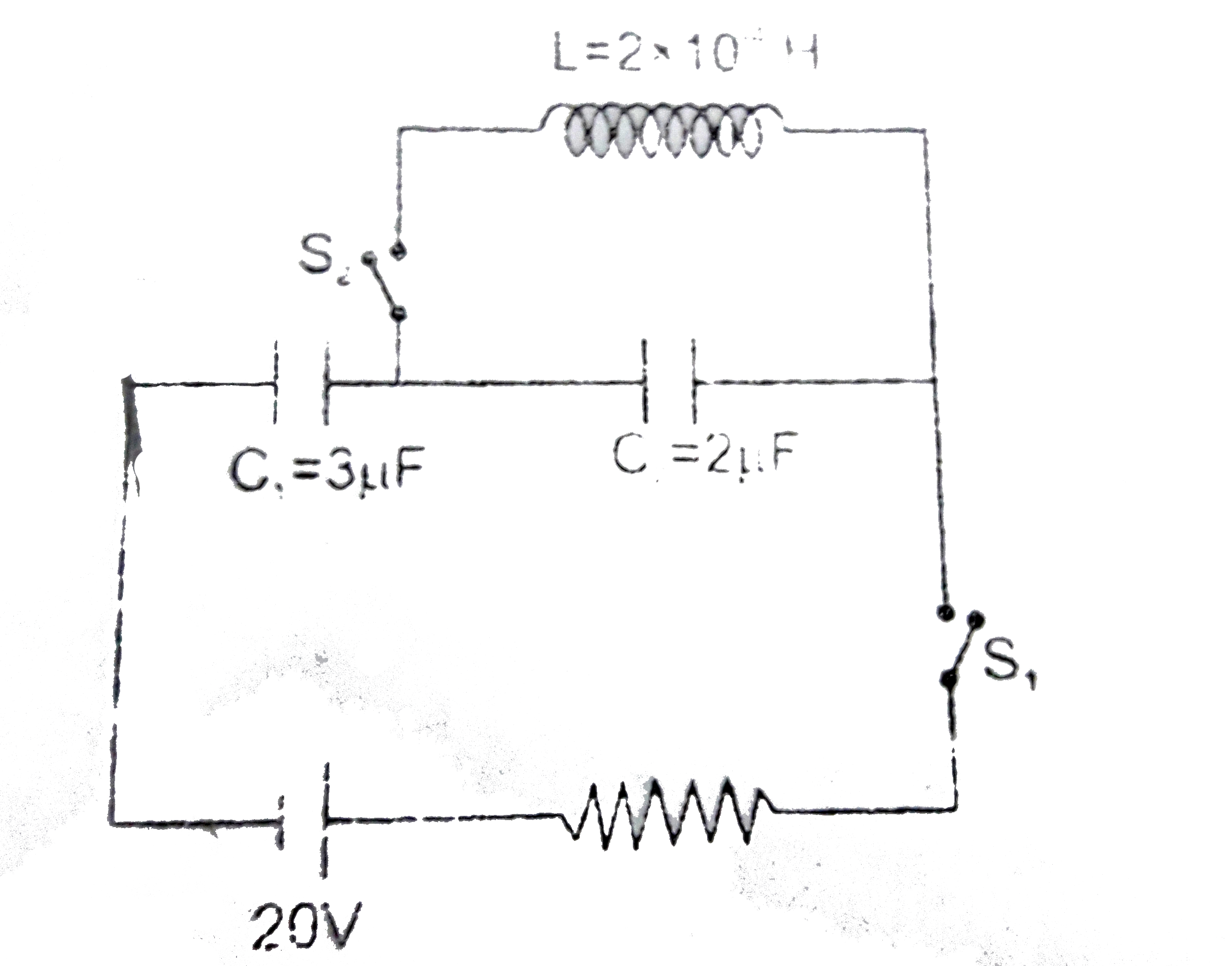
View SolutionThe circuit shown in figure is in the steady state with switch S1 closed.At t=0,S1 is opened and switch S2 is closed. The first instant t when energy in inductor becomes one third of that in capacitor is equal to π×10−5xsec. Then finout value of x.
View Solution