A uniformly conducting wire is bent to form a ring of mass 'm' and radius 'r', and the ring is placed on a rough horizontal surface with its plane horizontal. There exists a uniform and constant horizontal magnetic field of induction B. Now a charge q is passed through the ring in a very small time interval Δt. As a result the ring ultimately just becomes vertical. Calculate the value of g(acceleration due to gravity) in terms of other given quantities. Assume that friction is sufficient to prevent slipping and ignore any loss in energy.
To solve the problem, we will analyze the dynamics of the conducting ring when a charge is passed through it in a magnetic field. We will derive the expression for the acceleration due to gravity g in terms of the other given quantities.
1. Understanding the System:
- We have a conducting ring of mass m and radius r placed on a rough horizontal surface.
- A uniform magnetic field B is present, and a charge q is passed through the ring in a very short time interval Δt.
- The ring initially lies flat (horizontal) and then rotates to become vertical.
2. Torque Calculation:
- The torque τ acting on the ring due to the magnetic field can be expressed as:
τ=m⋅B
- The area vector A of the ring is given by A=πr2, and the magnetic moment m is related to the current I flowing through the ring:
m=I⋅A=I⋅πr2
3. Current Calculation:
- The current I can be expressed in terms of the charge q passed through the ring and the time interval Δt:
I=qΔt
4. Substituting Current into Torque:
- Substitute I into the torque equation:
τ=(qΔt)⋅πr2⋅B
5. Angular Momentum:
- The torque is also related to the change in angular momentum L:
τ=dLdt
- Integrating over the time interval gives:
L=τ⋅Δt
6. Change in Height:
- When the ring becomes vertical, its center of mass rises by a height r. The change in potential energy ΔU is given by:
ΔU=m⋅g⋅r
7. Equating Energies:
- The change in kinetic energy ΔK must equal the change in potential energy:
ΔK=ΔU
- Since the ring starts from rest, we can express the kinetic energy in terms of angular momentum:
L22I=m⋅g⋅r
8. Moment of Inertia:
- The moment of inertia I of the ring about its center is:
I=12mr2
- Using the parallel axis theorem, the effective moment of inertia when the ring rotates about the point of contact is:
I=12mr2+mr2=32mr2
9. Final Equation:
- Substitute L and I back into the energy equation:
(q⋅πr2BΔtΔt)22⋅32mr2=m⋅g⋅r
- Simplifying gives:
q2π2r4B23mr2=m⋅g⋅r
- Rearranging to solve for g:
g=q2π2r2B23m
Final Result:
g=q2π2r2B23m
- We have a conducting ring of mass m and radius r placed on a rough horizontal surface.
- A uniform magnetic field B is present, and a charge q is passed through the ring in a very short time interval Δt.
- The ring initially lies flat (horizontal) and then rotates to become vertical.
- The torque τ acting on the ring due to the magnetic field can be expressed as:
τ=m⋅B
- The area vector A of the ring is given by A=πr2, and the magnetic moment m is related to the current I flowing through the ring:
m=I⋅A=I⋅πr2
- The current I can be expressed in terms of the charge q passed through the ring and the time interval Δt:
I=qΔt
- Substitute I into the torque equation:
τ=(qΔt)⋅πr2⋅B
- The torque is also related to the change in angular momentum L:
τ=dLdt
- Integrating over the time interval gives:
L=τ⋅Δt
- When the ring becomes vertical, its center of mass rises by a height r. The change in potential energy ΔU is given by:
ΔU=m⋅g⋅r
- The change in kinetic energy ΔK must equal the change in potential energy:
ΔK=ΔU
- Since the ring starts from rest, we can express the kinetic energy in terms of angular momentum:
L22I=m⋅g⋅r
- The moment of inertia I of the ring about its center is:
I=12mr2
- Using the parallel axis theorem, the effective moment of inertia when the ring rotates about the point of contact is:
I=12mr2+mr2=32mr2
- Substitute L and I back into the energy equation:
(q⋅πr2BΔtΔt)22⋅32mr2=m⋅g⋅r
- Simplifying gives:
q2π2r4B23mr2=m⋅g⋅r
- Rearranging to solve for g:
g=q2π2r2B23m
g=q2π2r2B23m
Similar Questions
A force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:

View SolutionA ring of mass m and radius R rolls on a horizontal roudh surface without slipping due to an applied force 'F'. The frcition force acting on ring is :−

View Solution
Knowledge Check
A conducting ring is placed in a uniform magnetic field with its plane perpendicular to the field . An emf is induced in the ring if
Ait is rotated about its axis.Bit is rotated about its diameter.Cit is not moved.Dit is given translational motion in the field.
An impulse J is applied on a ring of mass m along a line passing through its centre O. The ring is placed on a rough horizontal surface. The linear velocity of centre of ring once it starts rolling without slipping is
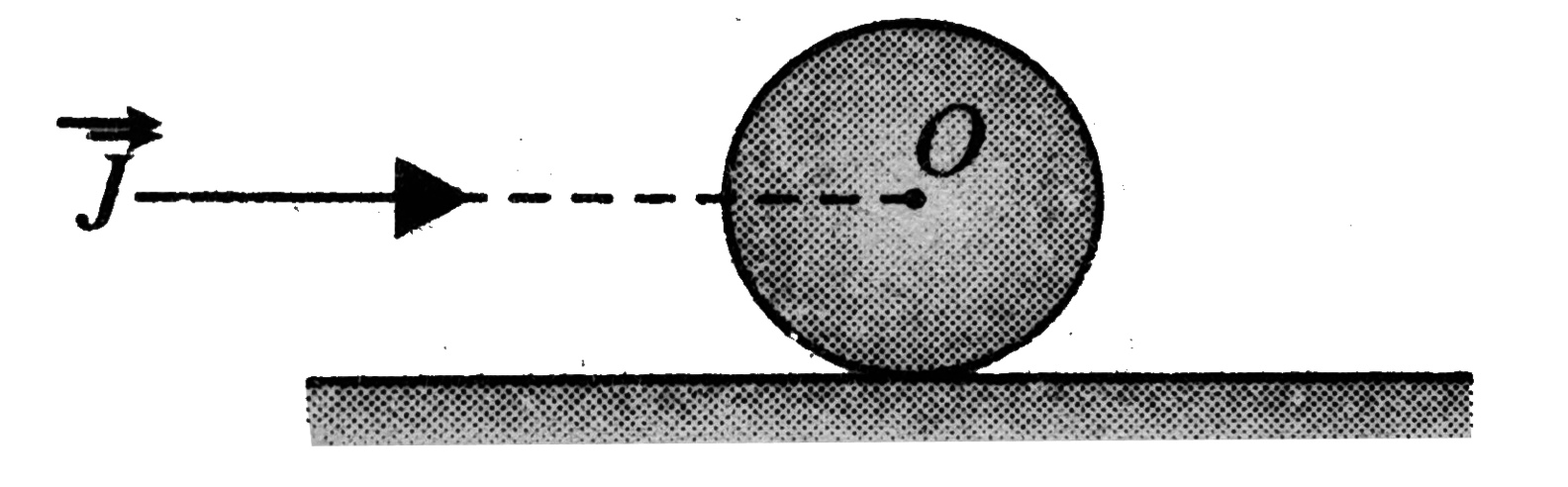
View SolutionA force (F=Mg) is applied on the top of a circular ring of mass M and radius R kept on a rough horizontal surface. If the ring rolls without slipping, then minimum coefficient of friction required is
_PHY_E05_236_Q01.png)
View SolutionA thin wire is bent in the form of a ring of diameter 3.0cm.The ring is placed horizontally on the surface of soap solution and then raised up slowly. Upward force necessary to break the vertical film formed between the ring and the solution is
View SolutionA metal ring of mass m and radius R is placed on a smooth horizontal table and is set rotating about its own axis in such a way that each part of the ring moves with a speed v. Find the tension in the ring.
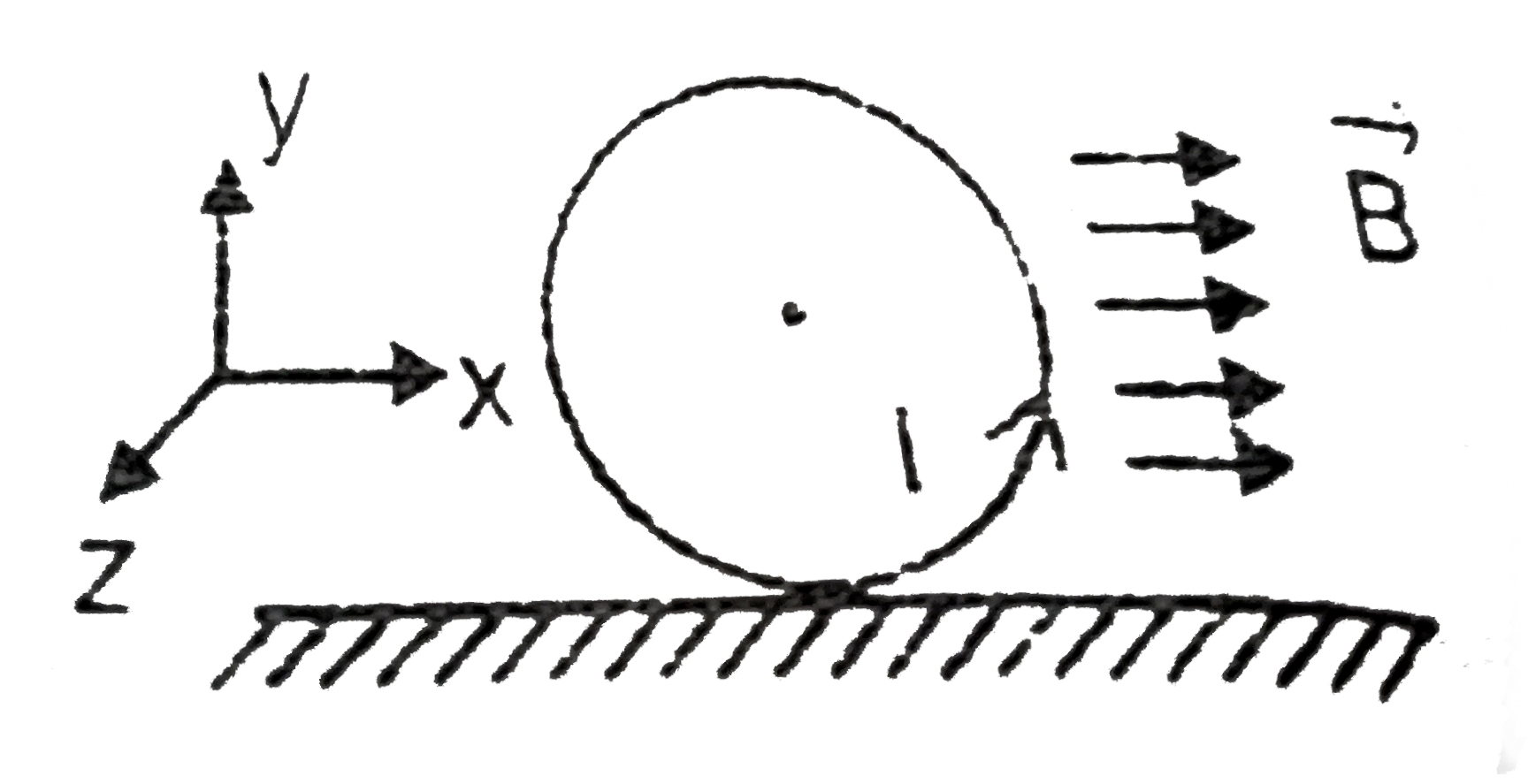
View SolutionIn the shown figure a conducting ring of mass = 2kg and radius R = 0.5 m. lies on a smooth horizontal plane with its plane vertical. The ring carries a current of I=1πA. A horizontal uniform magnetic field of B = 12T is switched on at t =0. The initial angular acceleration α in rad/sec2 of the ring will be 4x if x is :
View SolutionA ring of radius R is rolling on a horizontal plane with constant velocity v. There is a constant and uniform magnetic field B which is perpendicular to the plane of the ring. Emf across the lowest point A and right-most point C as shown in the figure will

View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring.

View Solution
