A kettle containing 1kg of water is heated open to atmosphere until evaporation is complete. The work done during this process is
The correct Answer is:172.28
To solve the problem of calculating the work done during the evaporation of 1 kg of water in a kettle heated open to the atmosphere, we can follow these steps:
1. Understand the Process:
- The process involves heating 1 kg of water until it completely evaporates. This is an open system where the water turns from liquid to gas.
2. Identify the Work Done Formula:
- The work done (W) during expansion against the atmospheric pressure can be calculated using the formula:
W=−PexternalΔV
- Here, Pexternal is the external pressure (atmospheric pressure), and ΔV is the change in volume.
3. Determine the Change in Volume:
- The change in volume (ΔV) when water evaporates can be expressed as:
ΔV=Vgas−Vliquid
- Since the volume of gas is significantly larger than the volume of liquid, we can approximate:
ΔV≈Vgas
4. Calculate the Volume of Gas:
- Using the Ideal Gas Law, we can express the volume of gas as:
PV=nRT
- Rearranging gives:
V=nRTP
5. Determine the Number of Moles (n):
- For 1 kg of water, the number of moles n is calculated as:
n=massmolar mass=1000 g18 g/mol≈55.56 mol
6. Substitute Values:
- Use R=8.314 J/(mol K), T=373 K (the boiling point of water), and P≈101325 Pa (atmospheric pressure).
- Substitute these values into the volume equation:
Vgas=(55.56 mol)(8.314 J/(mol K))(373 K)101325 Pa
7. Calculate the Volume:
- Performing the calculation:
Vgas≈(55.56)(8.314)(373)101325≈1.72 m3
8. Calculate Work Done:
- Now, substitute Vgas back into the work done formula:
W=−PexternalVgas≈−101325 Pa×1.72 m3≈−174,000 J
- Since we are interested in the magnitude of work done:
W≈174,000 J
Final Answer:
The work done during the evaporation of 1 kg of water is approximately 174,000 Joules.
- The process involves heating 1 kg of water until it completely evaporates. This is an open system where the water turns from liquid to gas.
- The work done (W) during expansion against the atmospheric pressure can be calculated using the formula:
W=−PexternalΔV
- Here, Pexternal is the external pressure (atmospheric pressure), and ΔV is the change in volume.
- The change in volume (ΔV) when water evaporates can be expressed as:
ΔV=Vgas−Vliquid
- Since the volume of gas is significantly larger than the volume of liquid, we can approximate:
ΔV≈Vgas
- Using the Ideal Gas Law, we can express the volume of gas as:
PV=nRT
- Rearranging gives:
V=nRTP
- For 1 kg of water, the number of moles n is calculated as:
n=massmolar mass=1000 g18 g/mol≈55.56 mol
- Use R=8.314 J/(mol K), T=373 K (the boiling point of water), and P≈101325 Pa (atmospheric pressure).
- Substitute these values into the volume equation:
Vgas=(55.56 mol)(8.314 J/(mol K))(373 K)101325 Pa
- Performing the calculation:
Vgas≈(55.56)(8.314)(373)101325≈1.72 m3
- Now, substitute Vgas back into the work done formula:
W=−PexternalVgas≈−101325 Pa×1.72 m3≈−174,000 J
- Since we are interested in the magnitude of work done:
W≈174,000 J
The work done during the evaporation of 1 kg of water is approximately 174,000 Joules.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - JEE (MAIN ARCHIVE)
32 Videos
- THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE)
44 Videos
- THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - LEVEL-2
50 Videos
- THERMOCHEMISTRYBOOK - VMC MODULES ENGLISHCHAPTER - THERMOCHEMISTRYEXERCISE - JEE ADVANCED (ARCHIVE)
31 Videos
- THERMODYNAMICS & THERMOCHEMISTRYBOOK - VMC MODULES ENGLISHCHAPTER - THERMODYNAMICS & THERMOCHEMISTRYEXERCISE - Impeccable
48 Videos
Similar Questions
Knowledge Check
An ideal gas system undergoes an isothermal process, then the work done during the process is
AnRTln(V2V1)BnRTln(V1V2)C2nRTln(V2V1)D2nRTln(V1V2)A cyclic process is shown in the figure. Work done during the cyclic process ABCDA is
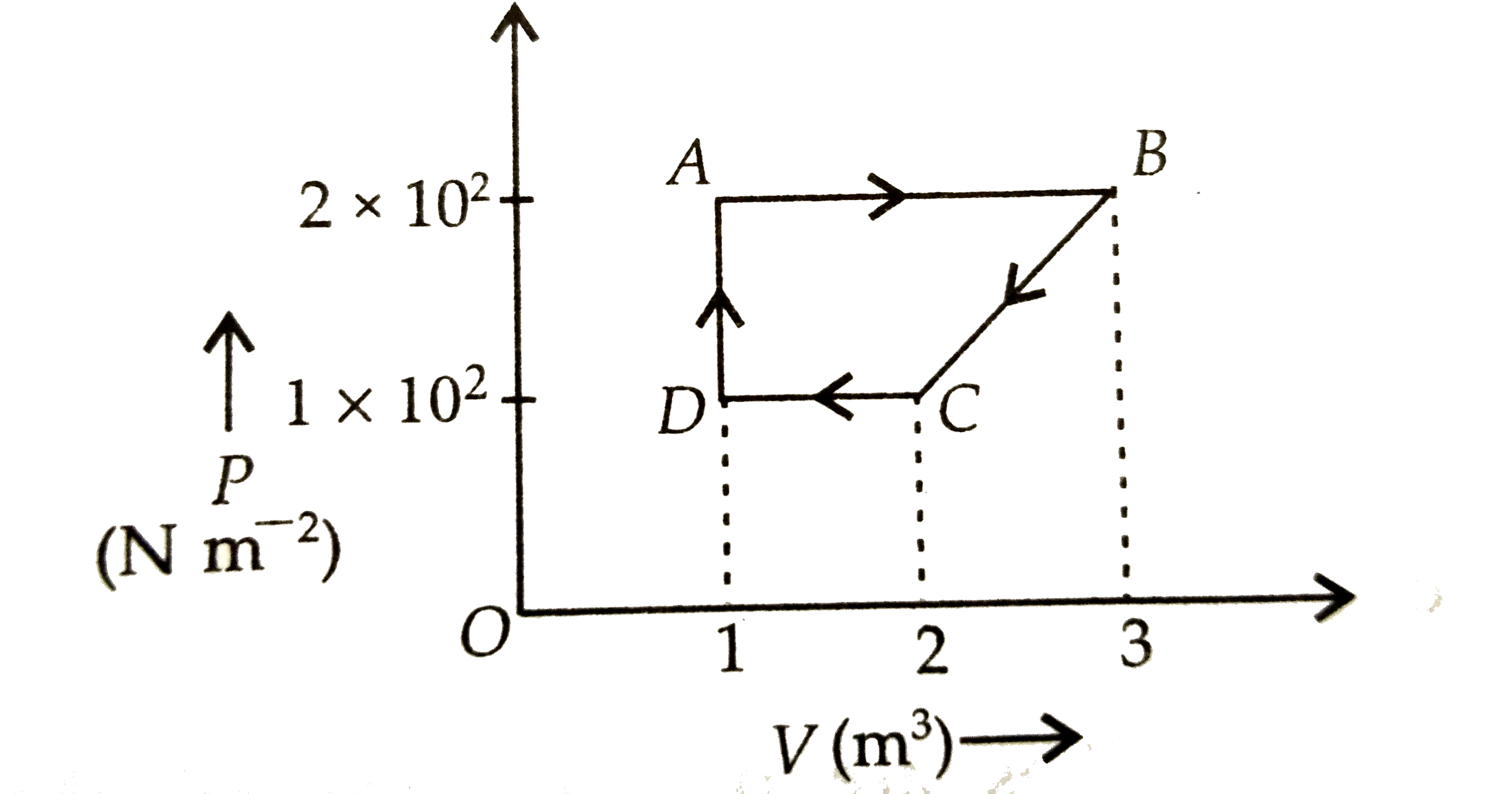 A1600 JB150 JC600 JD900 J
A1600 JB150 JC600 JD900 J
16kg oxygen gas expands at STP to occupy double of its oxygen volume. The work done during the process is:
View SolutionOne litre of an ideal gas at a pressure of 6 atm undergoes an adiabatic expansion until its pressure drops to one atmosphere and volume increases to 2 litre. Find the word done during the process. [γ=1.4].
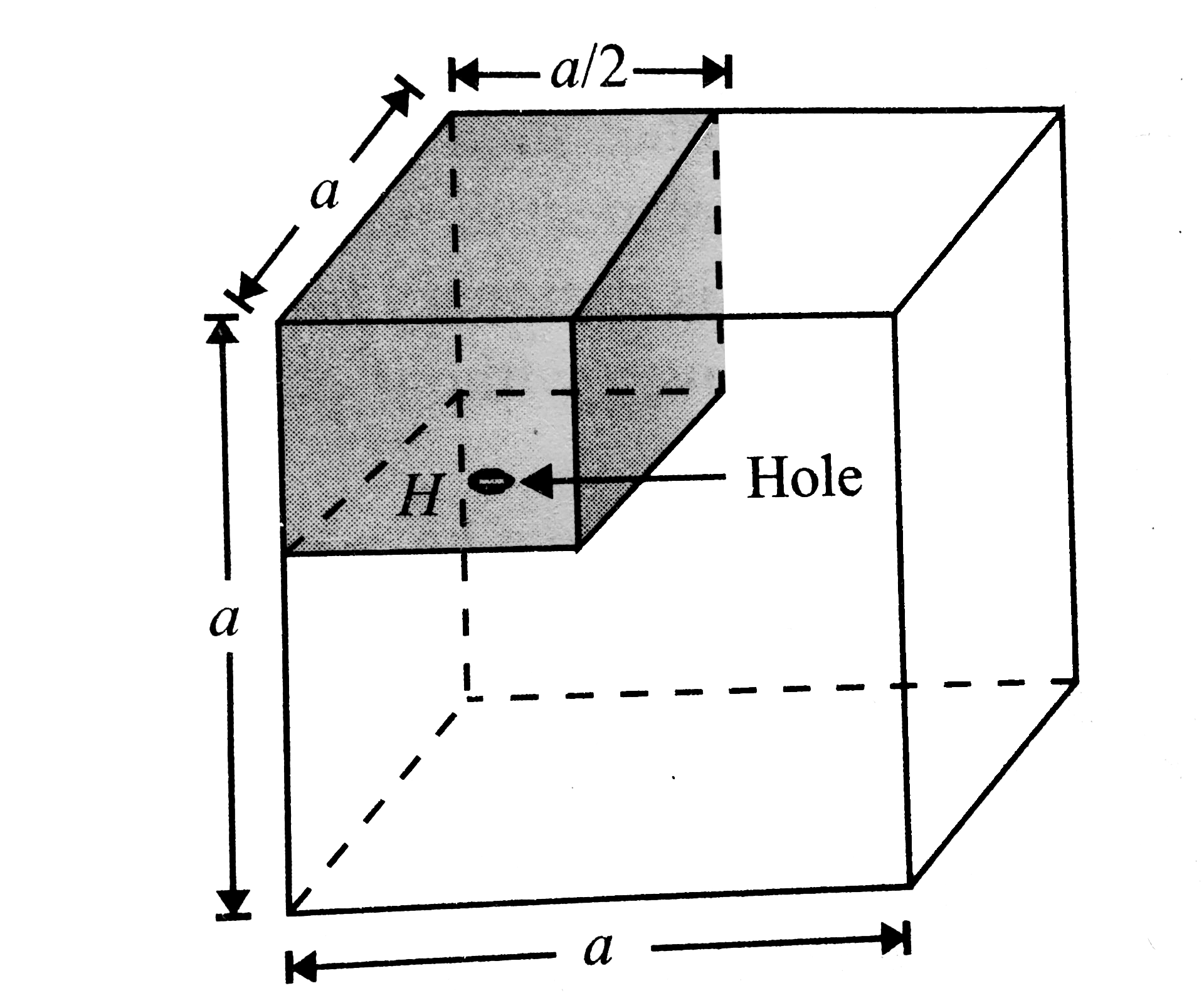
View SolutionFigure shows a hollow cube of side 'a' and volume 'V'. There is a small chamber of volume V/4 in the cube as shown. The chamber is completely filled by in kg of water. Water leaks through a hole H and spreads in the whole cube. Then the work done by gravity in this process assuming that the complete water finally lies at the bottom of the cube is
View SolutionThe change in internal energy of two moles of a gas during adiabatic expansion is found to be -100 Joule. The work done during the process is
View SolutionAn ideal gas goes from the state i to the state ∫ as shown in .the work done by the gas during the process

View Solution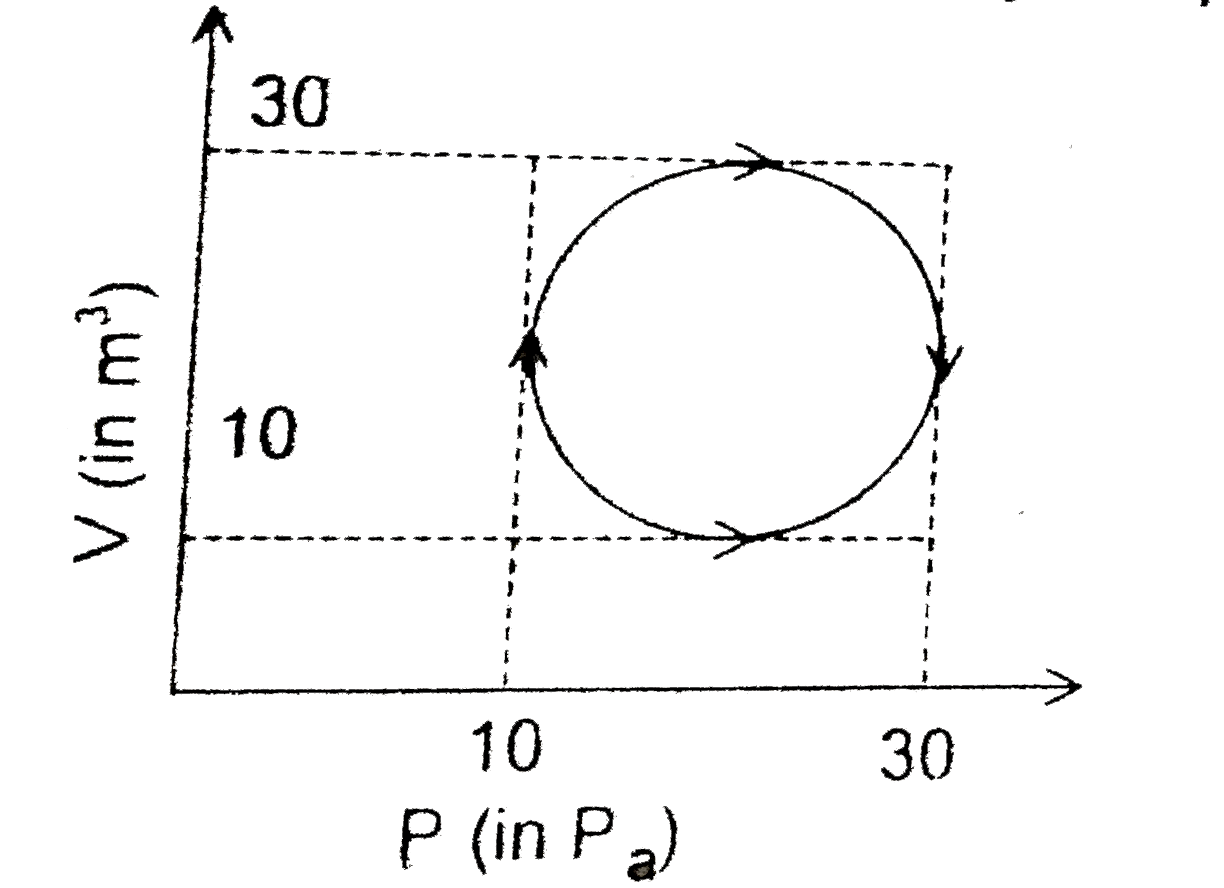
A system works under cyclic process as follow
Heat absorbed during the process is
View Solution
