Two non-interacting inductor L1 = 2 mH and L2 = 5 mH are connected in parallel then respective ratio of
Flux is 1:1
Current is 5 : 4
Energy is 25 : 4
Energy is 4 : 25
To solve the problem of finding the ratio of the magnetic flux in two non-interacting inductors connected in parallel, we can follow these steps:
Step 1: Understand the given values
We have two inductors:
- L1=2mH=2×10−3H
- L2=5mH=5×10−3H
Step 2: Recognize the properties of inductors in parallel
When inductors are connected in parallel, the voltage across each inductor is the same. Therefore, we can write:
V1=V2
Step 3: Write the voltage-current relationship for each inductor
The voltage across an inductor is given by:
V=Ldidt
For the two inductors, we have:
V1=L1di1dt
V2=L2di2dt
Since V1=V2, we can equate the two expressions:
L1di1dt=L2di2dt
Step 4: Rearranging the equation
Rearranging gives:
L1di1dt=L2di2dt
This can be rewritten as:
di1di2=L2L1
Step 5: Substitute the values of L1 and L2
Substituting the values:
di1di2=5mH2mH=52
Step 6: Find the ratio of currents
Thus, the ratio of the currents I1 and I2 is:
I1I2=52
Step 7: Calculate the magnetic flux
The magnetic flux Φ in an inductor is given by:
Φ=L⋅I
So, for the two inductors:
- Φ1=L1⋅I1=2×10−3⋅I1
- Φ2=L2⋅I2=5×10−3⋅I2
Step 8: Find the ratio of magnetic fluxes
Now, we can find the ratio of the magnetic fluxes:
Φ1Φ2=L1⋅I1L2⋅I2=2mH⋅I15mH⋅I2
Substituting I1=52I2:
Φ1Φ2=2⋅52I25⋅I2=55=1
Conclusion
Thus, the ratio of the magnetic fluxes in the two inductors is:
Φ1:Φ2=1:1
We have two inductors:
- L1=2mH=2×10−3H
- L2=5mH=5×10−3H
When inductors are connected in parallel, the voltage across each inductor is the same. Therefore, we can write:
V1=V2
The voltage across an inductor is given by:
V=Ldidt
For the two inductors, we have:
V1=L1di1dt
V2=L2di2dt
L1di1dt=L2di2dt
Rearranging gives:
L1di1dt=L2di2dt
This can be rewritten as:
di1di2=L2L1
Substituting the values:
di1di2=5mH2mH=52
Thus, the ratio of the currents I1 and I2 is:
I1I2=52
The magnetic flux Φ in an inductor is given by:
Φ=L⋅I
So, for the two inductors:
- Φ1=L1⋅I1=2×10−3⋅I1
- Φ2=L2⋅I2=5×10−3⋅I2
Now, we can find the ratio of the magnetic fluxes:
Φ1Φ2=L1⋅I1L2⋅I2=2mH⋅I15mH⋅I2
Φ1Φ2=2⋅52I25⋅I2=55=1
Thus, the ratio of the magnetic fluxes in the two inductors is:
Φ1:Φ2=1:1
Topper's Solved these Questions
Similar Questions
Two coils of self inductance L1 and L2 are connected in parallel and then connected to a cell of emf ε and internal resistance - R. Find the steady state current in the coils.
View SolutionTwo inductors L1 and L2 are connected in parallel and a time varying current flows as shown.
the ratio of current i1/i2
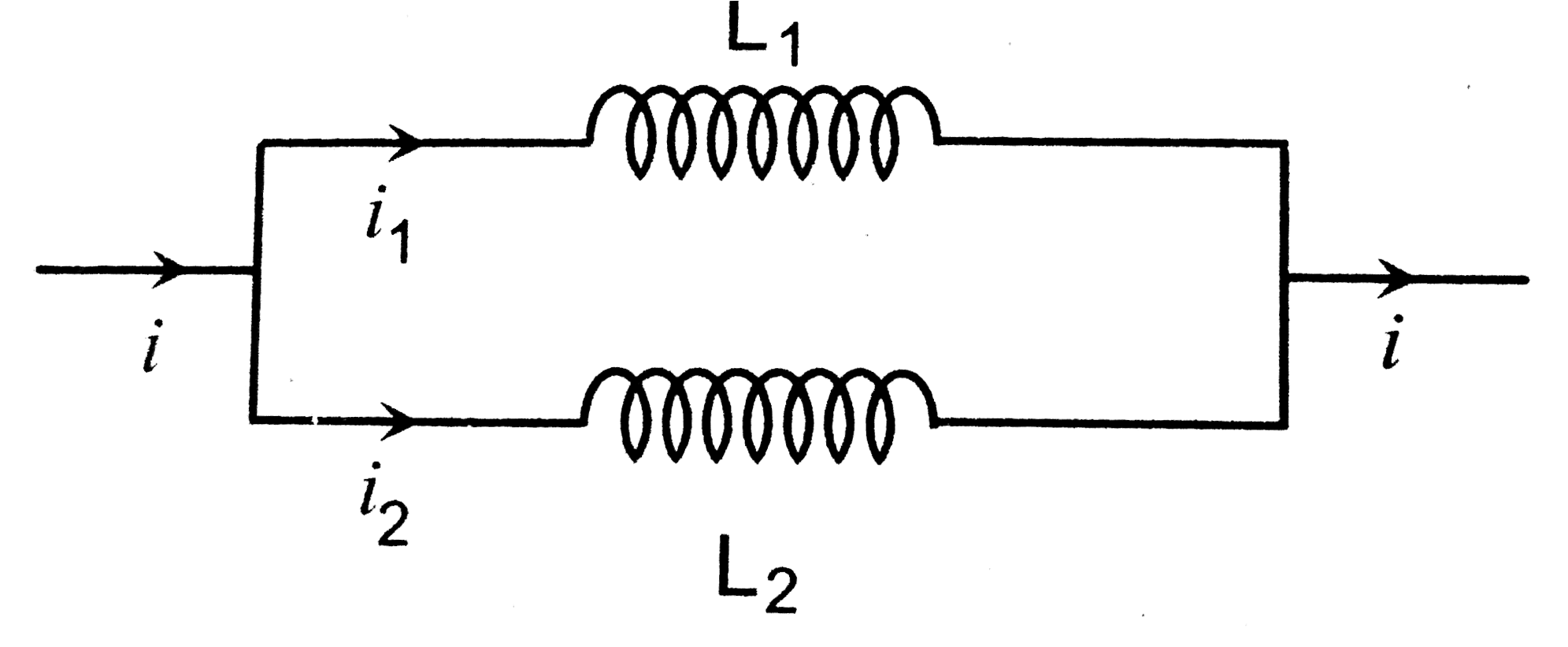
View Solution
Knowledge Check
Two inductors L1 and L2 are connected in parallel and a time varying current flows as shown.
The ratio of current i1/i2 is?
 AL2L1BL1L2CL22(L1+L2)2DL21(L1+L2)2
AL2L1BL1L2CL22(L1+L2)2DL21(L1+L2)2Two coils have self-inductance L1=4mH and L2=1mH respectively. The currents in the two coils are increased at the same rate. At a certain instant of time both coils are given the same power. If I1 and I2 are the currents in the two coils, at that instant of time respectively, then the value of (I1/I2) is :
A18B14C12D1
Show that if two inductors with equal inductance L are connected in parallel then the equivalent inductance of combination is L/2.The inductors are separated by a large distance.
View SolutionTwo pure inductors each of self-inductance L are connected in parallel but are well separted from each other. The total inductance is
View SolutionTwo inductors each of inductance L are connected in parallel. One more inductor of value 5 mH is connected in series of this configuration then the effective inductance is 15 mH . The value of L is ………..mH.
View SolutionIf resistance R =10Ω, inductance L = 2 mH and capacitance C=5μF are connected in series to an AC source of frequency 50 Hz, then at resonance the impedance of circuit is
View SolutionIf resistance R =100 Omega, inductance L = 12mH and capacitance C=15muF are connected in series to an AC sources, then at resonance the impedance of circuit is
View SolutionTwo ends of an inductor of inductance L are connected to two parallel conducting wires. A rod of length l and mass m is gien velocity v0 as shown. The whole sytem is placed in perpendicular magnetic field B. Find the maximum current in the inductor. (Neglect gravity and friction)

View Solution
