A square plate lies in the xy plane with its centre at the origin and its edges parallel to the x and y axes. Its moments of inertia about the x, y and z axes are Ix,Iy and IZ respectively, and about a diagonal it is ID
IX=IY=12IZ
IX=IY=2Ix
ID=Ix
ID=IY
The correct Answer is:A, C
To solve the problem, we need to find the relationships between the moments of inertia of a square plate about its axes and its diagonal. Here are the steps to derive the required relationships:
Step 1: Understand the Geometry
The square plate lies in the xy-plane with its center at the origin. The edges of the square are parallel to the x and y axes.
Step 2: Identify Moments of Inertia
For a square plate of uniform density:
- The moment of inertia about the x-axis, Ix
- The moment of inertia about the y-axis, Iy
- The moment of inertia about the z-axis, Iz
- The moment of inertia about a diagonal, Id
Step 3: Use the Perpendicular Axis Theorem
According to the perpendicular axis theorem, for a planar body lying in the xy-plane:
Iz=Ix+Iy
Since the plate is square and symmetrical, we have:
Ix=Iy
Let Ix=Iy=I. Therefore, we can rewrite the equation as:
Iz=I+I=2I
From this, we can express I in terms of Iz:
I=12Iz
Thus, we have:
Ix=Iy=12Iz
Step 4: Find the Moment of Inertia about the Diagonal
For a square plate, the moment of inertia about a diagonal can also be derived using the symmetry of the square. The moment of inertia about the diagonal Id can be expressed as:
Id=12Iz
This is because the diagonal divides the square into two equal halves, and the distribution of mass is symmetric about the diagonal.
Step 5: Relate Id to Ix
From the previous steps, we have:
Id=12Iz
And since we found that I=12Iz, we can conclude:
Id=Ix
Thus, we have:
Id=Ix=Iy
Final Relationships
From the above deductions, we can summarize the relationships:
1. Ix=Iy=12Iz
2. Id=Ix=Iy
Summary
- The moments of inertia about the x and y axes are equal and half of the moment of inertia about the z-axis.
- The moment of inertia about the diagonal is equal to the moments of inertia about the x and y axes.
The square plate lies in the xy-plane with its center at the origin. The edges of the square are parallel to the x and y axes.
For a square plate of uniform density:
- The moment of inertia about the x-axis, Ix
- The moment of inertia about the y-axis, Iy
- The moment of inertia about the z-axis, Iz
- The moment of inertia about a diagonal, Id
According to the perpendicular axis theorem, for a planar body lying in the xy-plane:
Iz=Ix+Iy
Since the plate is square and symmetrical, we have:
Ix=Iy
Let Ix=Iy=I. Therefore, we can rewrite the equation as:
Iz=I+I=2I
From this, we can express I in terms of Iz:
I=12Iz
Thus, we have:
Ix=Iy=12Iz
For a square plate, the moment of inertia about a diagonal can also be derived using the symmetry of the square. The moment of inertia about the diagonal Id can be expressed as:
Id=12Iz
This is because the diagonal divides the square into two equal halves, and the distribution of mass is symmetric about the diagonal.
From the previous steps, we have:
Id=12Iz
And since we found that I=12Iz, we can conclude:
Id=Ix
Thus, we have:
Id=Ix=Iy
From the above deductions, we can summarize the relationships:
1. Ix=Iy=12Iz
2. Id=Ix=Iy
- The moments of inertia about the x and y axes are equal and half of the moment of inertia about the z-axis.
- The moment of inertia about the diagonal is equal to the moments of inertia about the x and y axes.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 2 (Torque, Fixed and Rotation)10videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 2 (General rigid body motion, Rolling)10videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 1 (Mixed Numerical Questions)15videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS25videos
REVISION TEST-2 JEE
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question46videos
SIMPLE HARMONIC MOTION
Similar Questions
A uniform disc of radius R lies in x-y plane with its centre at origin. Its moment of inertia about the axis x=2R and y=0 is equal to the moment of inertia about the axis y=d and z=0, where d is equal to
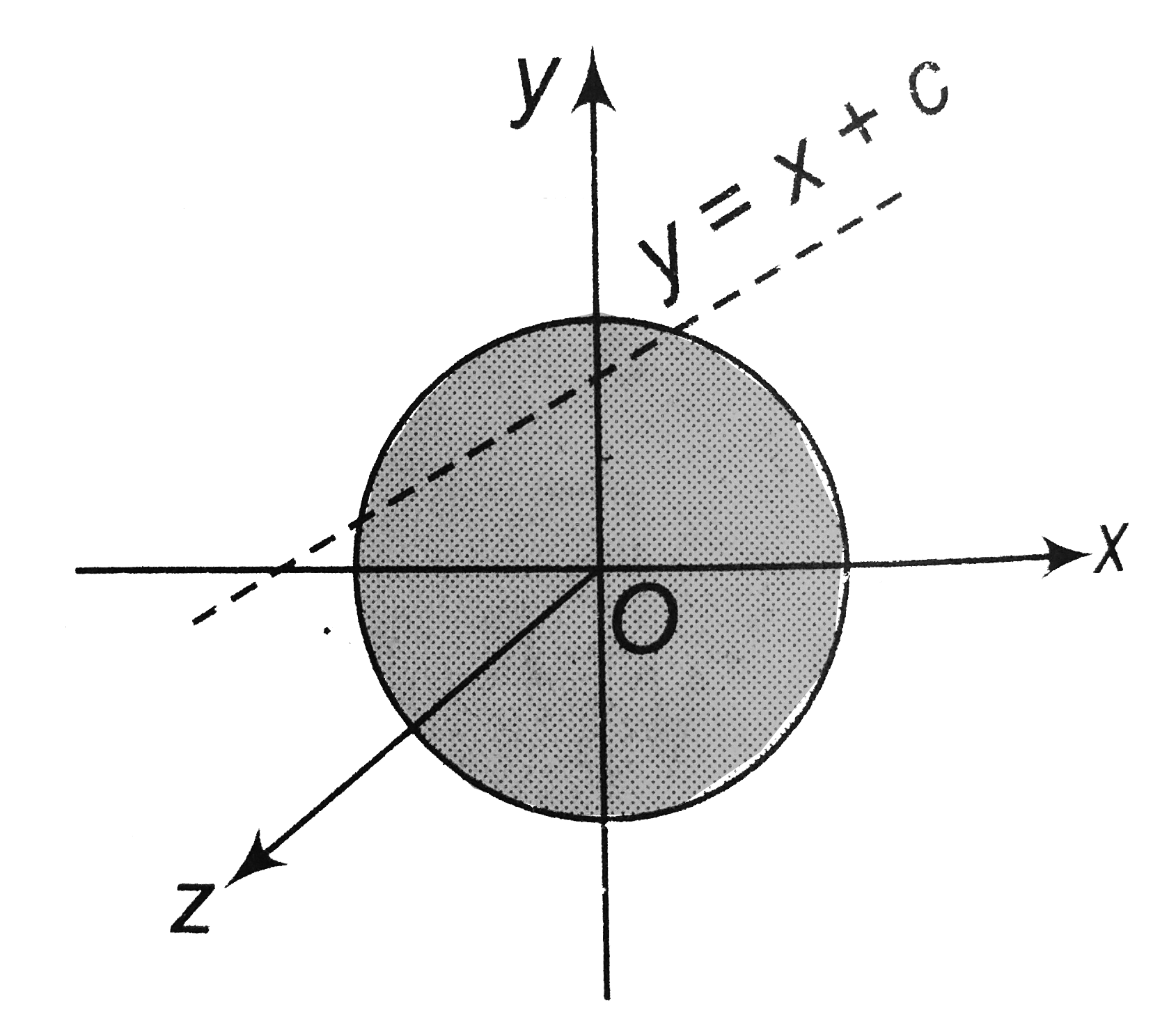
View SolutionA uniform disc of radius R lies in the x−y plane, with its centre at origin. Its moment of inertia about z-axis is equal to its moment of inertia about line y=x+c. The value of c will be.
 .View Solution
.View SolutionFour identical rods each of mass m and length l are joined to form a rigid square frame. The frame lies in the xy plane, with its centre at the origin and the sides parallel to the x and y axes. Its moment of inertia about
View SolutionA rod is placed along the line,y=2x with its centre at origin. The moment of inertia of the rod is maximum about.
View SolutionA thin circular disk is in the xy plane as shown in the figure. The ratio of its moment of inertia about z and z' axes will be :
View SolutionThe moment of inertia of a ring about its geometrical axis is I, then its moment of inertia about its diameter will be
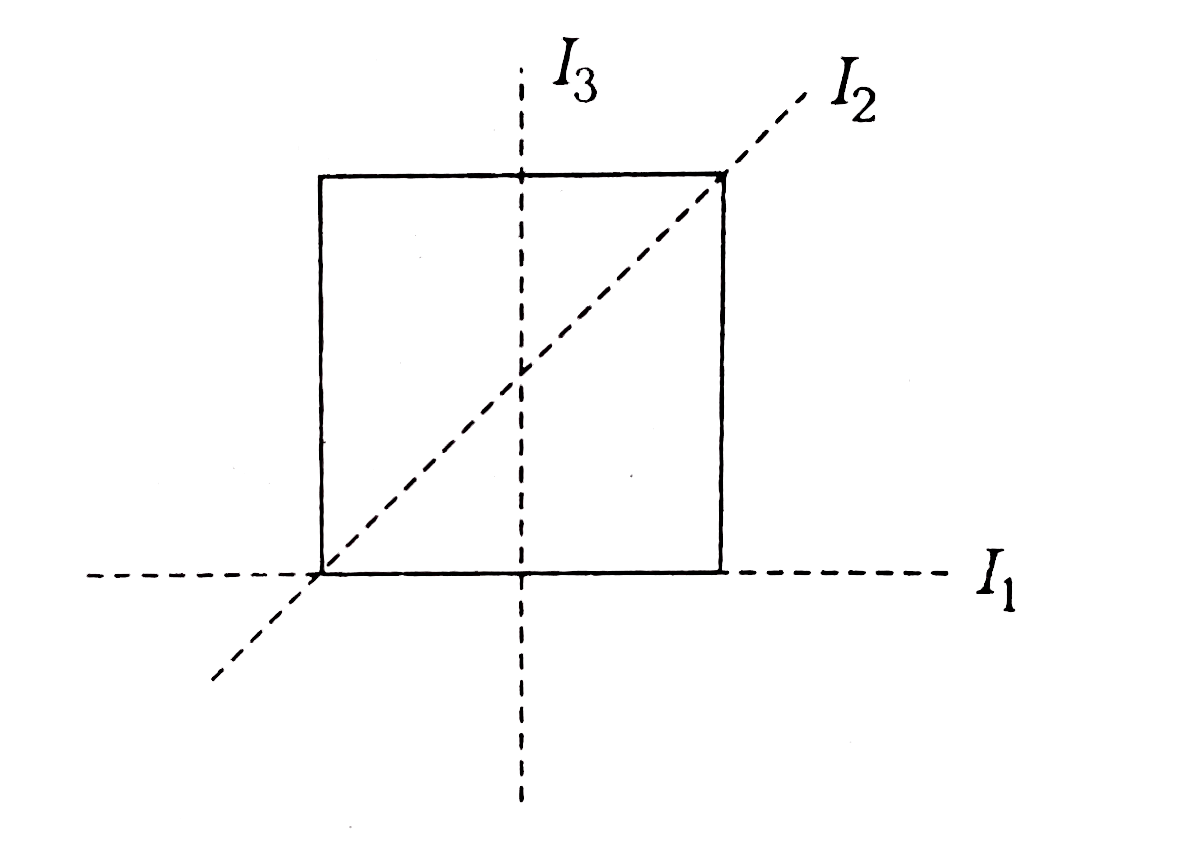
View SolutionA square lamina is as shown in figure. The moment of inertia of the frame about the three axes as shown in figure I1,I2andI3 respectively. Select the correct alternative.
 View Solution
View SolutionA point lies on the x-axis. Find its y and z-cordinates
View SolutionA point lies on the x-axis. Find its y and z-cordinates
View SolutionThe density of a rod AB increases linearly from A to B its midpoint is O and its centre of mass is at C. four axes pass through A, B, O and C, all perpendicular to the length of the rod. The moment of inertial of the rod about these axes are IA,IB,IO and IC respectively.
View Solution

