Moment of inertia of a disc about an axis which is tangent and parallel to its plane is I . Then the moment of inertia of disc about a tangent, but perpendicular to its plane will be
65I
34I
32I
54I
The correct Answer is:A
To find the moment of inertia of a disc about an axis that is tangent and perpendicular to its plane, we can follow these steps:
Step 1: Understand the given information
We know that the moment of inertia of the disc about an axis that is tangent and parallel to its plane is given as I. We need to find the moment of inertia about an axis that is tangent but perpendicular to its plane.
Step 2: Use the parallel axis theorem
The parallel axis theorem states that the moment of inertia about any axis parallel to an axis through the center of mass is given by:
I=Icm+Md2
where Icm is the moment of inertia about the center of mass, M is the mass of the object, and d is the distance between the two axes.
Step 3: Calculate the moment of inertia about the center of mass
For a disc, the moment of inertia about the center of mass (which is perpendicular to the plane of the disc) is:
Icm=12MR2
Step 4: Find the moment of inertia about the tangent and parallel axis
For the tangent and parallel axis, we have:
I=Icm+M(R)2
Substituting Icm:
I=12MR2+M(R)2=12MR2+MR2=32MR2
However, we know from the problem statement that this is equal to I.
Step 5: Relate I to MR2
From the previous step, we can express MR2 in terms of I:
I=32MR2⟹MR2=23I
Step 6: Find the moment of inertia about the tangent and perpendicular axis
Now, we need to find the moment of inertia about the tangent and perpendicular axis. Using the parallel axis theorem again:
Iperpendicular=Icm+M(R)2
Here, the distance d is R (the radius of the disc):
Iperpendicular=Icm+M(R)2=12MR2+M(R)2=12MR2+MR2=32MR2
Step 7: Substitute MR2 into the equation
Substituting MR2=23I into the equation:
Iperpendicular=32(23I)=I
Step 8: Final calculation
Now we can find the moment of inertia about the tangent and perpendicular axis:
Iperpendicular=32(23I)=32⋅23I=I
Conclusion
Thus, the moment of inertia of the disc about a tangent and perpendicular axis is:
Iperpendicular=65I
We know that the moment of inertia of the disc about an axis that is tangent and parallel to its plane is given as I. We need to find the moment of inertia about an axis that is tangent but perpendicular to its plane.
The parallel axis theorem states that the moment of inertia about any axis parallel to an axis through the center of mass is given by:
I=Icm+Md2
where Icm is the moment of inertia about the center of mass, M is the mass of the object, and d is the distance between the two axes.
For a disc, the moment of inertia about the center of mass (which is perpendicular to the plane of the disc) is:
Icm=12MR2
For the tangent and parallel axis, we have:
I=Icm+M(R)2
Substituting Icm:
I=12MR2+M(R)2=12MR2+MR2=32MR2
However, we know from the problem statement that this is equal to I.
From the previous step, we can express MR2 in terms of I:
I=32MR2⟹MR2=23I
Now, we need to find the moment of inertia about the tangent and perpendicular axis. Using the parallel axis theorem again:
Iperpendicular=Icm+M(R)2
Here, the distance d is R (the radius of the disc):
Iperpendicular=Icm+M(R)2=12MR2+M(R)2=12MR2+MR2=32MR2
Substituting MR2=23I into the equation:
Iperpendicular=32(23I)=I
Now we can find the moment of inertia about the tangent and perpendicular axis:
Iperpendicular=32(23I)=32⋅23I=I
Thus, the moment of inertia of the disc about a tangent and perpendicular axis is:
Iperpendicular=65I
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 2 (Torque, Fixed and Rotation)10videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 2 (General rigid body motion, Rolling)10videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 1 (Mixed Numerical Questions)15videos
ROTATIONAL MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS25videos
REVISION TEST-2 JEE
- BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question46videos
SIMPLE HARMONIC MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
If the moment of inertion of a disc about an axis tangentially and parallel to its surface by I, then what will be the moment of inertia about the axis tangential but perpendicular to the surface
A65IB34IC32ID54I
Calculate the moment of inertia of a disc about its any diameter ?
View SolutionCalculate the moment of inertia of a disc about its any diameter ?
View SolutionA symmetric lamina of mass M consists of a square shape with a semicircular section over each of the edge of the square as in fig. The side of the square is 2a.
The moment of inertia of the lamina about an axis through its centre of mass and perpendicular to the plane is 1.6Ma2. The moment of inertia of the lamina about the tangent AB in the plane of lamina is.
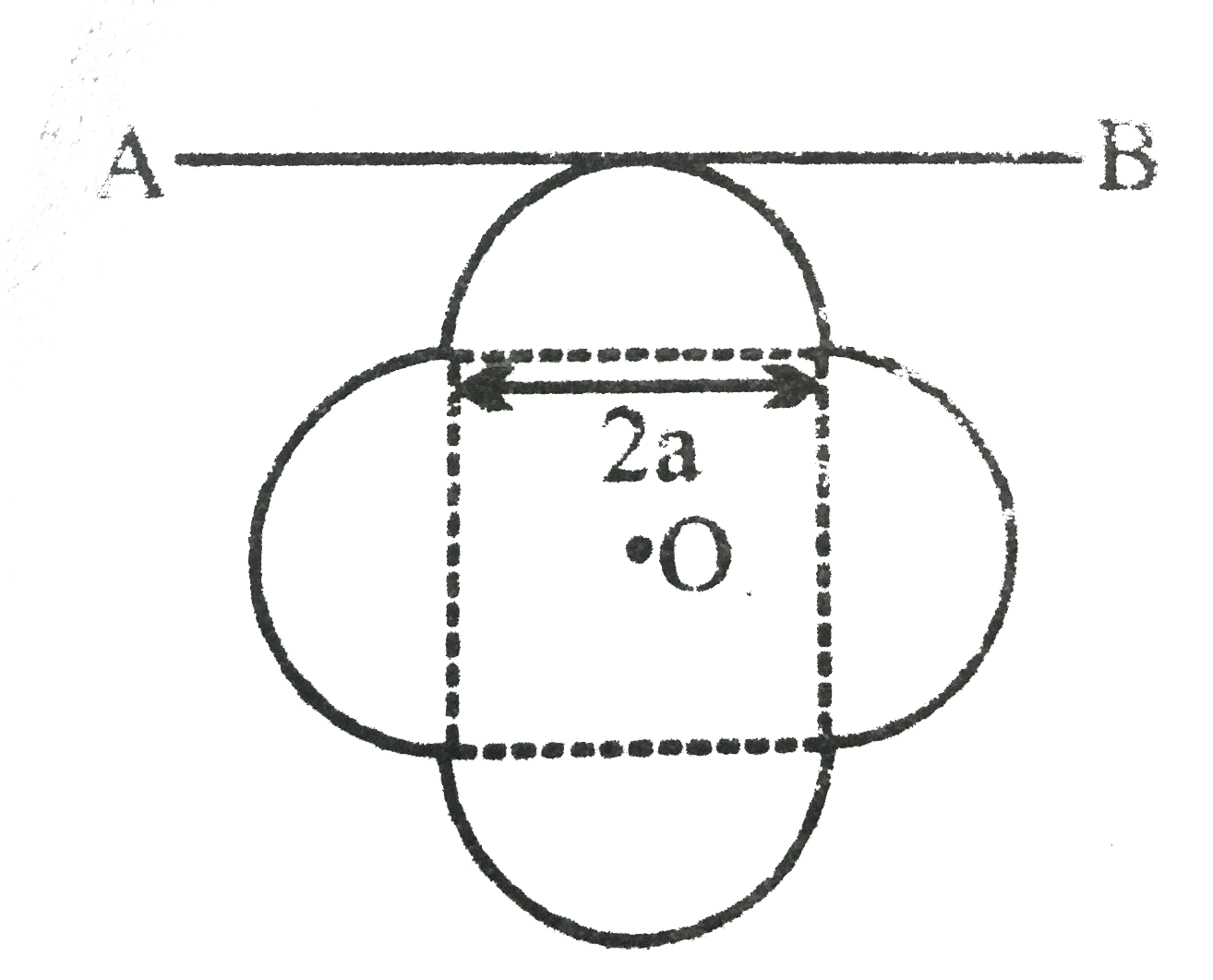 .View Solution
.View SolutionThe moment of inertia of a disc of mass M and radius R about a tangent to its rim in its plane is
View SolutionThe moment of inertia of a uniform ring about an axis passing through its centre and perpendicular to its plane is 100kgm2. What is the moment of inertia of the ring about its diameter ?
View SolutionThe moment of inertia of a uniform ring about an axis passing through its centre and perpendicular to its plane is 100kgm2. What is the moment of inertia of the ring about its diameter ?
View SolutionThe moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is I0. What is the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod ?
View Solution

