A force Fˆk acts on O, the origin of the coordinate system. The torque of this force about the point is: (1,−1) is
F(ˆi+ˆj)
−F(ˆi−ˆj)
F(−ˆi−ˆj)
−F(ˆi+ˆj)
The correct Answer is:A
To find the torque of the force ^F^k acting at the origin about the point (1,−1), we can follow these steps:
Step 1: Identify the Force and the Points
The force is given as ^F^k, which means it acts in the z-direction. The point about which we want to calculate the torque is A(1,−1).
Step 2: Define the Position Vectors
- The position vector of the origin O is →rO=(0,0,0).
- The position vector of point A is →rA=(1,−1,0).
Step 3: Calculate the Position Vector →R from Point A to the Origin
The position vector →R from point A to the origin O is given by:
→R=→rO−→rA=(0,0,0)−(1,−1,0)=(−1,1,0)
Step 4: Write the Force Vector
The force vector is:
→F=(0,0,F)
Step 5: Calculate the Torque →τ
The torque →τ is calculated using the cross product:
→τ=→R×→F
Substituting the vectors:
→τ=(−1,1,0)×(0,0,F)
Step 6: Compute the Cross Product
Using the determinant form for the cross product:
→τ=∣∣
∣
∣∣^i^j^k−11000F∣∣
∣
∣∣
Calculating this determinant:
→τ=^i(1⋅F−0⋅0)−^j(−1⋅F−0⋅0)+^k(−1⋅0−1⋅0)
This simplifies to:
→τ=^iF+^jF=F^i+F^j
Final Result
Thus, the torque about the point (1,−1) is:
→τ=F(^i+^j)
---
The force is given as ^F^k, which means it acts in the z-direction. The point about which we want to calculate the torque is A(1,−1).
- The position vector of the origin O is →rO=(0,0,0).
- The position vector of point A is →rA=(1,−1,0).
The position vector →R from point A to the origin O is given by:
→R=→rO−→rA=(0,0,0)−(1,−1,0)=(−1,1,0)
The force vector is:
→F=(0,0,F)
The torque →τ is calculated using the cross product:
→τ=→R×→F
Substituting the vectors:
→τ=(−1,1,0)×(0,0,F)
Using the determinant form for the cross product:
→τ=∣∣
∣
∣∣^i^j^k−11000F∣∣
∣
∣∣
Calculating this determinant:
→τ=^i(1⋅F−0⋅0)−^j(−1⋅F−0⋅0)+^k(−1⋅0−1⋅0)
This simplifies to:
→τ=^iF+^jF=F^i+F^j
Thus, the torque about the point (1,−1) is:
→τ=F(^i+^j)
Topper's Solved these Questions
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (SINGLE OPTION CORRECT TYPE)
Explore 26 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:JEE Advanced (Archive) (MULTIPLE OPTIONS CORRECT TYPE)
Explore 17 Videos
- ROTATIONAL MOTION Book:VMC MODULES ENGLISHChapter:ROTATIONAL MOTION Exercise:LEVEL - 2 (Angular Momentum, Collision)
Explore 20 Videos
- REVISION TEST-2 JEEBook:VMC MODULES ENGLISHChapter:REVISION TEST-2 JEEExercise:PHYSICS
Explore 25 Videos
- SIMPLE HARMONIC MOTION Book:VMC MODULES ENGLISHChapter:SIMPLE HARMONIC MOTION Exercise:7-previous year question
Explore 46 Videos
Similar Questions
A force of −4Fˆk acts at O, the origin of the coordinate system. The torque about the point (1,−1) is
View SolutionStatement-I : Magnitude of torque of a force about a given point does not depend upon the location of the origin of the co-ordinate system.
Statement II: Moment of couple is different for different points in its plane
View Solution
Knowledge Check
Let →F be a force acting on a particle having positon vector →r.Let→τ be the torque of this force about the origin then
A→r.→τ>0 and →F.→τ<0B→r.→τ=0 and →F.→τ=0C→r.→τ=0 and →F.→τ≠0D→r.→τ≠0 and →F.→τ=0
Let a force F be acting on a body free to rotate about a point O and let r the position vector of ant point P on the line of aciton of the force. Then torque (τ) of this force abot point O is defined as τ=r×F Given, F=(2ˆi+3ˆj−ˆk)Nandr=(ˆi−ˆj+6ˆk)m Find the torque of this force.
View SolutionLet →F be the force acting on a particle having position vector →rand→T be the torque of this force about the origin. Then
View SolutionLet a force F be acting on a body free to rotate about a point O and let r the position vector of any point P on the line of action of the force. Then torque (τ) of this force about point O is defined as τ=r×F Given, F=(2ˆi+3ˆj−ˆk)Nandr=(ˆi−ˆj+6ˆk)m Find the torque of this force.
View SolutionThe moment of the force F acting at a point P, about the point C is
View SolutionA particle is placed at the origin of the coordinate system. Two forces of magnitude 20N&10N act on it as shown in figure. It is found that it starts moving towards the point (1,1) . The net unknown force acting on the particle at this position can be :
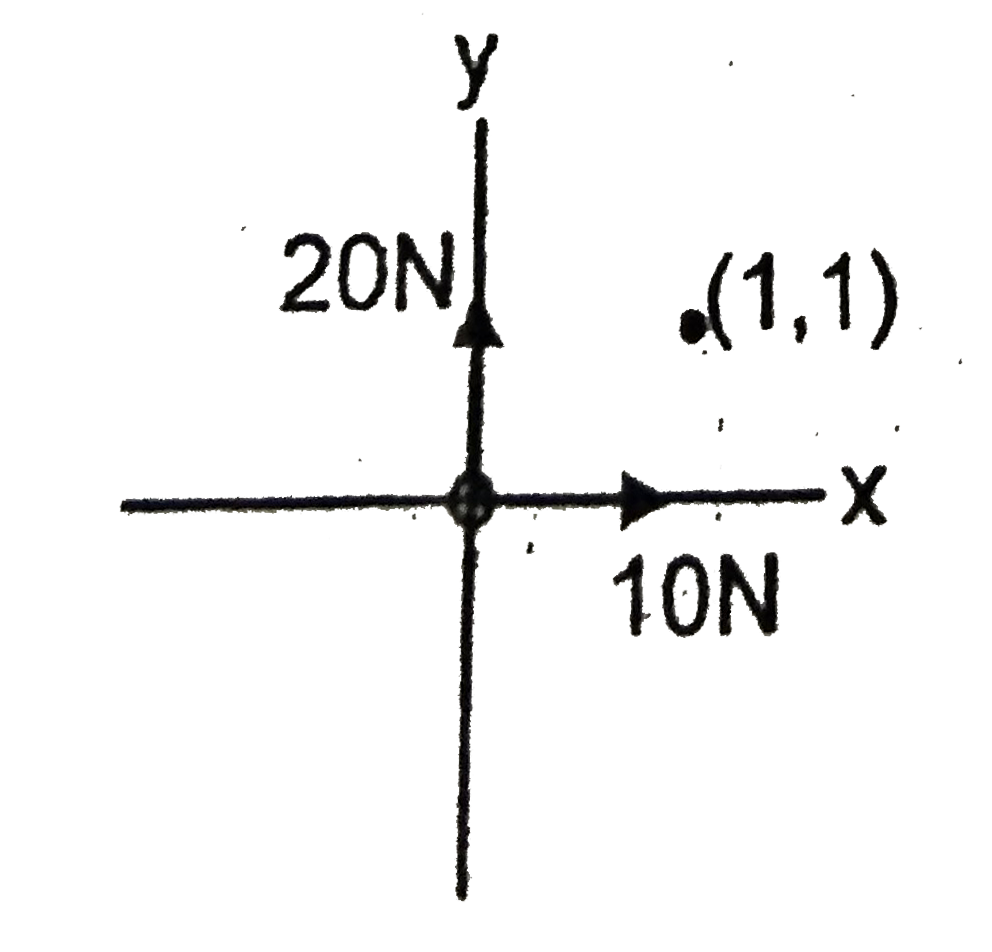
View SolutionA force (ˆi−2ˆj+3ˆk) acts on a particle lying at origin. What is the torque acting on the particle about the origin.
View SolutionA force F=(2ˆi+3ˆj−2ˆk)N is acting on a body at point (2m, 4m,−2m). Find torque of this force about origin.
View Solution