The moment of the force F acting at a point P, about the point C is
F×CP
CP⋅F
a vector having the same direction as F
CP×F
The correct Answer is:D
To solve the problem of finding the moment of a force F acting at a point P about the point C, we can follow these steps:
1. Understand the Concept of Moment of a Force:
The moment of a force about a point is defined as the cross product of the position vector (from the point to the line of action of the force) and the force vector itself. Mathematically, it is given by:
M=r×F
where M is the moment, r is the position vector, and F is the force vector.
2. Identify the Position Vector:
In this case, we need to find the position vector r from point C to point P. This can be expressed as:
r=P−C
or equivalently,
r=CP
3. Substitute the Position Vector into the Moment Equation:
Now, we can substitute r into the moment equation:
M=(P−C)×F
4. Final Expression for the Moment:
The moment of the force F acting at point P about point C is then given by:
M=CP×F
5. Conclusion:
Therefore, the moment of the force F acting at point P about point C is represented by the expression CP×F.
The moment of a force about a point is defined as the cross product of the position vector (from the point to the line of action of the force) and the force vector itself. Mathematically, it is given by:
M=r×F
where M is the moment, r is the position vector, and F is the force vector.
In this case, we need to find the position vector r from point C to point P. This can be expressed as:
r=P−C
or equivalently,
r=CP
Now, we can substitute r into the moment equation:
M=(P−C)×F
The moment of the force F acting at point P about point C is then given by:
M=CP×F
Therefore, the moment of the force F acting at point P about point C is represented by the expression CP×F.
Topper's Solved these Questions
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (More Than One Correct Option Type Questions)
35 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise (Statement I And Ii Type Questions)
12 Videos
- PRODUCT OF VECTORSBOOK - ARIHANT MATHS ENGLISHCHAPTER - PRODUCT OF VECTORSEXERCISE - Exercise For Session 4
10 Videos
- PROBABILITYBOOK - ARIHANT MATHS ENGLISHCHAPTER - PROBABILITYEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
54 Videos
- PROPERTIES AND SOLUTION OF TRIANGLES BOOK - ARIHANT MATHS ENGLISHCHAPTER - PROPERTIES AND SOLUTION OF TRIANGLES EXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
21 Videos
Similar Questions
Knowledge Check
There are four force acting at a point p produced by strings as shown in figure, which is at rest. The force F1 and F2 are .
 A1√2N,3√2NB3√2N,1√2NC1√2N,1√2ND3√2N,3√2N,
A1√2N,3√2NB3√2N,1√2NC1√2N,1√2ND3√2N,3√2N,
Forces 2ˆi+ˆj,2ˆi−3ˆj+6ˆkand−ˆi+2ˆj−ˆk act at a point P, with position vector 4ˆi−3ˆj−ˆk. Find the vector moment of the resultant of these forces about thepoint Q whose position vector is 6ˆi+ˆj=3ˆk
View SolutionA force of 39 kg. wt is acting at a point p ( -4,2,5) in the direaction 12ˆi−4ˆj−3ˆk . The moment of this force about a line through the origin having the direction of 2ˆi−2ˆj+ˆk is
View SolutionThe greatest and least resulant of two forces acting at a point is 10N and 6N,respectively. If each force is increased by 3N, find the resulant of new forces when acting at a point at an angle of 90∘ with each other .
View SolutionThe moment of the force, →F=4ˆi+5ˆj−6ˆk at (2,0,−3). About the point (2,−2,−2) is given by
View SolutionThere are four forces ,acting at a point P produced by strings as shown in figure. which is at rest. The forces F1andF2 are
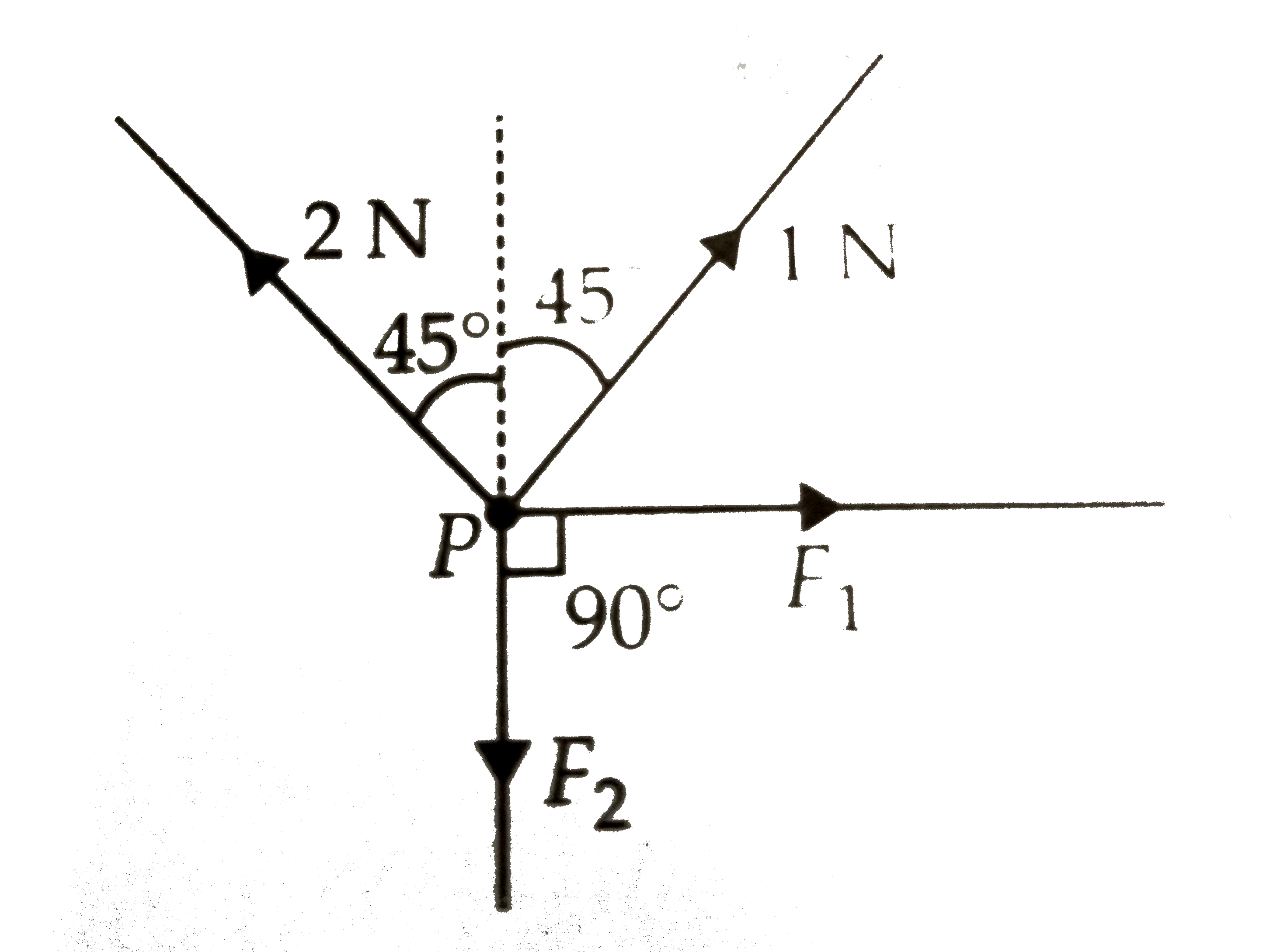
View SolutionThe moment of a force of 50 N about a point is 5 Nm. Find the perpendicular distance of force from that point.
View SolutionThe moment of a force of 10N about a fixed point O is 5 Nm. Calculate the distance of the point O from the line of action of the force.
View Solution
