A force of −4Fˆk acts at O, the origin of the coordinate system. The torque about the point (1,−1) is
−4F(ˆi−ˆj)
4F(ˆi−ˆj)
−4F(ˆi+ˆj)
4F(ˆi+ˆj)
To find the torque about the point (1, -1) due to a force of −4F^k acting at the origin, we can follow these steps:
Step 1: Define the position vector
The torque T is given by the cross product of the position vector r and the force vector F. The position vector r is defined as the vector from the point about which we are calculating the torque to the point of application of the force.
Given:
- The point about which we are calculating torque is P(1,−1).
- The point of application of the force is the origin O(0,0).
Thus, the position vector r from point P to point O is:
r=O−P=(0−1)^i+(0−(−1))^j=−^i+^j
Step 2: Write the force vector
The force vector is given as:
F=−4F^k
Step 3: Calculate the torque
The torque T is calculated using the cross product:
T=r×F
Substituting the values we have:
T=(−^i+^j)×(−4F^k)
Step 4: Set up the determinant for the cross product
We can express the cross product in terms of a determinant:
T=∣∣
∣
∣∣^i^j^k−11000−4F∣∣
∣
∣∣
Step 5: Calculate the determinant
Calculating the determinant, we have:
T=^i∣∣∣100−4F∣∣∣−^j∣∣∣−100−4F∣∣∣+^k∣∣∣−1100∣∣∣
Calculating each of the 2x2 determinants:
1. ∣∣∣100−4F∣∣∣=1⋅(−4F)−0⋅0=−4F
2. ∣∣∣−100−4F∣∣∣=−1⋅(−4F)−0⋅0=4F
3. ∣∣∣−1100∣∣∣=−1⋅0−1⋅0=0
Putting it all together:
T=−4F^i−4F^j+0^k=−4F^i−4F^j
Step 6: Final expression
Thus, we can write the torque as:
T=−4F^i+4F^j
Conclusion
The correct answer is option 3: −4F^i+^j.
The torque T is given by the cross product of the position vector r and the force vector F. The position vector r is defined as the vector from the point about which we are calculating the torque to the point of application of the force.
- The point about which we are calculating torque is P(1,−1).
- The point of application of the force is the origin O(0,0).
r=O−P=(0−1)^i+(0−(−1))^j=−^i+^j
The force vector is given as:
F=−4F^k
The torque T is calculated using the cross product:
T=r×F
Substituting the values we have:
T=(−^i+^j)×(−4F^k)
We can express the cross product in terms of a determinant:
T=∣∣
∣
∣∣^i^j^k−11000−4F∣∣
∣
∣∣
Calculating the determinant, we have:
T=^i∣∣∣100−4F∣∣∣−^j∣∣∣−100−4F∣∣∣+^k∣∣∣−1100∣∣∣
Calculating each of the 2x2 determinants:
1. ∣∣∣100−4F∣∣∣=1⋅(−4F)−0⋅0=−4F
2. ∣∣∣−100−4F∣∣∣=−1⋅(−4F)−0⋅0=4F
3. ∣∣∣−1100∣∣∣=−1⋅0−1⋅0=0
T=−4F^i−4F^j+0^k=−4F^i−4F^j
Thus, we can write the torque as:
T=−4F^i+4F^j
The correct answer is option 3: −4F^i+^j.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.120videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - Check point 9.220videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.14videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions2videos
ROTATIONAL MECHANICS
Similar Questions
A force Fˆk acts on O, the origin of the coordinate system. The torque of this force about the point is: (1,−1) is
View SolutionA particle is placed at the origin of the coordinate system. Two forces of magnitude 20N&10N act on it as shown in figure. It is found that it starts moving towards the point (1,1) . The net unknown force acting on the particle at this position can be :
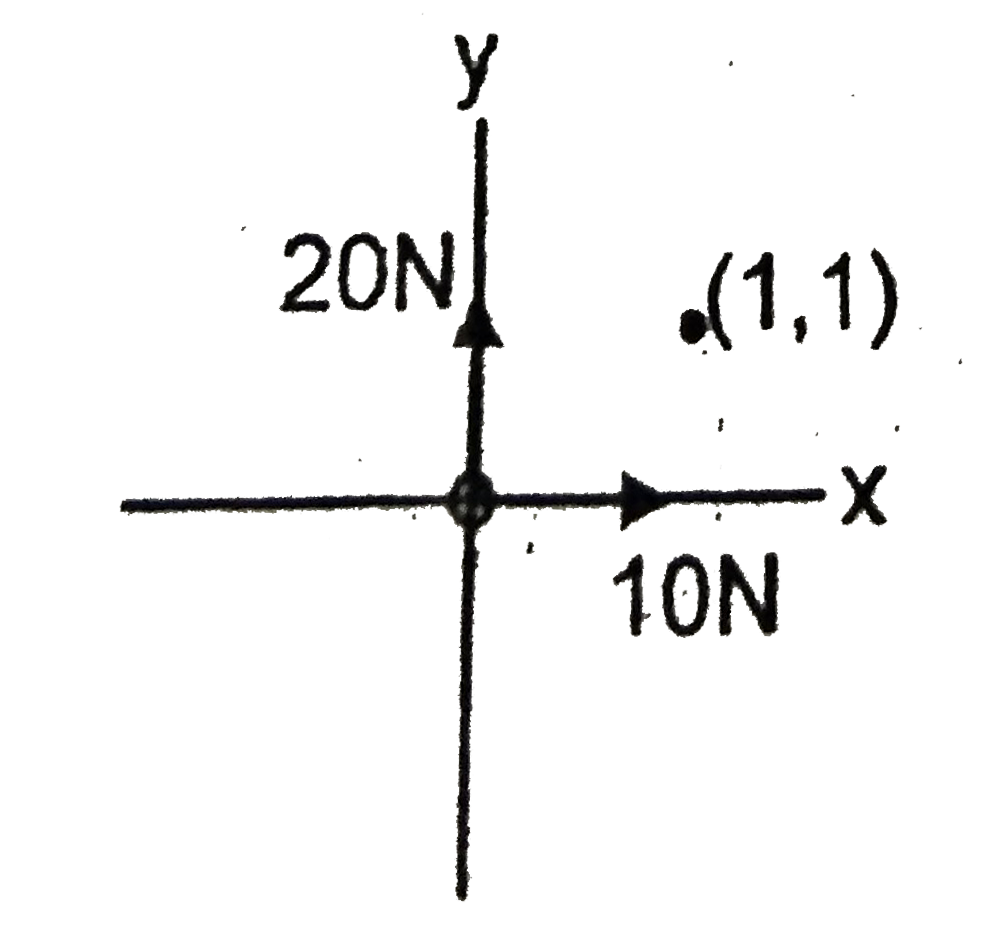 View Solution
View SolutionFollowing forces start acting on a particle at rest at the origin of the co-ordinate system
→F1=−4ˆI−5ˆj+5ˆk,→F2=5ˆI+8ˆj+6ˆk,→F3=−3ˆI+4ˆj−7ˆk and →F4=2ˆi−3ˆj−2ˆk then the particle will moveView SolutionFollowing forces start acting on a particle at rest at the origin of the co-ordinate system simultaneously →F1=−4ˆi+5ˆj+5ˆk,→F2=−5ˆi+8ˆj+6ˆk,→F3=−3ˆi+4ˆj−7ˆk and →F4=12ˆi−3ˆj−2ˆk then the particle will move-
View SolutionThe moment of the force F acting at a point P, about the point C is
View SolutionStatement-I : Magnitude of torque of a force about a given point does not depend upon the location of the origin of the co-ordinate system.
Statement II: Moment of couple is different for different points in its planeView SolutionFind the charge on the capacitor shown in figure
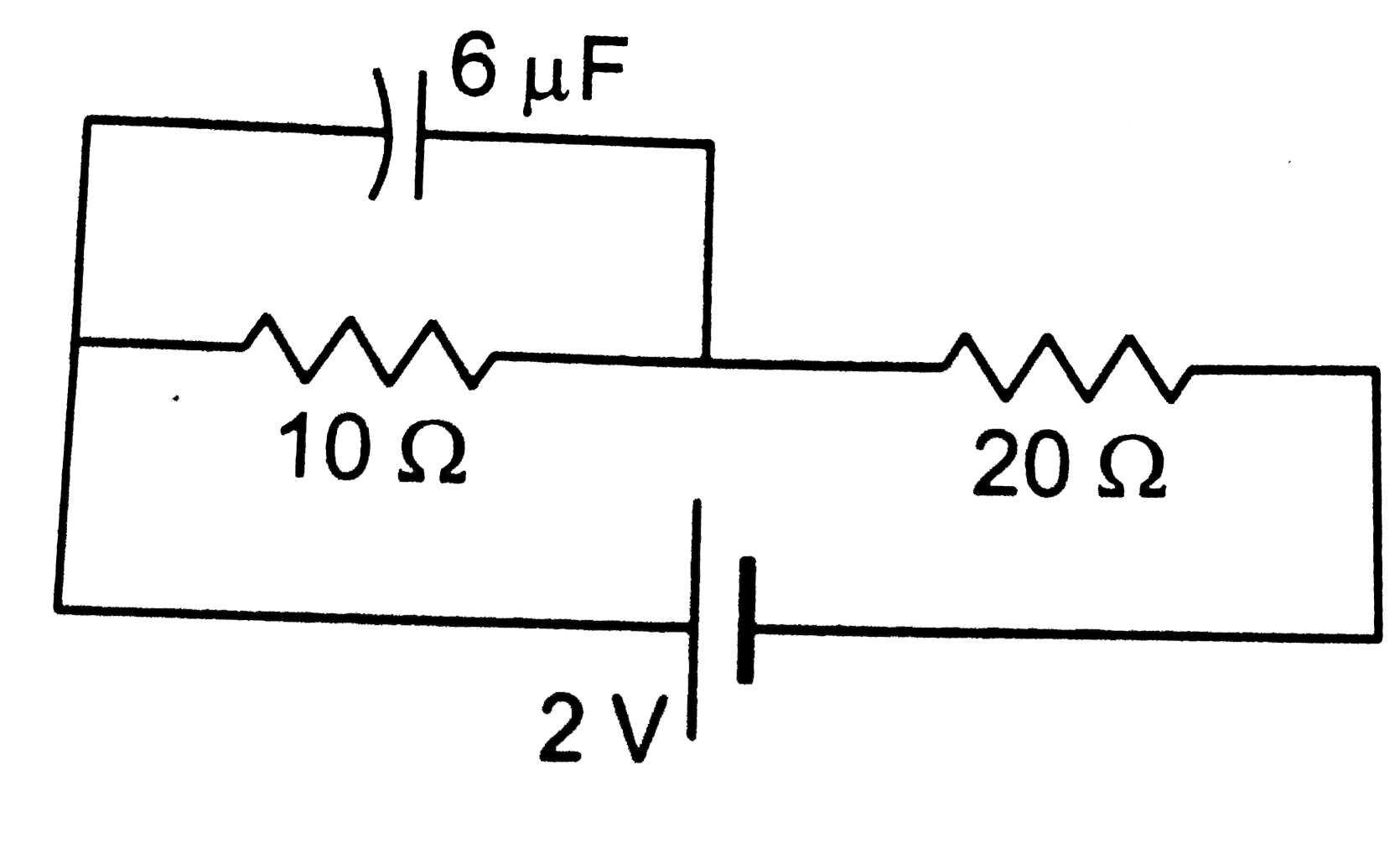 View Solution
View SolutionA force →F=4ˆi−10ˆj acts on a body at a point having position vector −5ˆi−3ˆj relative to origin of co-ordinates on the axis of rotation. The torque acting on the body is
View SolutionA force F=2ˆi+3ˆj−ˆk acts at a point (2,-3,1). Then magnitude of torque about point (0,0,2) will be
View SolutionA single force acts on a particle situated on the negative x-axis. The torque about the origin is in the positive z-direction. The force is
View Solution

