A circular disc of radius b has a hole of radius a at its centre (see figure) if the mass per unit area of the disc varies as $(\frac{σ_{0}}{r})$ then the radius of gyration of the disc about its axis passing through the centre is

A

$\frac{a + b}{2}$

B

$\sqrt{\frac{a^{2} + b^{2} + a b}{2}}$

C

$\sqrt{\frac{a^{2} + b^{2} + a b}{3}}$

D

$\frac{a + b}{3}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$I = \int d m r^{2} \Rightarrow \int_{a}^{b} (\frac{σ_{0}}{r} 2 π r d r) r^{2} \Rightarrow I = 2 σ_{0} π \frac{b^{2} - a^{2}}{3}$

$\to I = m k^{2} \Rightarrow 2 σ_{0} π \frac{b^{3} - a^{3}}{3} = 2 σ_{0} π (b - a) K^{2}$
$\Rightarrow k = \sqrt{\frac{a^{2} + b^{2} + c^{2}}{3}}$

Updated on:21/07/2023

|

Class 12 PHYSICS ROTATIONAL MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

From a uniform circular disc of radius R and mass 9M, a small disc of radius $\frac{R}{3}$ is removed as shown in the figure. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through centre of disc is :

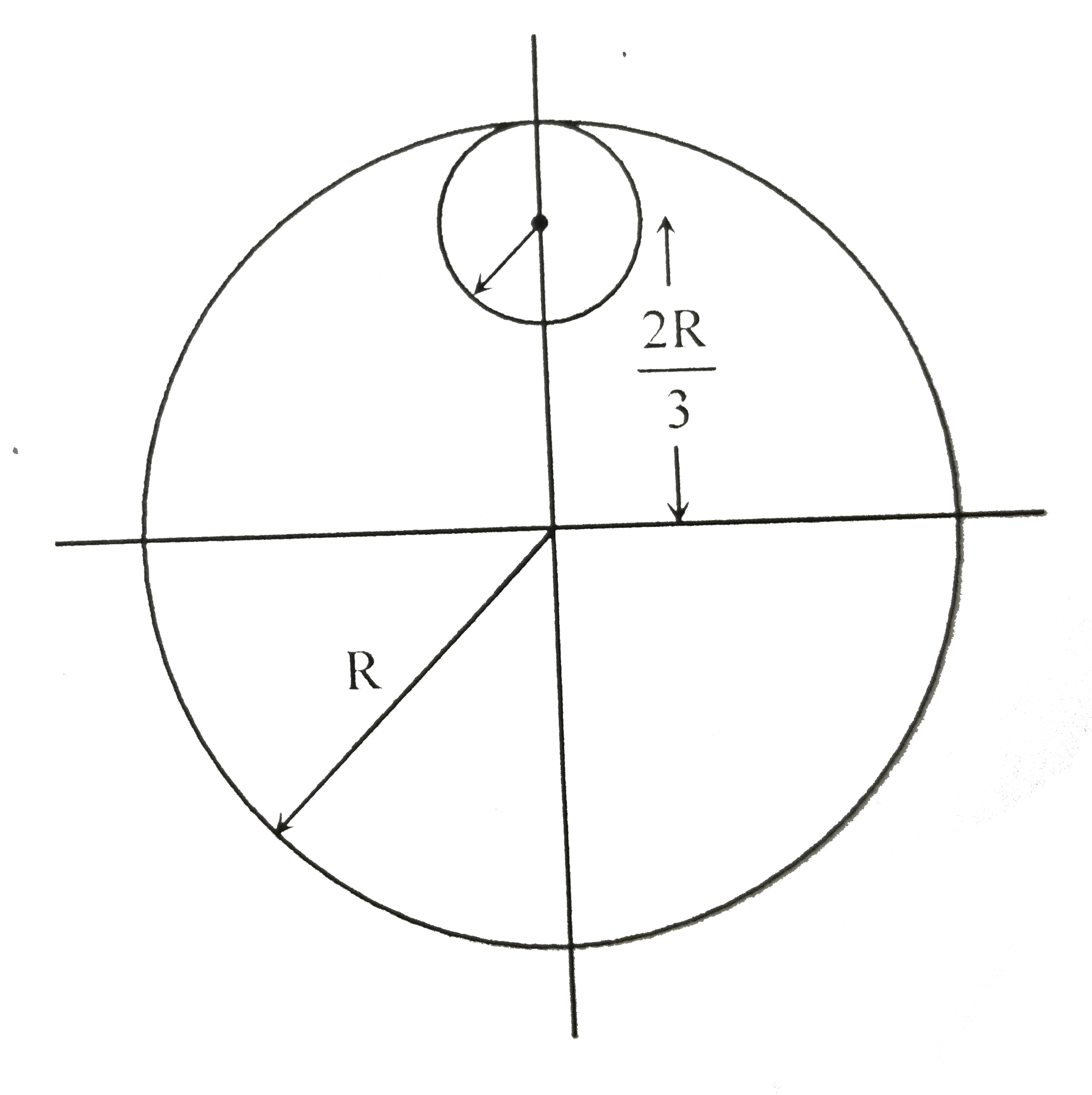A $4 M R^{2}$
B $\frac{40}{9} M R^{2}$
C $40 M R^{2}$
D $\frac{37}{9} M R^{2}$

VMC MODULES ENGLISH-ROTATIONAL MOTION -JEE MAIN (ARCHIVE)

Home
Ask Doubt
Profile