Two discs A and B are mounted coaxially on a vertical axle. The discs have moments of inertia I and 2I, respectively, about the common axis. Disc A is imparted an initial angular velocity 2w using the entire potential energy of a spring compressed by a distance x1. Disc B is imparted an angular velocity ω by a spring having the same spring constant and compressed by a distance x2. Both the discs rotate in the clockwise direction.
The loss of kinetic energy during the above process is
Iω22
Iω23
Iω24
Iω26
The correct Answer is:B
KEi−KEf⇒12I(2ω)2+123Iω21=13Iω2
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (ASSERTION & REASON TYPE)
2 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (MATRIX MATCH TYPE)
1 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (MULTIPLE OPTIONS CORRECT TYPE)
17 Videos
- REVISION TEST-2 JEEBOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS
25 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
Similar Questions
Two discs A and B are mounted coaxially ona vertical axle. The discs have moments of inertia l and 2l respectively about the common axis. Disc A is imparted an initial angular velocity 2ω using the centre potential energy of a spring compressed by a distance x1. Disc B is imparted angular velocity ω by a spring having the same spring constant and compressed by a distance x2. Both the disc rotate in the clockwise direction.
The loss of kinetic energy the above process is -
View SolutionTwo discs A and B are mounted co-axially one vertical axle. The discs have moments of inertia l and 2l respectively about the common axis. Disc A is imparted an initial angular velocity 2ω using the centre potential energy of a spring compressed by a distance x1. Disc B is imparted angular velocity ω by a spring having the same spring constant and compressed by a distance x2. Both the disc rotate in the clockwise direction.
The rotation x1/x2 is.
View SolutionTwo discs A and B are mounted coaxiallay on a vertical axle. The discs have moments of inertia I and 2 I respectively about the common axis. Disc A is imparted an initial angular velocity 2ω using the entire potential energy of a spring compressed by a distance x1 Disc B is imparted an angular velocity ω by a spring having the same spring constant and compressed by a distance x2 Both the discs rotate in the clockwise direction.
When disc B is brought in contact with disc A, they acquire a common angular velocity in time t. The average frictional torque on one disc by the other during this period is
View SolutionTwo bodies have their moments of inertia I and 2I, respectively about their axis of rotation. If their kinetic energies of rotation are equal, their angular velocity will be in the ratio
View SolutionA disc is rotating with angular velocity ω. If a child sits on it, what is conserved?
View SolutionIf I, α and τ are the moment of inertia, angular acceleration and torque respectively of a body rotating about an axis with angular velocity ω then,
View Solution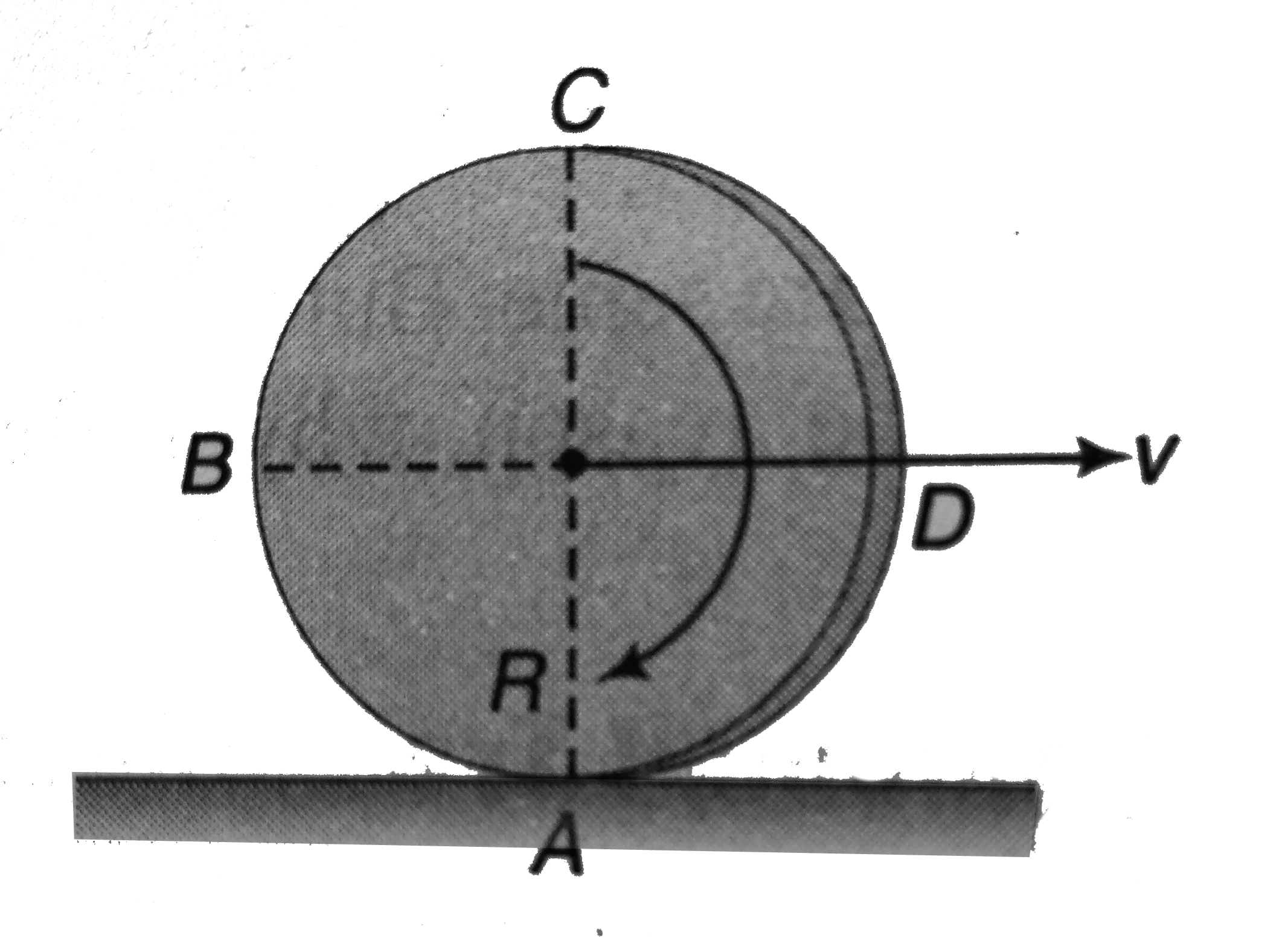
A disc of radius R has linear velocity v and angular velocity ω as shown in the figure. Given υ=rω find velocity of point A, B, C and D on the disc.
View SolutionA spring is stretched by distance x and then compressed to same distance from its original length. The work done by the spring force is (k=spring constant)
View SolutionTwo discs A and B have same mass and same thickness. If d1 and d2 are the densities of the materials of the discs A and B respectively, then the ratio of the moment of inertia of the discs A and B about their geometrical axis is
View SolutionTwo discs of same moment of inertia rotating about their regular axis passing through centre and perpendicular to the plane of disc with angular velocities ω1 and ω2. They are brought into contact face to face coinciding the axis of rotation. The expression for loss of energy during this process is
View Solution
