There is a uniform spherically symmetric surface charge density at a distance R0 from the origin . The charge distribution is intially at rest and starts expanding because of mutual repulsion , the figure that repeesents best the speed V (r(t)) of the distribution as a function of its instant radius R(t) is :
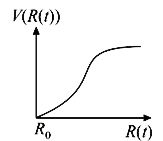
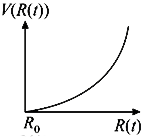
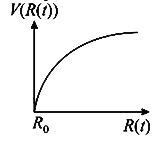

The correct Answer is:C
To solve the problem, we need to analyze the behavior of a uniformly charged spherical surface as it expands due to mutual repulsion. We'll derive the relationship between the speed V(r(t)) of the charge distribution and its instantaneous radius R(t).
1. Understanding the System:
- We have a uniform spherical surface charge density at a distance R0 from the origin.
- The charge distribution is initially at rest and begins to expand due to the mutual electrostatic repulsion between the charges.
2. Energy Conservation:
- The total energy of the charge distribution remains constant during the expansion.
- The total energy E can be expressed as the sum of kinetic energy K and potential energy U:
E=K+U
3. Kinetic Energy:
- The kinetic energy K of the charge distribution can be expressed as:
K=12mv2
- Here, m is the mass of the charge distribution and v is the speed of the charge distribution.
4. Potential Energy:
- The potential energy U due to the electrostatic interaction can be given by:
U=−kQ2R
- Where k is Coulomb's constant and Q is the total charge.
5. Setting Up the Energy Equation:
- At the initial state (when the radius is R0):
E=12mv2+U
- At the final state (when the radius is R(t)):
E=0+U=−kQ2R0
6. Equating Energies:
- Since total energy is conserved, we can write:
12mv2−kQ2R=−kQ2R0
- Rearranging gives:
12mv2=−kQ2R+kQ2R0
7. Solving for Velocity:
- We can express the velocity v in terms of R:
mv2=2kQ2(1R0−1R)
- Thus,
v=√2kQ2m(1R0−1R)
8. Analyzing the Function:
- As the radius R increases, the term (1R0−1R) decreases, which means that v decreases as R increases.
- Therefore, v(R) is a decreasing function of R.
9. Choosing the Correct Graph:
- From the analysis, we conclude that the speed v(R) decreases as the radius R increases.
- Among the given options, we look for a graph that shows a decreasing trend as R increases.
Conclusion:
Based on the analysis, the correct option that represents the speed V(r(t)) as a function of the instantaneous radius R(t) is Graph C, which shows a decreasing trend.
- We have a uniform spherical surface charge density at a distance R0 from the origin.
- The charge distribution is initially at rest and begins to expand due to the mutual electrostatic repulsion between the charges.
- The total energy of the charge distribution remains constant during the expansion.
- The total energy E can be expressed as the sum of kinetic energy K and potential energy U:
E=K+U
- The kinetic energy K of the charge distribution can be expressed as:
K=12mv2
- Here, m is the mass of the charge distribution and v is the speed of the charge distribution.
- The potential energy U due to the electrostatic interaction can be given by:
U=−kQ2R
- Where k is Coulomb's constant and Q is the total charge.
- At the initial state (when the radius is R0):
E=12mv2+U
- At the final state (when the radius is R(t)):
E=0+U=−kQ2R0
- Since total energy is conserved, we can write:
12mv2−kQ2R=−kQ2R0
- Rearranging gives:
12mv2=−kQ2R+kQ2R0
- We can express the velocity v in terms of R:
mv2=2kQ2(1R0−1R)
- Thus,
v=√2kQ2m(1R0−1R)
- As the radius R increases, the term (1R0−1R) decreases, which means that v decreases as R increases.
- Therefore, v(R) is a decreasing function of R.
- From the analysis, we conclude that the speed v(R) decreases as the radius R increases.
- Among the given options, we look for a graph that shows a decreasing trend as R increases.
Based on the analysis, the correct option that represents the speed V(r(t)) as a function of the instantaneous radius R(t) is Graph C, which shows a decreasing trend.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)
89 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 2
60 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Videos
Similar Questions
There is a uniform spherically symmetric surface charge density at a distance R0 from the origin . The charge distribution is intially at rest and starts expanding because of mutual repulsion , the figure that repeesents best the speed V (r(t)) of the distribution as a function of its intantanradius R(t) is :
View SolutionThe maximum surface charge density of a uniformly charged spherical radius R and wall thickness 't', so that it will not burst apart, is
View SolutionFor spherically symmetrical charge distribution, electric field at a distance r from the centre of sphere is →E=kr7→r, where k is a constant. What will be the volume charge density at a distance r from the centre of sphere?
View SolutionThe energy density u is plotted against the distance r from the centre of a spherical charge distribution on a log-log scale. Find the magnitude of slope of obtained straight line.
View SolutionAn insulating solid sphere of radius R has a uniformly positive charge density ρ. As a result of this uniform charge distribution there is a finite value of electric potential at the centre of the sphere, at the surface of the sphere and also at a point out side the sphere. The electric potential at infinity is zero.
Statement-1: When a charge 'q' is taken from the centre to the surface of the sphere, its potential energy changes by qρ3∈0
Statement-2 : The electric field at a distance r(r<R) from the centre of the the sphere is ρr3∈0
View SolutionA long thin flat sheet has a uniform surface charge density σ. The magnitude of the electric field at a distance .r. from it is given by
View SolutionA positive charge is released from rest at a distance r0 from a positive line charge with uniform density . The speed (v) of the point charge , as a function of instantaneous distance r from line charge, is proportional to:
View SolutionConsider a uniform spherical charge distribution of radius R1 centred at the origin O. In this distribution a spherical cavity of radius R2, centred at P with distance OP=a=R1−R2 (fig) is made.If the electric field inside the cavity at position →r, then the correct statement is
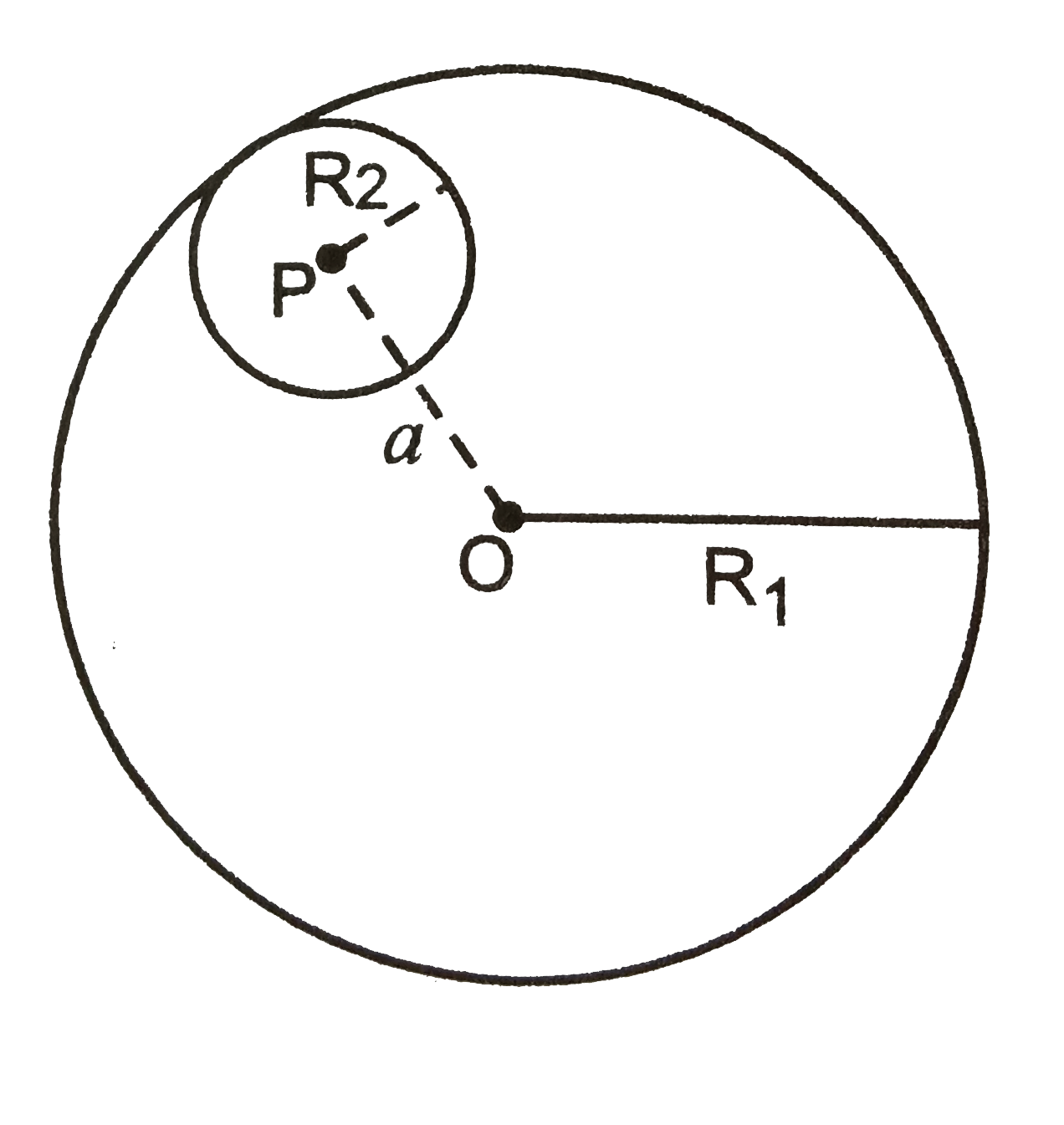
View SolutionLet there be a spherical symmetric charge density varying as p(r)=p0rR upto r = R and ρ(r)=0 for r>R, where r is the distance from the origin. The electric field at on a distance r(r<R) from the origin is given by -
View SolutionFind the electric field due to an infinitely long cylindrical charge distribution of radius R and having linear charge density λ at a distance half of the radius from its axis.
View Solution
