A particle A of charge 1μC is held fixed at a point P in free space . Another particle B of same charge and mass 4μg is kept at a distance of1mm from P .If B is released then its velocity at a distance of 9 mm from P is (Take 14πε0=9×109Nm2C−2)
2.0×103m/s
1.5×102m/s
3.0×104m/s
1.0m/s
To solve the problem step by step, we will use the principle of conservation of mechanical energy. The total mechanical energy (potential energy + kinetic energy) remains constant since there are no external forces acting on the system.
Step 1: Understand the Initial Conditions
- Particle A has a charge QA=1μC=1×10−6C and is fixed at point P.
- Particle B has the same charge QB=1μC=1×10−6C and mass m=4μg=4×10−9kg.
- Particle B is initially at a distance ri=1mm=1×10−3m from P and is released from rest.
Step 2: Write the Conservation of Energy Equation
The total mechanical energy at the initial position (when B is released) is equal to the total mechanical energy when B is at a distance of rf=9mm=9×10−3m.
Ui+Ki=Uf+Kf
Where:
- U is the potential energy
- K is the kinetic energy
Since B is released from rest, the initial kinetic energy Ki=0. Therefore, the equation simplifies to:
Ui=Uf+Kf
Step 3: Calculate the Initial Potential Energy Ui
The potential energy U between two point charges is given by:
U=14πϵ0⋅QAQBr
Substituting the values for Ui:
Ui=14πϵ0⋅(1×10−6)21×10−3=9×109⋅1×10−121×10−3=9×10−3J
Step 4: Calculate the Final Potential Energy Uf
Now calculate Uf at rf=9mm:
Uf=14πϵ0⋅(1×10−6)29×10−3=9×109⋅1×10−129×10−3=1×10−3J
Step 5: Substitute into the Energy Equation
Substituting Ui and Uf into the energy conservation equation:
9×10−3J=1×10−3J+Kf
Solving for Kf:
Kf=9×10−3J−1×10−3J=8×10−3J
Step 6: Relate Kinetic Energy to Velocity
The kinetic energy Kf is given by:
Kf=12mv2
Substituting the values:
8×10−3=12⋅(4×10−9)v2
Step 7: Solve for Velocity v
Rearranging the equation to solve for v2:
v2=8×10−3⋅24×10−9=16×10−34×10−9=4×106
Taking the square root to find v:
v=√4×106=2×103m/s
Final Answer
The velocity of particle B at a distance of 9 mm from point P is 2×103m/s.
---
- Particle A has a charge QA=1μC=1×10−6C and is fixed at point P.
- Particle B has the same charge QB=1μC=1×10−6C and mass m=4μg=4×10−9kg.
- Particle B is initially at a distance ri=1mm=1×10−3m from P and is released from rest.
The total mechanical energy at the initial position (when B is released) is equal to the total mechanical energy when B is at a distance of rf=9mm=9×10−3m.
- U is the potential energy
- K is the kinetic energy
The potential energy U between two point charges is given by:
Now calculate Uf at rf=9mm:
Substituting Ui and Uf into the energy conservation equation:
The kinetic energy Kf is given by:
Rearranging the equation to solve for v2:
The velocity of particle B at a distance of 9 mm from point P is 2×103m/s.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)
89 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - LEVEL - 2
60 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Videos
Similar Questions
The electric field due to a charge at a distance of 3 m from it is 500NC−1. The magnitude of the charge is
[14πε0=9×109N−m2/C2]
View SolutionA particle P of charge q and m , is placed at a point in gravity free to move. Another particle Q, of same charge and mass , is projected from a distance r from P with an initial speed v0 towards P , initial the distance between P and Q decreases and then increases.
The potential energy of the system of particles P and Q, at closest separation is
View SolutionA hollow sphere of radius 0.1 m has a charge of 5×10−8C. The potential at a distance of 5 cm from the centre of the sphere is
(14πε0=9×109Nm2C−2)
View SolutionThree particles, each having a charge of 10μC are placed at the coners of an equilateral triangle of side 10cm. The electrostatic potential energy of the system is (Given 14πε0=9×109N−m2/C2)
View SolutionTwo charge particle P&Q having same charge 1μC and mass 4μkg are initially kept at the distance of 1mm. Charge P is fixed, then the velocity of charge parti Q when the separationbetween then becmoes 9mm.
_2019_CBT6_E01_048_Q01.png)
View SolutionTwo charges of 4μC each are placed at the corners A and B of an equilaternal triangle of side length 0.2m in air. The
electric potential at C is [14πε0=9×109N−m2C2]
View SolutionA particle of mass 2 g and charge 1μC is held at rest on a frictionless surface at a distance of 1m from a fixed charge of 1 mC. If the particle is released it will be repelled. The speed of the particle when it is at distance of 10 m from fixed charge is :
View SolutionIn the rectangle, shown below, the two corners have charges q1=−5μC and q2=+2.0μC. The work done in moving a charge +3.0μC from B→A is (take 1/44πε0=1010N−m2/C2)
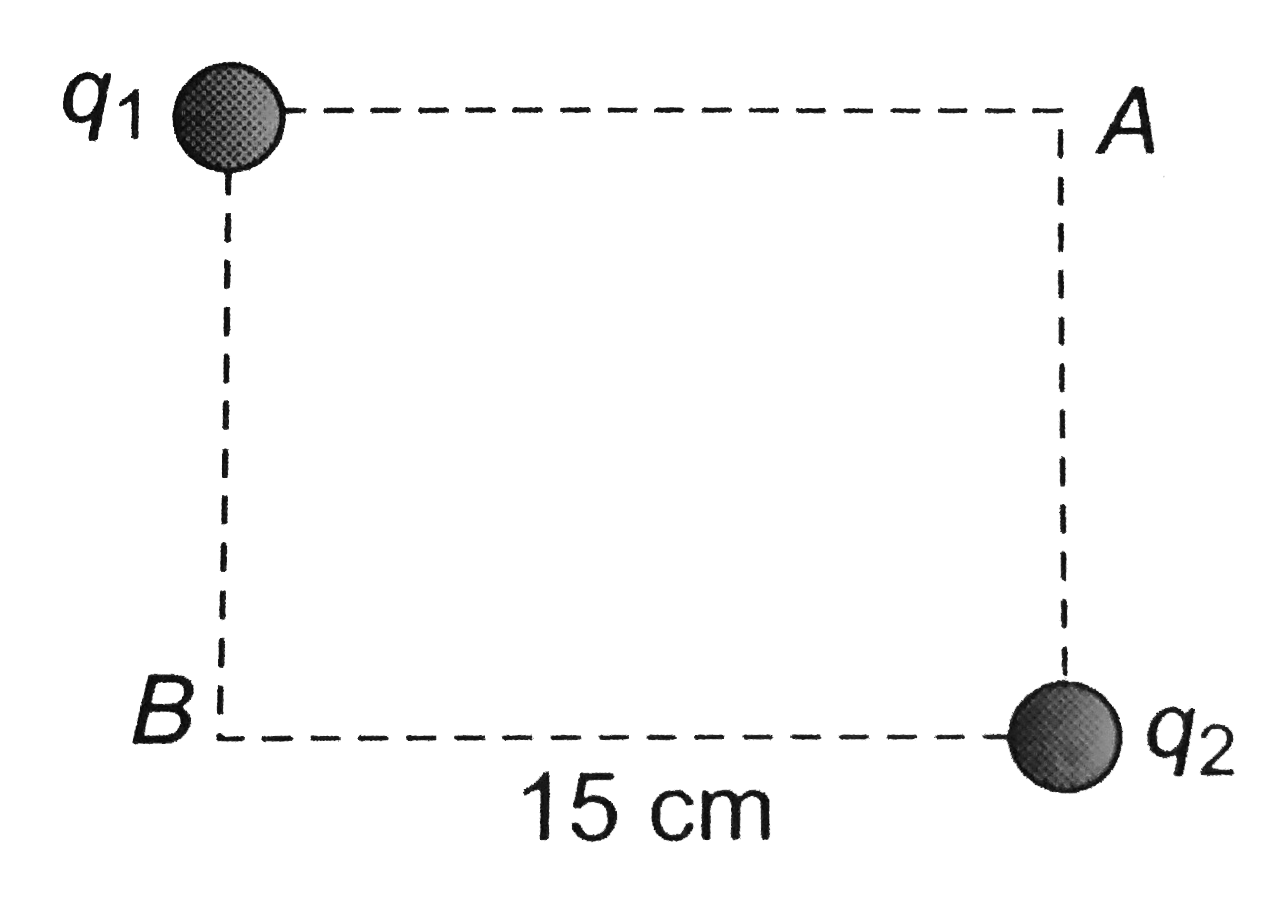
View SolutionTwo identical charges, 5μC each are fixed at a distance 8 cm and a charged particle of mass 9×10−6kg and charge −10μC is placed at a distance 5 cm from each of them and is released. Find the speed of the particle when it is nearest to the two charges.
View SolutionWhat is the magnitude of a point charge due to which the electric field 30cm away the magnitude 2?
[1/4πε0=9×109Nm2/C2]
View Solution
