A body moves in a straight line along Y-axis. Its distance y in metre) from the origin is given y=8t−3t2. The average speed in the time interval from t=0 second to t=1 second is
−4ms−1
Zero
5ms−1
6ms−1
The correct Answer is:C
To find the average speed of the body moving along the Y-axis given the equation y=8t−3t2, we will follow these steps:
Step 1: Understand the average speed formula
The average speed is defined as the total distance traveled divided by the total time taken. Mathematically, it can be expressed as:
Average Speed=Total DistanceTotal Time
Step 2: Determine the time interval
We need to calculate the average speed from t=0 seconds to t=1 second. Therefore, the total time Δt is:
Δt=1−0=1 second
Step 3: Calculate the position at t=0
Substituting t=0 into the equation y=8t−3t2:
y(0)=8(0)−3(0)2=0 meters
Step 4: Calculate the position at t=1
Now, substituting t=1 into the same equation:
y(1)=8(1)−3(1)2=8−3=5 meters
Step 5: Calculate the total distance traveled
The total distance traveled from t=0 to t=1 is:
Total Distance=y(1)−y(0)=5−0=5 meters
Step 6: Calculate the average speed
Now, we can calculate the average speed using the values we found:
Average Speed=Total DistanceTotal Time=5 meters1 second=5 meters per second
Conclusion
Thus, the average speed of the body in the time interval from t=0 seconds to t=1 second is:
Average Speed=5 m/s
The average speed is defined as the total distance traveled divided by the total time taken. Mathematically, it can be expressed as:
We need to calculate the average speed from t=0 seconds to t=1 second. Therefore, the total time Δt is:
Substituting t=0 into the equation y=8t−3t2:
Now, substituting t=1 into the same equation:
The total distance traveled from t=0 to t=1 is:
Now, we can calculate the average speed using the values we found:
Thus, the average speed of the body in the time interval from t=0 seconds to t=1 second is:
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE & PLANE BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - ENABLE
50 Videos
- MOTION IN A STRAIGHT LINE & PLANE BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - EFFICIENT
50 Videos
- MOCK TEST 9BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 9EXERCISE - PHYSICS (SECTION 2)
5 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-J
10 Videos
Similar Questions
A particle moves along a straight line on y-axis. The distance of the particle from O varies with time and is given by : y=20t−t2. The distance travelled by the particle before it momentarily comes to rest is
View SolutionA point mives in a straight line so its displacement x mertre at time t second is given by x2=1+t2. Its aceleration in ms−2 at time t second is .
View SolutionA particle moves along a straight line OX. At a time t (in seconds) the distance x (in metre) of the particle is given by x=40+12t−t3. How long would the particle travel before coming to rest ?
View SolutionA particle moves along a straight line OX. At a time t(in second), the distance x (in metre) of the particle from O is given by
x=40+12t−t3
How long would the particle travel before coming to rest ?
View SolutionA body moves along x-axis such that its displacement varies with time as given, x=7+3t+5t2. The average velocity during 3rd second is
View SolutionThe displacement (in metre) of a particle moving along X-axis is given by x=18t+5t2. The average acceleration during the interval t1=2s and t2=4s is
View SolutionIf velocity of a partical moving along a straight line changes sinusoidally with time as shown in given graph. Find the average speed over time interval t=0 to t=2(2n−1) second, n being any positive interget.
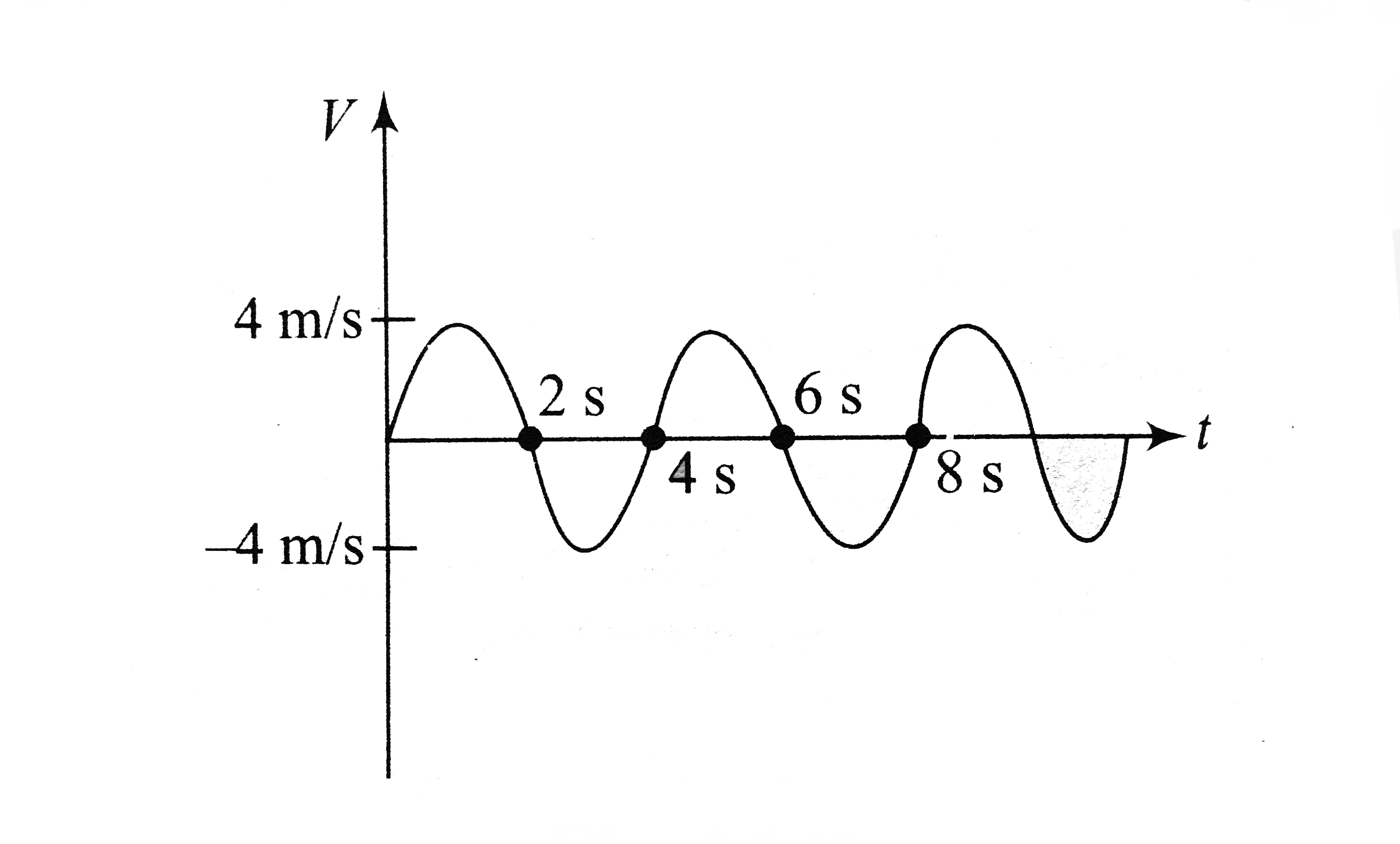
View SolutionIf velocity of a partical moving along a straight line changes sinusoidally with time as shown in given graph. Find the average speed over time interval t=0 to t=2(2n−1) second, n being any positive interget.
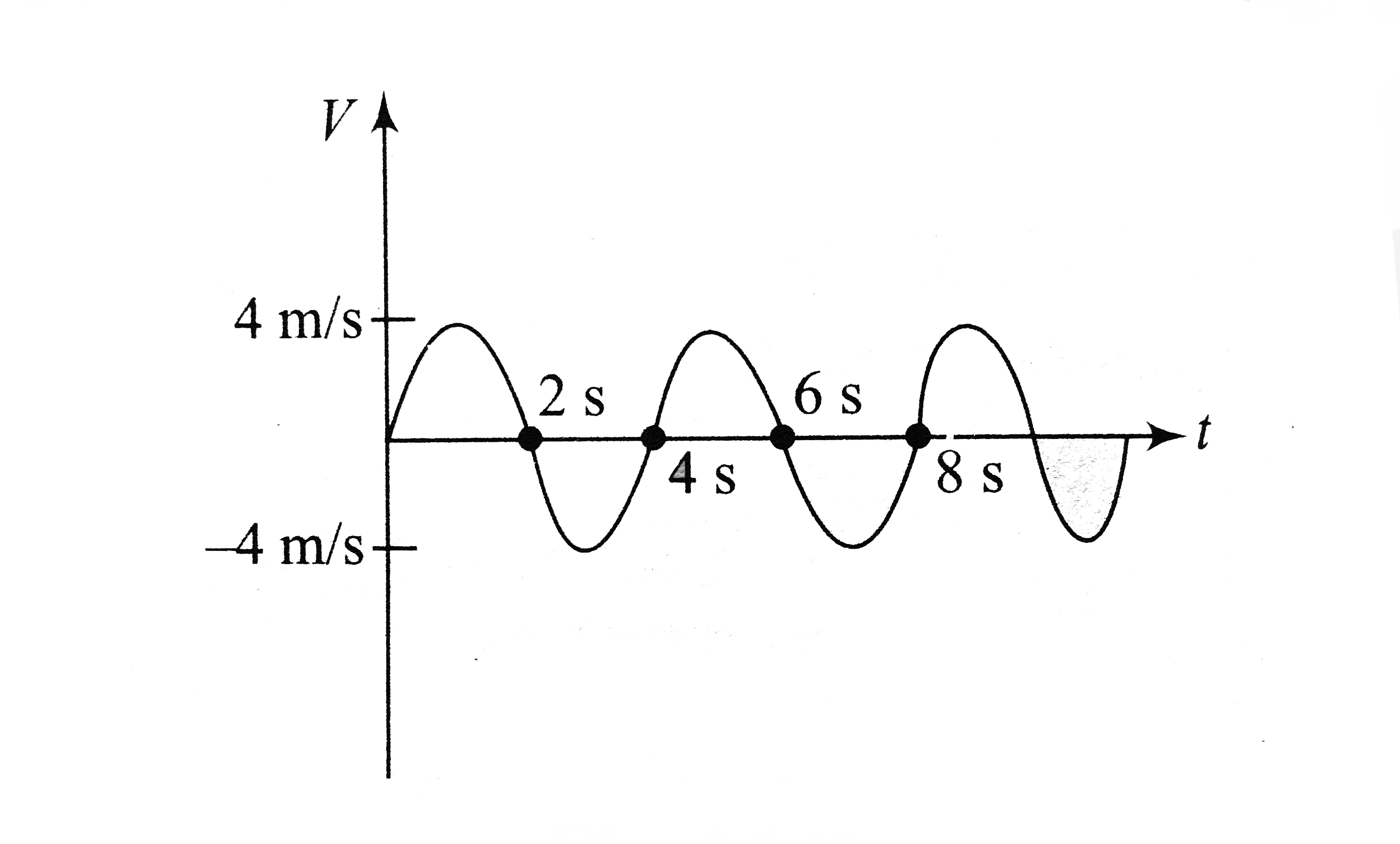
View SolutionA particle moves along a straight line. At a time t (in seconds) the distance x (in meter) of the particle is given by x=13t3+3t2−7t. How long would the particle travel before coming to rest ?
View SolutionThe position of a particle along X-axis at time t is given by x=2+t−3t2. The displacement and the distance travelled in the interval, t = 0 to t = 1 are respectively
View Solution
