The Bernoulli's equation is given by P+12ρv2+hρg=k. Where P= pressure, ρ= density, v= speed, h=height of the liquid column, g= acceleration due to gravity and k is constant. The dimensional formula for k is same as that for:
Velocity gradient
Pressure gradient
Modulus of elasticity
Thrust
The correct Answer is:C
To find the dimensional formula for k in Bernoulli's equation, we start by analyzing the equation itself:
P+12ρv2+ρgh=k
Where:
- P = pressure
- ρ = density
- v = speed
- h = height of the liquid column
- g = acceleration due to gravity
- k = constant
Step 1: Determine the dimensions of each term in the equation.
1. Pressure (P):
- Pressure is defined as force per unit area.
- The dimensional formula for force is (MLT−2) (mass × acceleration).
- The area has the dimensional formula (L2).
- Therefore, the dimensional formula for pressure is:
(P)=(MLT−2)(L2)=(ML−1T−2)
2. Kinetic Energy Density (12ρv2):
- The term 12 is a constant and does not affect dimensions.
- Density (ρ) has the dimensional formula (ML−3).
- Speed (v) has the dimensional formula (LT−1).
- Therefore, v2 has the dimensional formula (L2T−2).
- Now, the dimensional formula for ρv2 is:
(ρv2)=(ML−3)⋅(L2T−2)=(ML−1T−2)
3. Potential Energy Density (ρgh):
- The acceleration due to gravity (g) has the dimensional formula (LT−2).
- Height (h) has the dimensional formula (L).
- Therefore, the dimensional formula for ρgh is:
(ρgh)=(ML−3)⋅(LT−2)⋅(L)=(ML−1T−2)
Step 2: Combine the terms.
Since all the terms P, 12ρv2, and ρgh have the same dimensional formula (ML−1T−2), we can conclude that:
k must also have the same dimensional formula as these terms.
Step 3: Conclusion.
Thus, the dimensional formula for k is:
(k)=(ML−1T−2)
Step 4: Compare with the options.
Now, we need to check which of the given options has the same dimensional formula as k.
1. Velocity Gradient: This has dimensions of (T−1) which is not the same as (ML−1T−2).
2. Pressure Gradient: This has dimensions of (ML−2T−2) which is not the same as (ML−1T−2).
3. Modulus of Elasticity: This has dimensions of (ML−1T−2) which is the same as k.
4. Thrust: This has dimensions of (MLT−2) which is not the same as (ML−1T−2).
Final Answer:
The correct option is C: Modulus of Elasticity.
---
- P = pressure
- ρ = density
- v = speed
- h = height of the liquid column
- g = acceleration due to gravity
- k = constant
- Pressure is defined as force per unit area.
- The dimensional formula for force is (MLT−2) (mass × acceleration).
- The area has the dimensional formula (L2).
- Therefore, the dimensional formula for pressure is:
(P)=(MLT−2)(L2)=(ML−1T−2)
- The term 12 is a constant and does not affect dimensions.
- Density (ρ) has the dimensional formula (ML−3).
- Speed (v) has the dimensional formula (LT−1).
- Therefore, v2 has the dimensional formula (L2T−2).
- Now, the dimensional formula for ρv2 is:
(ρv2)=(ML−3)⋅(L2T−2)=(ML−1T−2)
- The acceleration due to gravity (g) has the dimensional formula (LT−2).
- Height (h) has the dimensional formula (L).
- Therefore, the dimensional formula for ρgh is:
(ρgh)=(ML−3)⋅(LT−2)⋅(L)=(ML−1T−2)
2. Pressure Gradient: This has dimensions of (ML−2T−2) which is not the same as (ML−1T−2).
3. Modulus of Elasticity: This has dimensions of (ML−1T−2) which is the same as k.
4. Thrust: This has dimensions of (MLT−2) which is not the same as (ML−1T−2).
Topper's Solved these Questions
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - Impeccable
51 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - Illustration
24 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - Enable
50 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE
56 Videos
- WAVE MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (TRUE FALSE TYPE)
4 Videos
Similar Questions
If pressure P, velocity of light c and acceleration due to gravity g are chosen as fundamental units, then dimensional formula of mass is
View SolutionIf pressure P, velocity of light C and acceleration due to gravity g are chosen as fundamental units, then dimensional formula of mass is
View Solution
Knowledge Check
The radii of two planets are respectively R1andR2 and their densities are respectively ρ1andρ2.The ratio of the accelerations due to gravity at their surface is
AR1ρ2R2ρ1BR1ρ1R2ρ2Cρ1R22ρ2R21DR1R2ρ1ρ2The density of the core a planet is ρ1 and that of the outer shell is ρ2. The radii of the core and that of the planet are R and 2R respectively. The acceleration due to gravity at the surface of the planet is same as at a depth R. Find the ratio of ρ1ρ2
 A2.3B4.5C3.2D5.4
A2.3B4.5C3.2D5.4
According to Bernoullis theoram pd+v22+gh = constant, dimensional formula of the constant.
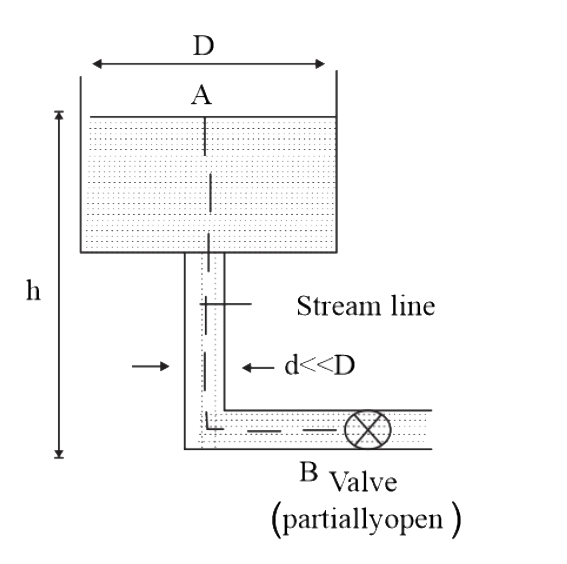
View SolutionA storage tower supplies water, as shown in the figure. If P0 is the atmospheric pressure h = height of water level, g = acceleration due to gravity, ρ= density and v = velocity of flow in the horizontal pipe at B, then the pressure at B is -
View SolutionThe absolute pressure at a depth h below the surface of a liquid of density ρ is [Given Pa = atmospheric pressure, g = acceleration due to gravity]
View SolutionThe density of the core a planet is ρ1 and that of the outer shell is ρ2. The radii of the core and that of the planet are R and 2R respectively. The acceleration due to gravity at the surface of the planet is same as at a depth R. Find the radio of ρ1ρ2

View SolutionThe density of the core a planet is ρ1 and that of the outer shell is ρ2. The radii of the core and that of the planet are R and 2R respectively. The acceleration due to gravity at the surface of the planet is same as at a depth R. Find the ratio of ρ1ρ2

View Solution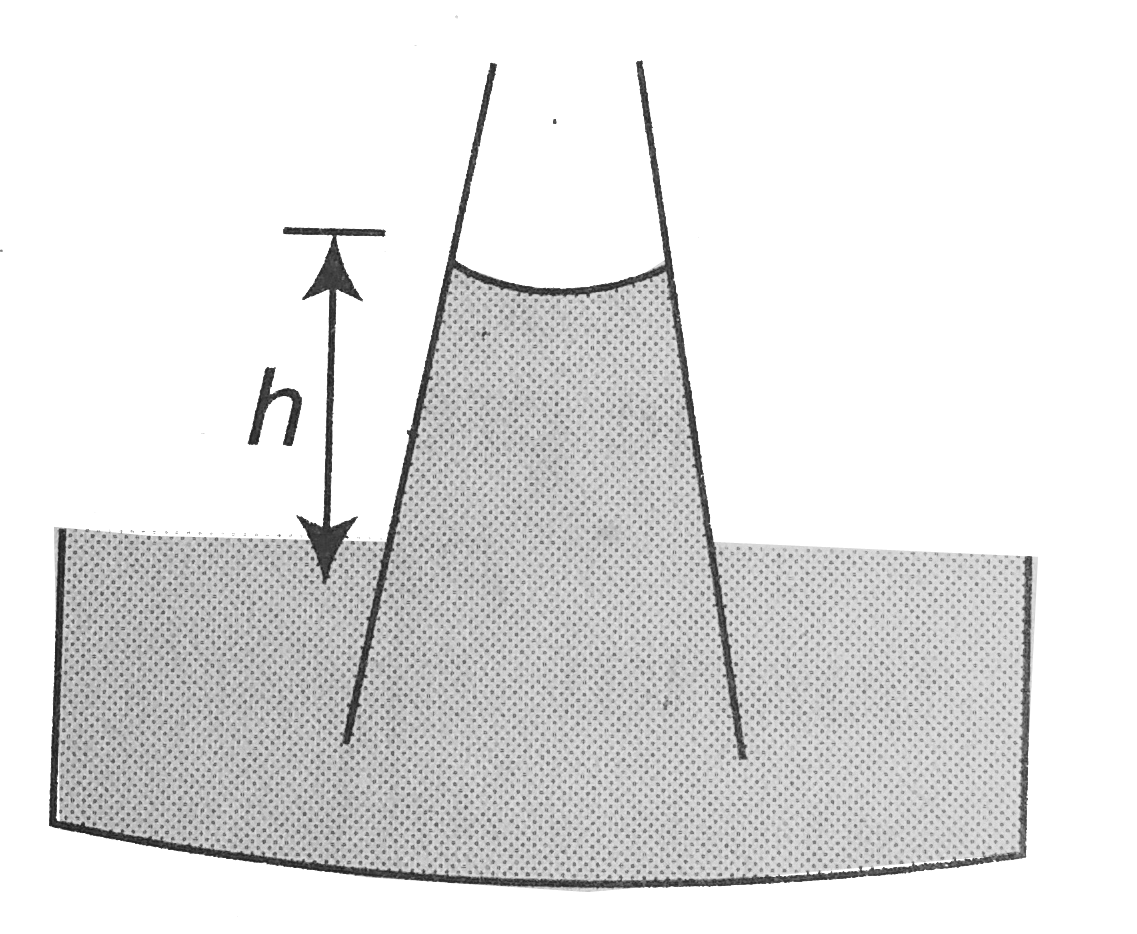
A capillary of the shape as shown is dipped in a liquid. Contact angle between the liquid and the capillary is 0∘ and effect of liquid inside the mexiscus is to be neglected. T is surface tension of the liquid, r is radius of the meniscus, g is acceleration due to gravity and ρ is density of the liquid then height h in equilibrium is:
View Solution
