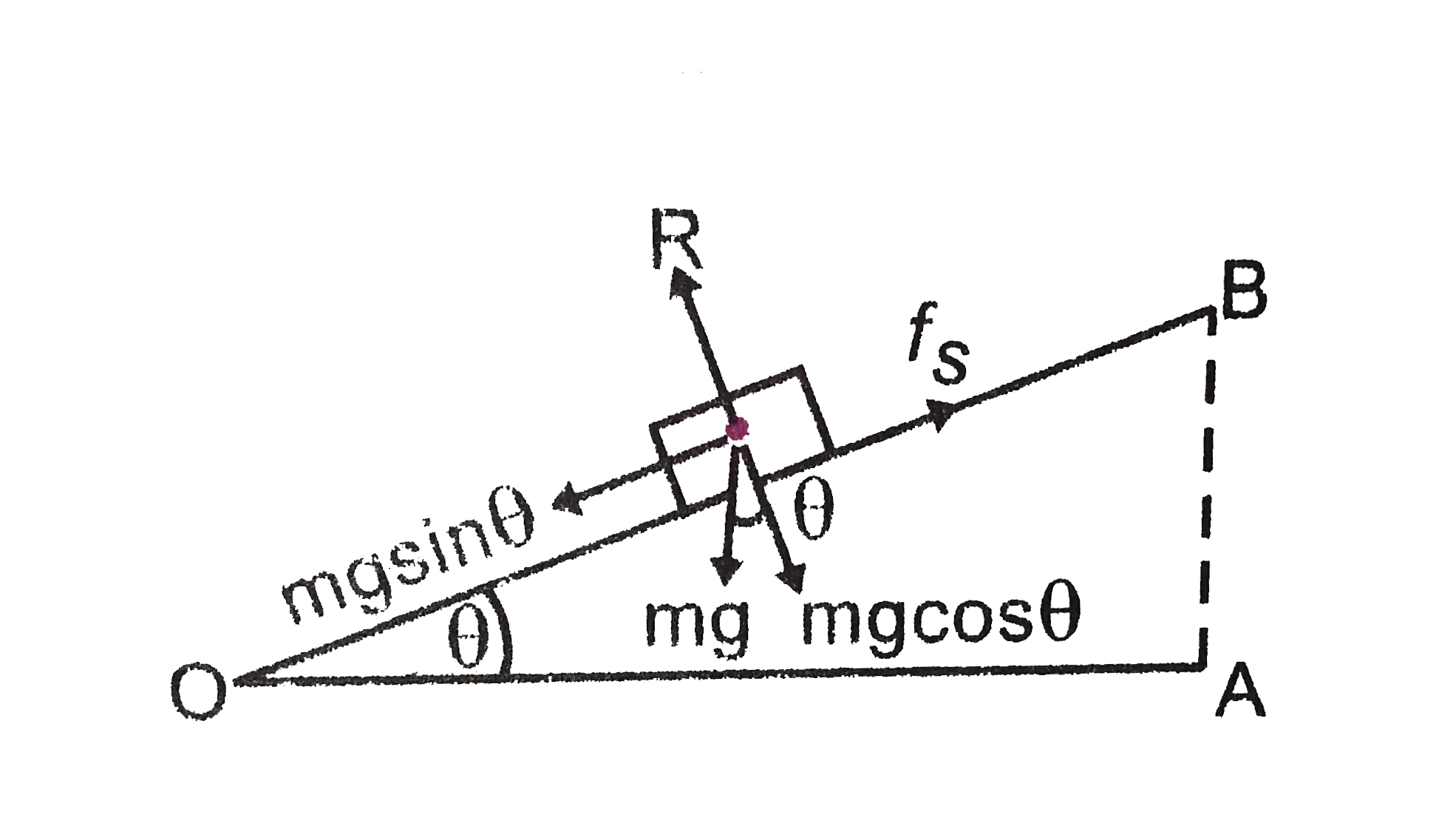
A block of mass 4kg rests on an an inclined plane. The inclination of the plane is gradually increased. It is found that when the inclination is 3 in 5 (sin=θ35) the block just begins to slide down the plane. The coefficient of friction between the block and the plane is.
0.4
0.6
0.8
0.75
The correct Answer is:4
To find the coefficient of friction between the block and the inclined plane, we will follow these steps:
Step 1: Understanding the Problem
We have a block of mass m=4kg resting on an inclined plane. The inclination angle θ is such that sinθ=35. We need to find the coefficient of friction μ when the block just begins to slide down.
Step 2: Finding the Angle θ
Given that sinθ=35, we can use the Pythagorean theorem to find cosθ:
cos2θ=1−sin2θ
cos2θ=1−(35)2=1−925=1625
cosθ=45
Step 3: Finding tanθ
Now, we can find tanθ:
tanθ=sinθcosθ=3545=34
Step 4: Relating tanθ to the Coefficient of Friction
The angle θ at which the block begins to slide is also the angle of repose. The relationship between the angle of repose and the coefficient of friction is given by:
tanθ=μ
Thus, we have:
μ=tanθ=34
Step 5: Conclusion
The coefficient of friction μ between the block and the inclined plane is:
μ=0.75
Final Answer
The coefficient of friction between the block and the plane is 0.75.
---
We have a block of mass m=4kg resting on an inclined plane. The inclination angle θ is such that sinθ=35. We need to find the coefficient of friction μ when the block just begins to slide down.
Given that sinθ=35, we can use the Pythagorean theorem to find cosθ:
cos2θ=1−sin2θ
cos2θ=1−(35)2=1−925=1625
cosθ=45
Now, we can find tanθ:
tanθ=sinθcosθ=3545=34
The angle θ at which the block begins to slide is also the angle of repose. The relationship between the angle of repose and the coefficient of friction is given by:
tanθ=μ
Thus, we have:
μ=tanθ=34
The coefficient of friction μ between the block and the inclined plane is:
μ=0.75
The coefficient of friction between the block and the plane is 0.75.
Topper's Solved these Questions
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - ENABLE
50 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - EFFICIENT
50 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)
14 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
Similar Questions
A block of mass 5 kg is placed on a rough inclined plane. The inclination of the plane is gradually increased till the block just begins to slide down. The inclination of the plane is than 3 in 5. The coefficient of friction between the block and the plane is (Take, g=10m/s2)
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View Solution
Knowledge Check
A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
Aθ=tan−1μBθ=cos−1μCθ=sin−1μDθ=sec−1μ
A block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View SolutionA block of mass 5 kg rests on a inclined plane at an angle of 30∘ with the horizontal. If the block just begins to slide, then what is the coefficient of static friction between the block and the surface?
View SolutionA block of mass m is kept on an inclined plane is angle inclination θ(<ϕ), where ϕ= angle of friction. Then :

View SolutionA block of mass 4kg rests on a rough horizontal plane. The plane is gradually inclined until at an angle θ=60∘ , with the vertical, the mass just begins to side. What is the coefficient of static friction between the block and the plane?
View SolutionA mass of 2kg rests on a horizontal plane. The plane is gradually inclined until at an angle θ=20∘ with the horizontal, the mass just begins to slides. What is the coefficient of static friction between the block and the surface ?
View SolutionIf the angle of inclination of the inclined plane is sin−1(12) when the body just starts sliding find the angle of repose and coefficient of static friction between the body and the inclined plane.
View SolutionA mass of 4 kg rest on a horizontal plane . The plane is gradually inclined until an angle 0=15∘ with the horizontal and the mass just begins to slide . What is the coefficient of static friction between the block and the surface ?
View Solution
