A boy standing on a weighing machine observes his weight as 200 N. When he suddenly jumpes upwards, his friend notices that the reading increased to 400 N. The acceleration by which the boy jumped will be-
(a)9.8m/s2
(b)29.4m/s2
(c)4.9m/s2
(d)14.7m/s2
The correct Answer is:1
To solve the problem, we need to analyze the forces acting on the boy when he jumps and how they relate to the readings on the weighing machine.
1. Understanding the Initial Condition:
- The boy is standing on the weighing machine, and the reading shows 200 N. This indicates that the weight of the boy (W) is 200 N.
- Weight (W) is given by the formula:
W=mg
- Here, m is the mass of the boy and g is the acceleration due to gravity (approximately 9.8m/s2).
2. Calculating the Mass of the Boy:
- From the weight equation, we can express the mass of the boy as:
m=Wg=200N9.8m/s2≈20.41kg
3. Understanding the Jump:
- When the boy jumps, the reading on the weighing machine increases to 400 N. This is the apparent weight when he is accelerating upwards.
- The apparent weight (normal force, N) when the boy jumps can be expressed as:
N=mg+ma
- Here, a is the upward acceleration of the boy.
4. Setting Up the Equation:
- We know that when he jumps, the normal force (N) becomes 400 N. Therefore, we can write:
400N=mg+ma
- Substituting mg with 200 N (the boy's weight):
400N=200N+ma
5. Solving for Acceleration (a):
- Rearranging the equation gives us:
ma=400N−200N=200N
- Now, substituting m (which we calculated as approximately 20.41 kg):
20.41kg⋅a=200N
- Solving for a:
a=200N20.41kg≈9.8m/s2
6. Conclusion:
- The acceleration by which the boy jumped is approximately 9.8m/s2.
Final Answer:
The acceleration by which the boy jumped is 9.8m/s2.
- The boy is standing on the weighing machine, and the reading shows 200 N. This indicates that the weight of the boy (W) is 200 N.
- Weight (W) is given by the formula:
W=mg
- Here, m is the mass of the boy and g is the acceleration due to gravity (approximately 9.8m/s2).
- From the weight equation, we can express the mass of the boy as:
m=Wg=200N9.8m/s2≈20.41kg
- When the boy jumps, the reading on the weighing machine increases to 400 N. This is the apparent weight when he is accelerating upwards.
- The apparent weight (normal force, N) when the boy jumps can be expressed as:
N=mg+ma
- Here, a is the upward acceleration of the boy.
- We know that when he jumps, the normal force (N) becomes 400 N. Therefore, we can write:
400N=mg+ma
- Substituting mg with 200 N (the boy's weight):
400N=200N+ma
- Rearranging the equation gives us:
ma=400N−200N=200N
- Now, substituting m (which we calculated as approximately 20.41 kg):
20.41kg⋅a=200N
- Solving for a:
a=200N20.41kg≈9.8m/s2
- The acceleration by which the boy jumped is approximately 9.8m/s2.
The acceleration by which the boy jumped is 9.8m/s2.
Topper's Solved these Questions
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - ENABLE
50 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - EFFICIENT
50 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)
14 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
Similar Questions
A man is standing on a weighing machine with a block in his hand. The machine records w. When he takes the block upwards with some acceleration the machine records w1. When he takes the block down with some acceleration, the machine records w2. Then choose correct option
View SolutionA man is standing on a weighing machine placed in a lift. When stationary his weight is recorded as 40 kg . If the lift is accelerated upwards with an acceleration of 2m/s2 , then the weight recorded in the machine will be (g=10m/s2)
View SolutionFigure shows a man of mass 60 kg standing on a light weighting machine kept in a box of mass 30 kg. The box is hanging from a pulley fixed to the ceiling through a light rope, the other end of which is held by the man himself. If the man manages to keep the box at rest, what is the weight shown by the machine? What force should he exert on the rope to get his correct weight on the machine?
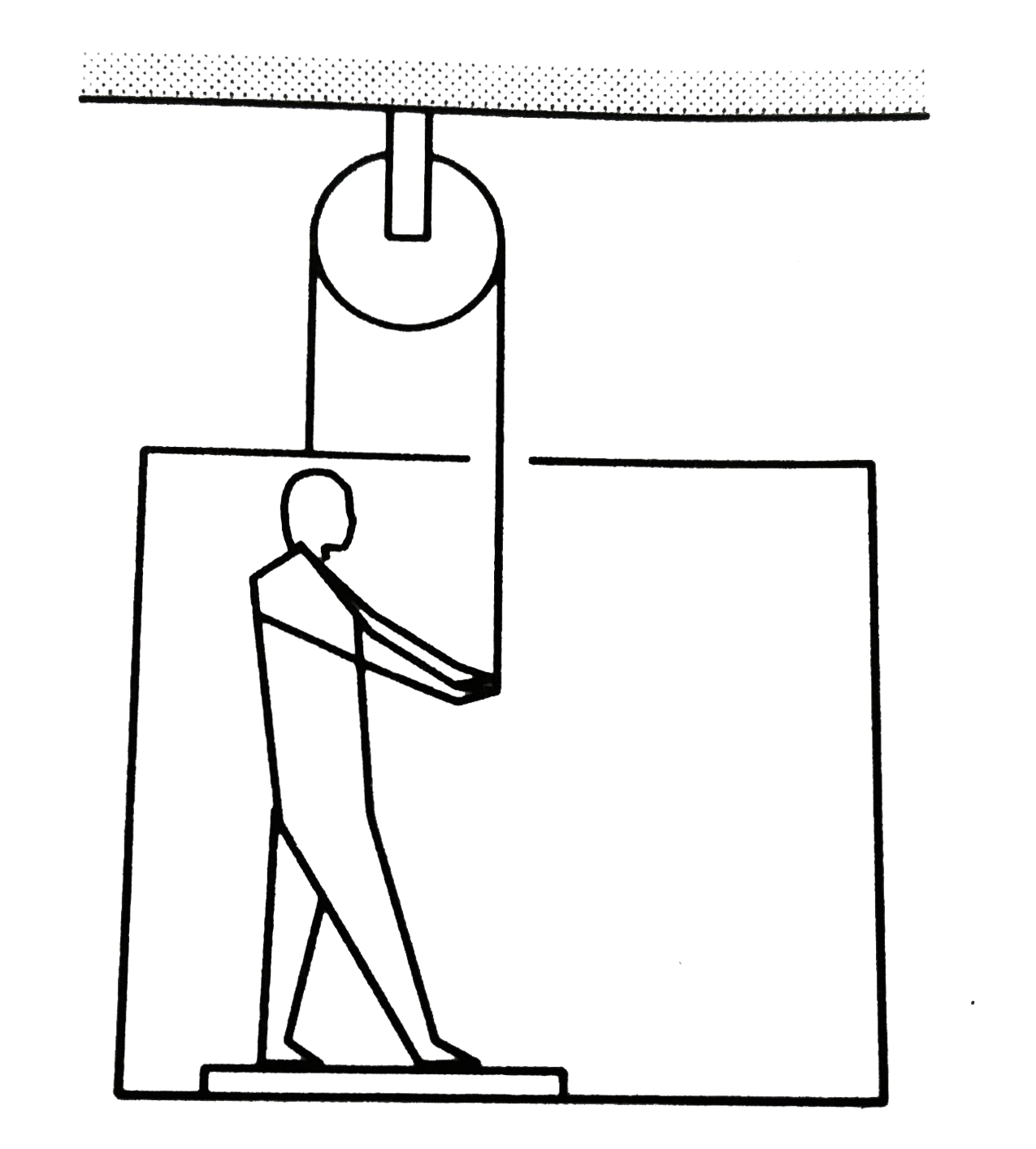
View SolutionA boy standing in front of a wall at a distance of 85 m produces 2 claps per second. He notices that the sound of his clapping coincides with the echo. The echo is heard only once when clapping is stopped. Calculate the speed of sound.
View SolutionA man of mass M stands on a weighing machine in an elevator accelerating upwards with an acceleration a. Draw the free-body diagram of the man as observed by the observer A (stationary on the ground) and observer B (stationary on the elevator). Also, calculate the reading of the weighing machine.

View SolutionA body of mass 40 kg stands on a weighing machine in an accelerated lift. The reading on the scale of the weighing machine is 300 N. Find the magnitude and direction of acceleration. (g=9.8ms−2)
View SolutionA person is standing in an elevator. In which situation he finds his weight less than actual when:
View SolutionA man of mass 40kg is standing on a weighting machine kept on the floor of an elevator which is moving up with an acceleration of 2m/s2 Find the reading of the weighing maching.

View SolutionA man of mass 40kg is standing on a weighting machine kept on the floor of an elevator which is moving up with an acceleration of 2m/s2 Find the reading of the weighing maching.

View Solutiona. A rail road flat car of mass M can roll without friction along a straight horizontal track . Initially, a man of mass m is standing on the car which is moving to the right with speed v0. What is the change in velocity of the car if the man runs to the left so that his speed relative to the car is vrel just before he jumps off at the left end?
b. If there are n men each of mass m on the car, should they all run and jump off together or should they run and jump one by one in order to give a greater velocity to the car?

View Solution
