A body of mass 40 kg stands on a weighing machine in an accelerated lift. The reading on the scale of the weighing machine is 300 N. Find the magnitude and direction of acceleration. (g=9.8ms−2)
2.3 m/s2 upward
2.3 m/s2 downward
4.6 ms/2 upward
4.6 ms/2 downward
The correct Answer is:B
To solve the problem, we need to analyze the forces acting on the body when it is in an accelerated lift. Here’s a step-by-step breakdown:
Step 1: Identify the Forces
When the body is in the lift, two main forces act on it:
1. The gravitational force (weight) acting downwards, which is given by:
W=m⋅g
where m=40kg and g=9.8m/s2.
2. The normal force (N) exerted by the weighing machine, which is the reading on the scale.
Step 2: Calculate the Weight of the Body
Using the formula for weight:
W=40kg⋅9.8m/s2=392N
Step 3: Analyze the Situation in the Lift
Since the reading on the scale is 300 N, we can set up the equation based on Newton's second law. If the lift is accelerating downwards, the normal force will be less than the weight:
N=W−Fnet
where Fnet=m⋅a (the net force due to the acceleration of the lift).
Step 4: Set Up the Equation
From the above, we can write:
N=m⋅g−m⋅a
Substituting the known values:
300N=392N−40kg⋅a
Step 5: Solve for Acceleration
Rearranging the equation to solve for a:
40kg⋅a=392N−300N
40kg⋅a=92N
a=92N40kg=2.3m/s2
Step 6: Determine the Direction of Acceleration
Since the normal force (300 N) is less than the weight (392 N), the lift is accelerating downwards. Therefore, the direction of acceleration is downward.
Final Answer
The magnitude of acceleration is 2.3m/s2 and it is directed downwards.
---
When the body is in the lift, two main forces act on it:
1. The gravitational force (weight) acting downwards, which is given by:
W=m⋅g
where m=40kg and g=9.8m/s2.
Using the formula for weight:
W=40kg⋅9.8m/s2=392N
Since the reading on the scale is 300 N, we can set up the equation based on Newton's second law. If the lift is accelerating downwards, the normal force will be less than the weight:
N=W−Fnet
where Fnet=m⋅a (the net force due to the acceleration of the lift).
From the above, we can write:
N=m⋅g−m⋅a
Substituting the known values:
300N=392N−40kg⋅a
Rearranging the equation to solve for a:
40kg⋅a=392N−300N
40kg⋅a=92N
a=92N40kg=2.3m/s2
Since the normal force (300 N) is less than the weight (392 N), the lift is accelerating downwards. Therefore, the direction of acceleration is downward.
The magnitude of acceleration is 2.3m/s2 and it is directed downwards.
Similar Questions
A block of mass m kg is kept on a weighing machine in an elevator. If the elevator is retarding upward by a ms−2, the reading of weighing machine is
View SolutionA helicopter of mass 2000 kg rises with a vertical acceleration of 15ms−2. The total mass of the crew and passengers is 500 kg. Give the magnitude and direction of the (g=10ms−2)
(a) Force on the floor of the helicopter by the crew and passengers.
(b) action of the rotor of the helicopter on the surrounding air.
(c ) force on the helicopter dur to the surrounding air.
View Solution
Knowledge Check
A helicopter of mass 2000 kg rises with a vertical acceleration of 15ms−2. The total mass of the crew and passengers is 500 kg. Give the magnitude and direction of the (g=10ms−2)
(a) Force on the floor of the helicopter by the crew and passengers.
(b) action of the rotor of the helicopter on the surrounding air.
(c ) force on the helicopter dur to the surrounding air.AI and iiBii and iiiCI and iiiDAll the three
A man of mass 70 kg stands on a weighing scale in a lift which is moving downward with the uniform acceleration of 5ms2 . The reading on the weighing scale is
View SolutionA body of mass 50 kg is hung by a spring balance in a lift. Calculate the reading of the balance when :
The lift is ascending with an acceleration of 2m/s2.
View SolutionA boy of mass 40 kg climbs up a rope with an acceleration of 2ms−2 . What is the tension in the rope ?
View SolutionA block of mass m is placed on weighing machine and it is also attached with a spring balance. The whole system is placed in a lift as shown in figure. Left is moving with constant acceleration 10m/s2 in upward direction. The reading of the weighing machine is 500 N and the reading of spring balance is 300 N. Find the actual mass of the block in kg. (Takr g=10m/s2)

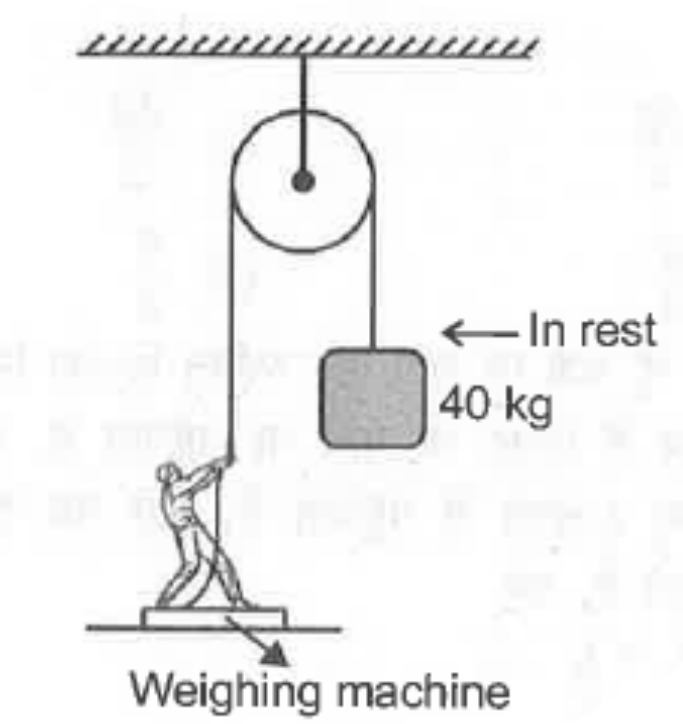
View SolutionA 80 kg man is standing on a weightless weighing machine as shown in the figure if mass of hanging block is 40 kg, then reading of weighing machine, is
View SolutionA man stands on a weighing machine kept inside a lift. Initially the lift is ascending with the acceleration 'a' due to which the reading is W. Now the lift decends with the same acceleration and reading 10% of initial. Find the acceleration of lift ?
View SolutionA man of mass 40kg is standing on a weighting machine kept on the floor of an elevator which is moving up with an acceleration of 2m/s2 Find the reading of the weighing maching.

View Solution
