An 8 kg block of ice, released from rest at the top of a 1.5 m long smooth ramp, slides down and falls with a velocity 2.5ms−1. Find angle of the ramp with horizontal.
(a)12∘
(b)18∘
(c)15∘
(d)30∘
The correct Answer is:1
To solve the problem step by step, we will follow the principles of kinematics and dynamics.
Step 1: Understand the Problem
We have an 8 kg block of ice that slides down a smooth ramp of length 1.5 m and reaches a velocity of 2.5 m/s at the bottom. We need to find the angle of the ramp with the horizontal.
Step 2: Use the Kinematic Equation
We can use the kinematic equation that relates initial velocity (u), final velocity (v), acceleration (a), and distance (s):
v2=u2+2as
Given:
- Initial velocity, u=0 (released from rest)
- Final velocity, v=2.5m/s
- Distance, s=1.5m
Substituting the values into the equation:
(2.5)2=0+2a(1.5)
6.25=3a
Step 3: Solve for Acceleration (a)
Now, we can solve for acceleration a:
a=6.253
a≈2.0833m/s2
Step 4: Relate Acceleration to the Angle of the Ramp
On the ramp, the component of gravitational force causing the acceleration down the ramp is given by:
ma=mgsinθ
Where:
- m is the mass of the block (which cancels out),
- g is the acceleration due to gravity (approximately 9.8m/s2).
From the equation:
a=gsinθ
Substituting the values:
2.0833=9.8sinθ
Step 5: Solve for sinθ
Rearranging gives:
sinθ=2.08339.8
sinθ≈0.2124
Step 6: Find the Angle θ
To find the angle θ, we take the inverse sine:
θ=sin−1(0.2124)
Calculating this gives:
θ≈12.2∘
Conclusion
Thus, the angle of the ramp with the horizontal is approximately 12∘.
We have an 8 kg block of ice that slides down a smooth ramp of length 1.5 m and reaches a velocity of 2.5 m/s at the bottom. We need to find the angle of the ramp with the horizontal.
We can use the kinematic equation that relates initial velocity (u), final velocity (v), acceleration (a), and distance (s):
v2=u2+2as
Given:
- Initial velocity, u=0 (released from rest)
- Final velocity, v=2.5m/s
- Distance, s=1.5m
(2.5)2=0+2a(1.5)
6.25=3a
Now, we can solve for acceleration a:
a=6.253
a≈2.0833m/s2
On the ramp, the component of gravitational force causing the acceleration down the ramp is given by:
ma=mgsinθ
Where:
- m is the mass of the block (which cancels out),
- g is the acceleration due to gravity (approximately 9.8m/s2).
a=gsinθ
Substituting the values:
2.0833=9.8sinθ
Rearranging gives:
sinθ=2.08339.8
sinθ≈0.2124
To find the angle θ, we take the inverse sine:
θ=sin−1(0.2124)
Calculating this gives:
θ≈12.2∘
Thus, the angle of the ramp with the horizontal is approximately 12∘.
Topper's Solved these Questions
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - ENABLE
50 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)
14 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
Similar Questions
A wedge of height 'h' is released from rest with a light particle P placed on it as shown. The wedge slides down an incline which makes an angle theta with the horizontal. All the surface are smooth, P will reach the surface of the incline in time:

View SolutionA wedge of height 'h' is released from rest with a light particle P placed on it as shown. The wedge slides down an incline which makes an angle theta with the horizontal. All the surface are smooth, P will reach the surface of the incline in time:

View Solution
Knowledge Check
A block released from rest from the top of a smooth inclined plane of angle θ1 reaches the bottom in time t1. The same block released from rest from the top of another smooth inclined plane of angle θ2 reaches the bottom in time t2 If the two inclined planes have the same height, the relation between t1andt2 is
At2t1=(sinθ1sinθ2)1/2Bt2t1=1Ct2t1=sinθ1sinθ2Dt2t1=sin2θ1sin2θ2
A block of ice starts sliding down from the top of an inclined roof of a along a line of the greatest slope. The inclination of the roof with the horizontal is 30∘. The heights of the highest and lowerst points of the roof are 8.1 m and 5.6 m respectively.At what horizontal distance from the lowest point will the block hit the ground ? Neglect air friction .[g=9.8m/s2].
View SolutionA block of mass 8 kg is released from the top of an inclined smooth surface as shown in figure. If spring constant of spring is 200 Nm^(-1) and block comes to rest after compressing spring by 1 m then find the distance travelled by block before it comes to rest

View SolutionA block of mass 8 kg is released from the top of an inclined smooth surface as shown in figure. If spring constant of spring is 200 Nm^(-1) and block comes to rest after compressing spring by 1 m then find the distance travelled by block before it comes to rest

View SolutionA sliding fit cylindrical body of mass of 1kg drops vertically down at a constant velocity of 5cms−1. Find the viscosity of the oil.

View SolutionA block A of mass m is held at rest on a smooth horizontal floor. A light frictionless, small pulley is fixed at a height of 6m from the floor. A light inextensible string of length 16m, connected with A passes over the pulley and another identical block B is hung from the string. Initial height of B is 5m from the floor as shown in figure
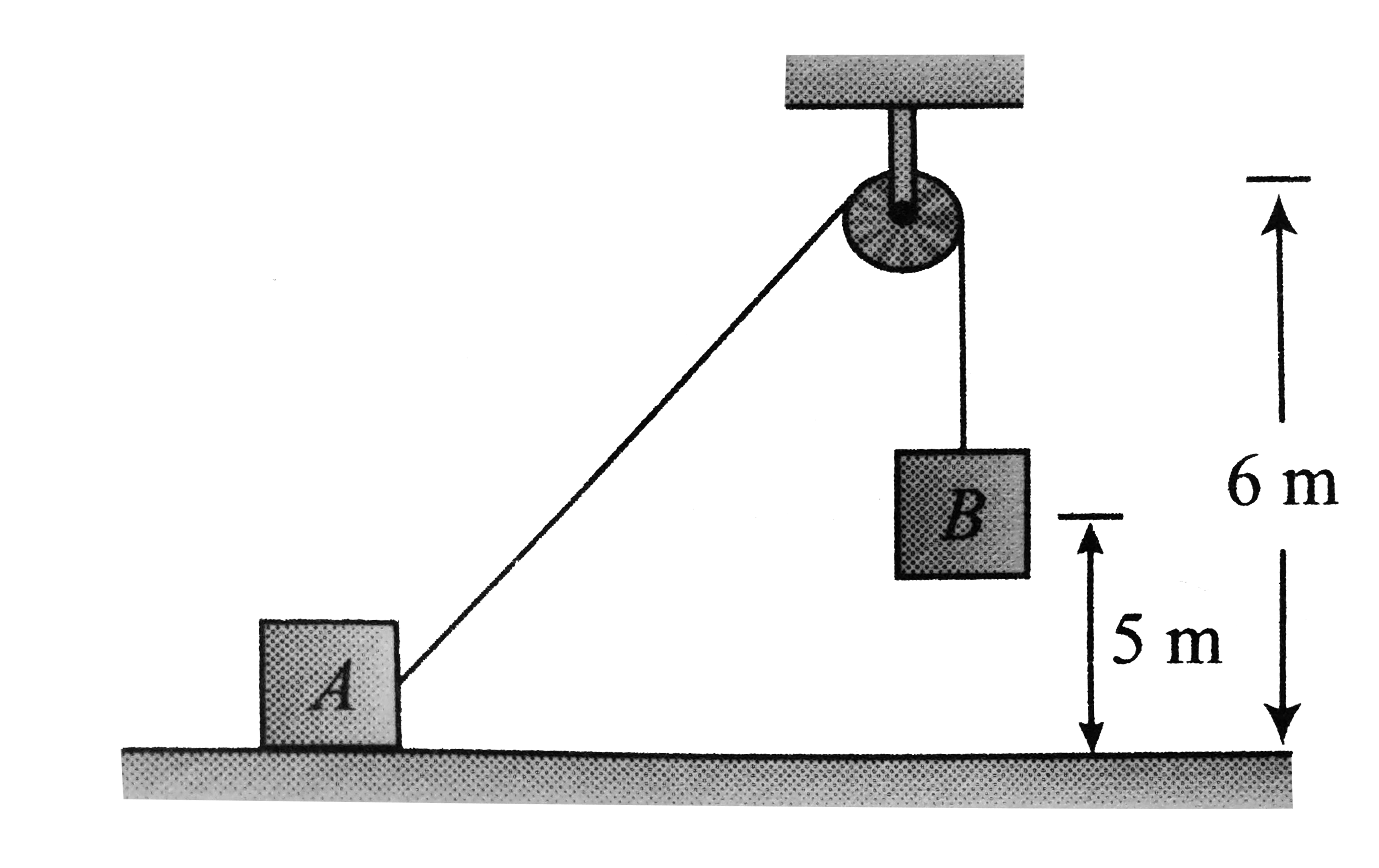
When the system is released from rest, B starts to move vertically downwards and A slides on the floor towards right.
a. If at an instant string makes an angle θ with horizontal, calculate relation between velocity u of A and v of B.
b. Calculate v when B strikes the floor. (g=10ms−2).
View SolutionA bullet is projected upwards from the top of a tower of height 90 m with the velocity 30ms−1 making an angle 30∘ with the horizontal. Find the time taken by it to reach the ground is (g=10ms−2)
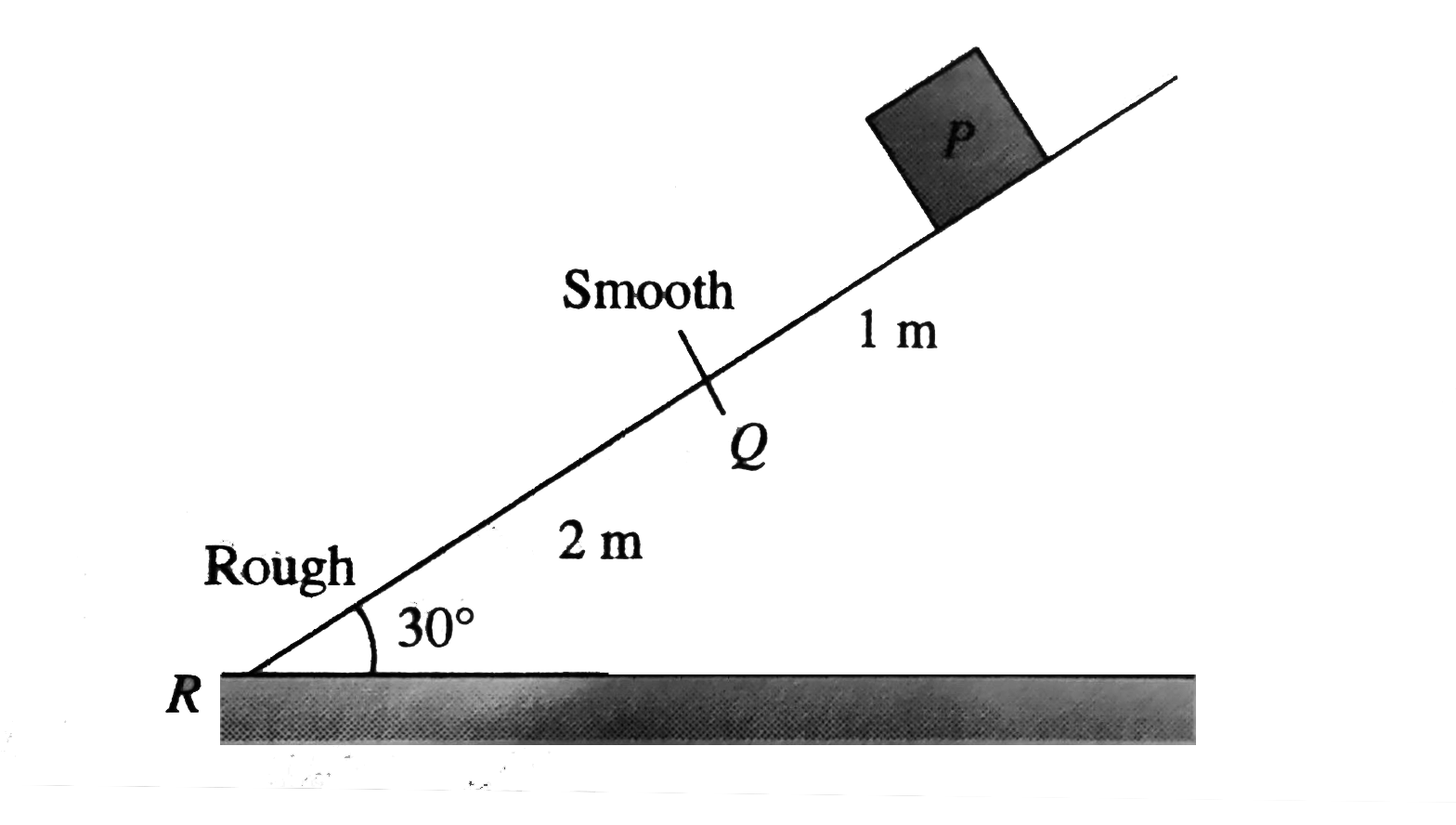
View SolutionA block of mass 5.0kg slides down from the top of an inclined plane of length 3m. The first 1m of the plane is smooth and the next 2m is rough. The block is released from rest and again comes to rest at the bottom of the plane. If the plane is inclined at 30∘ with the horizontal, find the coefficient of friction on the rough portion.
View Solution