A ball after falling a distance of 5 meter rest hits elastically the floor of a lift and rebounds. At the time of impact the lift was moving up with a velocity of 1m/sec. The velocity with which the ball rebounds just after impact is : (g=10m/sec2)
10 m/sec
11m/sec
12m/sec
13m/sec
The correct Answer is:C
To solve the problem step by step, we will follow these calculations:
Step 1: Calculate the velocity of the ball just before impact.
The ball falls from rest under the influence of gravity. We can use the equation of motion to find the velocity just before it hits the floor:
v=√2gh
Where:
- g=10m/s2 (acceleration due to gravity)
- h=5m (height from which the ball falls)
Substituting the values:
v=√2×10×5=√100=10m/s
Step 2: Identify the velocities at the time of impact.
At the time of impact:
- The velocity of the ball vB=10m/s (downward)
- The velocity of the lift vL=1m/s (upward)
Step 3: Use the principle of conservation of momentum for elastic collision.
In an elastic collision, the velocity of the ball after the collision can be calculated using the formula:
v′=vB+2vL
Where:
- v′ is the velocity of the ball after the impact.
- vB is the velocity of the ball just before impact.
- vL is the velocity of the lift.
Step 4: Substitute the values into the formula.
Now substituting the values we have:
v′=10m/s+2×1m/s
v′=10m/s+2m/s=12m/s
Conclusion:
The velocity with which the ball rebounds just after impact is 12m/s.
---
The ball falls from rest under the influence of gravity. We can use the equation of motion to find the velocity just before it hits the floor:
- g=10m/s2 (acceleration due to gravity)
- h=5m (height from which the ball falls)
At the time of impact:
- The velocity of the ball vB=10m/s (downward)
- The velocity of the lift vL=1m/s (upward)
In an elastic collision, the velocity of the ball after the collision can be calculated using the formula:
- v′ is the velocity of the ball after the impact.
- vB is the velocity of the ball just before impact.
- vL is the velocity of the lift.
Now substituting the values we have:
v′=10m/s+2m/s=12m/s
The velocity with which the ball rebounds just after impact is 12m/s.
Topper's Solved these Questions
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - EFFICIENT
50 Videos
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - IMPECCABLE
54 Videos
- WORK ENERGY AND POWER BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - IMPECCABLE
54 Videos
- WAVE MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (TRUE FALSE TYPE)
4 Videos
Similar Questions
A ball falls from a height such that it strikes the floor of lift at 10 m/s. If lift is moving in the upward direction with a velocity 1 m/s, then velocity with which the ball rebounds after elastic collision will be
View SolutionA coin is released inside a lift at a height of 2m from the floor of the lift. The height of the lift is 10 m. The lift is moving with an acceleration of 9m/s2downwards. The time after which the coin will strike with the lift is : (g=10m/s2)
View Solution
Knowledge Check
A body of mass m, moving with velocity μ collides elasticity with another body at rest having mass M. If the body of mass M moves with velocity V, then the velocity of the body of mass m after the impact is
Am−Mm+MμBm−Mm+MVCm+MVm+MDmu−MVm
A ball of mass 0.2 kg moves with a velocity of 20m/sec and it stops in 0.1 sec , then the force on the ball is
View SolutionA ball of mass 0.2 kg moves with a velocity of 20m/sec and it stops in 0.1 sec , then the force on the ball is
View SolutionA ball is dropped from a height of 20m and rebounds with a velocity which is 34 of the velocity with which it hits the ground. What is the time interval between the first and second bunces (g=10m/s2)
View SolutionA small ball falling vertically downward with constant velocity 4m/s strikes elastically a massive inclined cart moving with velocity 4m/s horizontally as shown. The velocity of the rebound of the ball is
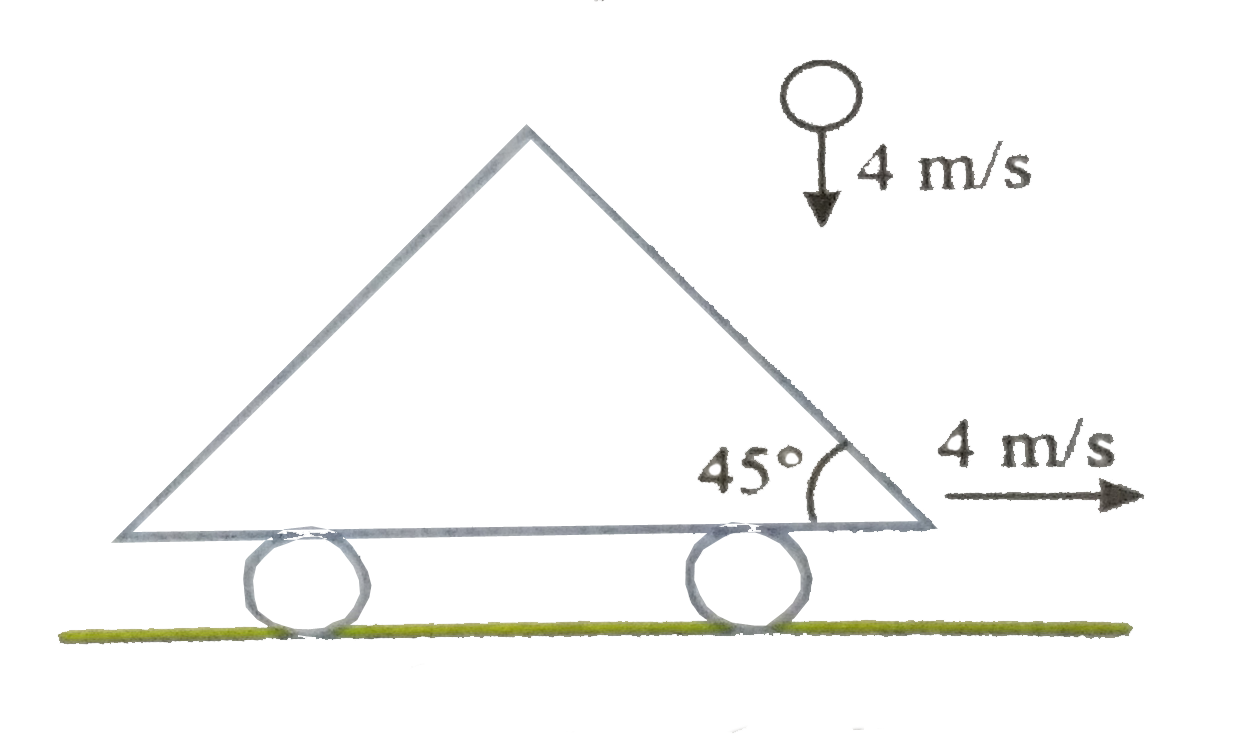
View SolutionA tennis ball is dropped on the floor from a height of 20m. It rebounds to a height of 5m. If the ball was in contact with the floor for 0.01s. What was its average acceleration during contact? (g=10m/s2)
View SolutionA ball moving with a velocity v hits a massive wall moving towards the ball with a velocity a. An elastic impact lasts for time △t
View SolutionA body is thrown up in a lift with a velocity 5ms−1 relative to the lift and the time of flight is found to be 0.8 s. The acceleration with which the lift is moving up is (g=10ms−2)
View Solution
