A fan of moment of inertia 0.6 kg × metre2 is to run upto a working speed of 0.5 revolution per second. Indicate the correct value of the angular momentum of the fan
0.6πkg×metre2sec
6πkg×metre2sec
3πkg×metre2sec
π6kg×metre2sec
The correct Answer is:A
To find the angular momentum of the fan, we can use the formula for angular momentum (L):
L=I⋅ω
where:
- L is the angular momentum,
- I is the moment of inertia,
- ω is the angular speed in radians per second.
Step 1: Identify the moment of inertia (I)
The moment of inertia of the fan is given as:
I=0.6kg⋅m2
Step 2: Convert the angular speed (ω) from revolutions per second to radians per second
The angular speed is given as:
Angular speed=0.5revolutions per second
To convert revolutions per second to radians per second, we use the fact that one revolution is equal to 2π radians:
ω=0.5revolutions/second×2πradians/revolution=πradians/second
Step 3: Calculate the angular momentum (L)
Now we can substitute the values of I and ω into the angular momentum formula:
L=I⋅ω=0.6kg⋅m2⋅πradians/second
Calculating this gives:
L=0.6πkg⋅m2/s
Step 4: Final Result
The angular momentum of the fan is:
L≈1.884kg⋅m2/s(using π≈3.14)
Thus, the correct value of the angular momentum of the fan is approximately 1.884kg⋅m2/s.
- L is the angular momentum,
- I is the moment of inertia,
- ω is the angular speed in radians per second.
The moment of inertia of the fan is given as:
The angular speed is given as:
Now we can substitute the values of I and ω into the angular momentum formula:
The angular momentum of the fan is:
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EFFICIENT
50 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE
56 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE
56 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B
10 Videos
Similar Questions
A fan of moment of inertia 0.6kgm2 is moving with a speed of 0.5 r.p.s. The angular momentum of the fan is
View SolutionA flywheel of moment of inertia 5.0 kg m^2 is rotated at a speed of 60 rad/s. Because of the friction at the axle, it comes to rest in 5.0 minutes. Find a. The average torque of the friction. B. the total work done by the friction and c. the angular momentum of the wheel 1 minute before it stops rotating.
View SolutionIf a body of moment of inertia 2kgm2 revolves about its own axis making 2 rotations per second, then its angular momentum (in J s) is
View SolutionA wheel of moment of inertia 0.10kg−m2 is rotating about a shaft at an angular speed of 160revmin. A second wheel is set into rotation at 300 rev/minute and is coupled to the same shaft so that both the wheels finally rotate with as common angular speed of 200 rev/minute. Find the moment of inertia of the second wheel.
View SolutionA ring of mass 10kg and diameter 0.4m is rotated about an axis passing through its centre. If it makes 1800 revolutions per minute then , the angular momentum of the ring is
View SolutionA flywheel of moment of inertia 5.0kg−m2 is rotated at a speed of 10rad/s because of the friction at the axis it comes to rest in 10s. Find the average torque of the friction.
View SolutionA small source of sound vibrating at frequency 500 Hz is rotated in a circle of radius 1002π cm at a constant angular speed of 5-0 revolutions per second. A listener situates himself in the plane of the circle. Find the minimum and the maximum frequency of the sound observed. Speed of sound in air =332ms−1.
View Solution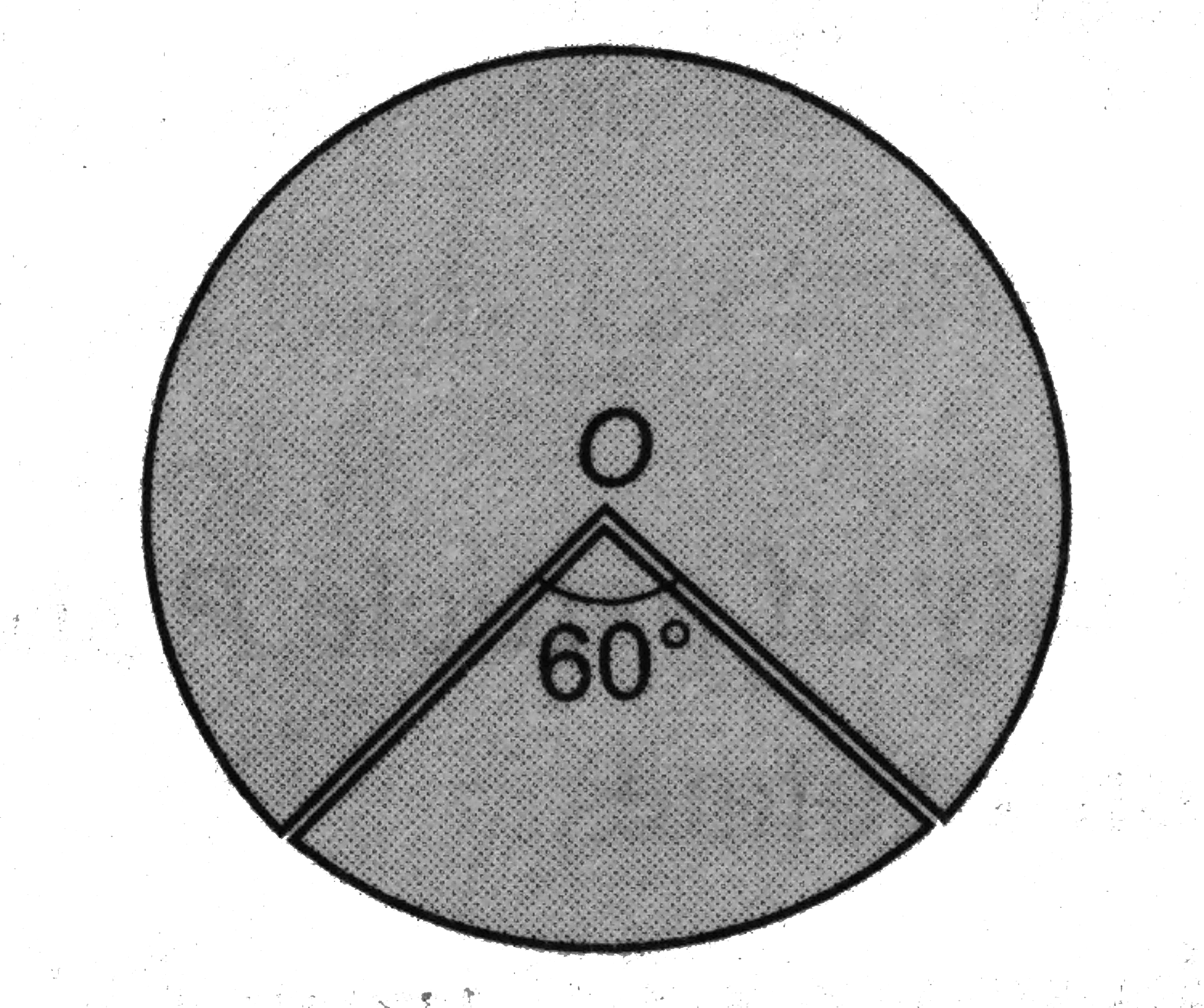
The uniform disc shown in the figure has a moment of inertia of 0.6kg−m2 around the axis that passes through O and is perpendicular to the plane of the page. If a segment is cut out from the disc as shown, what is the moment of inertia of the remaining disc?
View SolutionA wheel of moment of inertia 30kgm2 is rotating at 10 rotations per minute. The work done in increasing its speed to 5 times its initial value will be
View SolutionA wheel of mass 8 kg has moment of inertia equals to 0.5kg-m2. Determine its radius of gyration.
View Solution
