The acceleration of any electron due to the magnetic fields is
3.14×1014m/s2
4.28×1014m/s2
5.56×1012m/s2
6.28×1014m/s2
The correct Answer is:D
To find the acceleration of an electron due to a magnetic field, we can follow these steps:
Step 1: Understand the Force on a Charged Particle in a Magnetic Field
The force experienced by a charged particle (like an electron) moving in a magnetic field is given by the Lorentz force equation:
F=q(v×B)
where:
- F is the magnetic force,
- q is the charge of the particle,
- v is the velocity vector of the particle,
- B is the magnetic field vector.
Step 2: Analyze Different Cases of Electron Projection
1. Parallel to the Magnetic Field: If the electron is projected parallel to the magnetic field, the angle θ between v and B is 0 degrees. Thus:
F=qvBsin(0)=0
Therefore, the acceleration a is also 0.
2. Perpendicular to the Magnetic Field: If the electron is projected perpendicular to the magnetic field, the angle θ is 90 degrees. Thus:
F=qvBsin(90)=qvB
This force causes the electron to move in a circular path, and the centripetal force required for circular motion is provided by this magnetic force:
mv2r=qvB
Rearranging gives:
r=mvqB
3. At an Angle θ: If the electron is projected at an angle θ to the magnetic field, the force can be split into two components: one parallel and one perpendicular to the magnetic field. The parallel component does not contribute to acceleration, while the perpendicular component does.
Step 3: Calculate the Acceleration
The acceleration a due to the magnetic force can be expressed as:
a=Fm=qvBm
Step 4: Substitute Known Values
Using the known values:
- Charge of an electron, q=1.6×10−19C
- Mass of an electron, m=9.1×10−31kg
- Assuming a constant velocity v and magnetic field B, we can express acceleration as:
a=qBvm
Step 5: Example Calculation
Assuming v/B is a constant value, we can substitute values to find acceleration:
a=(1.6×10−19)(B)(v)9.1×10−31
Assuming vB=35.7×102:
a=(1.6×10−19)(35.7×102)9.1×10−31≈6.28×1014m/s2
Conclusion
The acceleration of the electron due to the magnetic field is approximately:
a≈6.28×1014m/s2
The force experienced by a charged particle (like an electron) moving in a magnetic field is given by the Lorentz force equation:
F=q(v×B)
where:
- F is the magnetic force,
- q is the charge of the particle,
- v is the velocity vector of the particle,
- B is the magnetic field vector.
1. Parallel to the Magnetic Field: If the electron is projected parallel to the magnetic field, the angle θ between v and B is 0 degrees. Thus:
F=qvBsin(0)=0
Therefore, the acceleration a is also 0.
F=qvBsin(90)=qvB
This force causes the electron to move in a circular path, and the centripetal force required for circular motion is provided by this magnetic force:
mv2r=qvB
Rearranging gives:
r=mvqB
The acceleration a due to the magnetic force can be expressed as:
a=Fm=qvBm
Using the known values:
- Charge of an electron, q=1.6×10−19C
- Mass of an electron, m=9.1×10−31kg
- Assuming a constant velocity v and magnetic field B, we can express acceleration as:
a=qBvm
Assuming v/B is a constant value, we can substitute values to find acceleration:
a=(1.6×10−19)(B)(v)9.1×10−31
Assuming vB=35.7×102:
a=(1.6×10−19)(35.7×102)9.1×10−31≈6.28×1014m/s2
The acceleration of the electron due to the magnetic field is approximately:
a≈6.28×1014m/s2
Topper's Solved these Questions
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - Illustration
55 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - SOLVED EXAMPLES
20 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - EFFICIENT
50 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
1 Videos
Similar Questions
An electron files into a homogeneous magnetic field of 10−3 perpendicular to the force lines. The velocity of the electron is v=4×107ms−1 what is the tangential acceleration of electron in the magnetic field ?
View SolutionThe factor(s) affecting the curvature of the trajectory of an electron moving in a magnetic field is -
View SolutionThe acceleration of electron due to mutual attraction between electron and a proton when they are 1.6 Angstroms apart is
View SolutionA: The electric field induced due to changing magnetic field is non-conservative,
R: The line integral of the electric field induced due to changing magnetic field along a closed loop is always zero.
View SolutionIn the given figure, the electron enters into the magnetic field. It deflects in ...... .. direction .
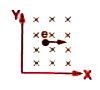
View SolutionWhen an electron is accelerated through a potential difference V, it experience a force F through as uniform transverse magnetic field. If the potential difference is increased to 2V, the force experoenced by the electron in the same magnetic field is
View SolutionCalculate the change in magnetic dipole moment when the electron in a H−atom makes a transition from the n=4 orbit to the n=3 orbit. Suppose that the atoms is in a magnetic field of induction. Calculate the change in energy when it makes the same transition and the corresponding change in frequency of the emitted photon due to the magnetic field.
View Solution(A) : If an electron is not deflected while passing through a certain region of space, then only possibility is that there is no magnetic field in this region
(R) : Force on an electron moving in a magnetic field is inversely proportional to the magnetic field applied.
View SolutionAn electron is orbiting is a circular orbit of radius r under the influence of a constant magnetic field of strength B. Assuming that Bohr postulate regarding the quantisation of angular momentum holds good for this elerctron, find
(a) the allowed values of te radius r of the orbit.
(b) the kinetic energy of the electron in orbit
(c ) the potential energy of insteraction between the magnetic moment of the orbital current due to the electron moving in its orbit and the magnetic field B.
(d) the total energy of the allowed energy levels.
(e) the total magnetic flux due to the magnetic field B passing through the nth orbit. (Assume that the charge on the electronis -e and the mass of the electron is m).
View SolutionThe cyclotron frequency of an electron gyrating in a magnetic field of 1T is approximately:
View Solution
