A series AC circuit consists of an inductor and a capacitor. The inductance and capacitance is respectively 1henry and 25μF if the current is maximum in circuit then angular frequency will be
200
100
50
200/2
The correct Answer is:A
To solve the problem, we need to find the angular frequency (ω) at which the current in a series AC circuit consisting of an inductor and a capacitor is at its maximum. This occurs when the inductive reactance (XL) equals the capacitive reactance (XC), which is the condition for resonance.
1. Identify Given Values:
- Inductance (L) = 1 Henry
- Capacitance (C) = 25 microfarads = 25 × 10^(-6) F
2. Understand the Condition for Maximum Current:
- For maximum current in the circuit, the inductive reactance (XL) must equal the capacitive reactance (XC):
XL=XC
3. Express Reactances in Terms of Angular Frequency:
- The inductive reactance is given by:
XL=ωL
- The capacitive reactance is given by:
XC=1ωC
4. Set the Reactances Equal:
- Setting the two expressions equal gives:
ωL=1ωC
5. Rearranging the Equation:
- Multiply both sides by ωC:
ω2LC=1
- Rearranging gives:
ω2=1LC
6. Substituting the Values:
- Substitute L = 1 H and C = 25 × 10^(-6) F into the equation:
ω2=11×25×10−6=125×10−6=10625
7. Calculating ω:
- Taking the square root of both sides:
ω=√10625=10005=200 rad/s
Final Answer:
The angular frequency (ω) at which the current is maximum in the circuit is 200 rad/s.
---
- Inductance (L) = 1 Henry
- Capacitance (C) = 25 microfarads = 25 × 10^(-6) F
- For maximum current in the circuit, the inductive reactance (XL) must equal the capacitive reactance (XC):
XL=XC
- The inductive reactance is given by:
XL=ωL
- The capacitive reactance is given by:
XC=1ωC
- Setting the two expressions equal gives:
ωL=1ωC
- Multiply both sides by ωC:
ω2LC=1
- Rearranging gives:
ω2=1LC
- Substitute L = 1 H and C = 25 × 10^(-6) F into the equation:
ω2=11×25×10−6=125×10−6=10625
- Taking the square root of both sides:
ω=√10625=10005=200 rad/s
The angular frequency (ω) at which the current is maximum in the circuit is 200 rad/s.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - ENABLE
50 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - EFFICIENT
49 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G
10 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)
89 Videos
Similar Questions
An AC circuit consists of an inductor of inductance 0.5H and a capacitor of capacitance 8μF in series. The current in the circuit is maximum when the angular frequency of AC source is
View SolutionIn a series AC circuit containing a capacitor and a resistor only
View SolutionAn oscillator circuit consists of an inductance of 0.5mH and a capacitor of 20μF. The resonant frequency of the circuit is nearly
View SolutionIn an AC circuit containing only capacitance the current
View SolutionAn L−C circuit consists of a 20.0mH inductor and a 0.5μF capacitor. If the maximum instantaneous current is 0.1A, what is the greatest potential difference across the capacitor?
View SolutionFor an LCR series circuit with an ac source of angular frequency ω.
View SolutionIn the circuit shown in figure, the charge stored on a capacitor of capacitance 3μF is
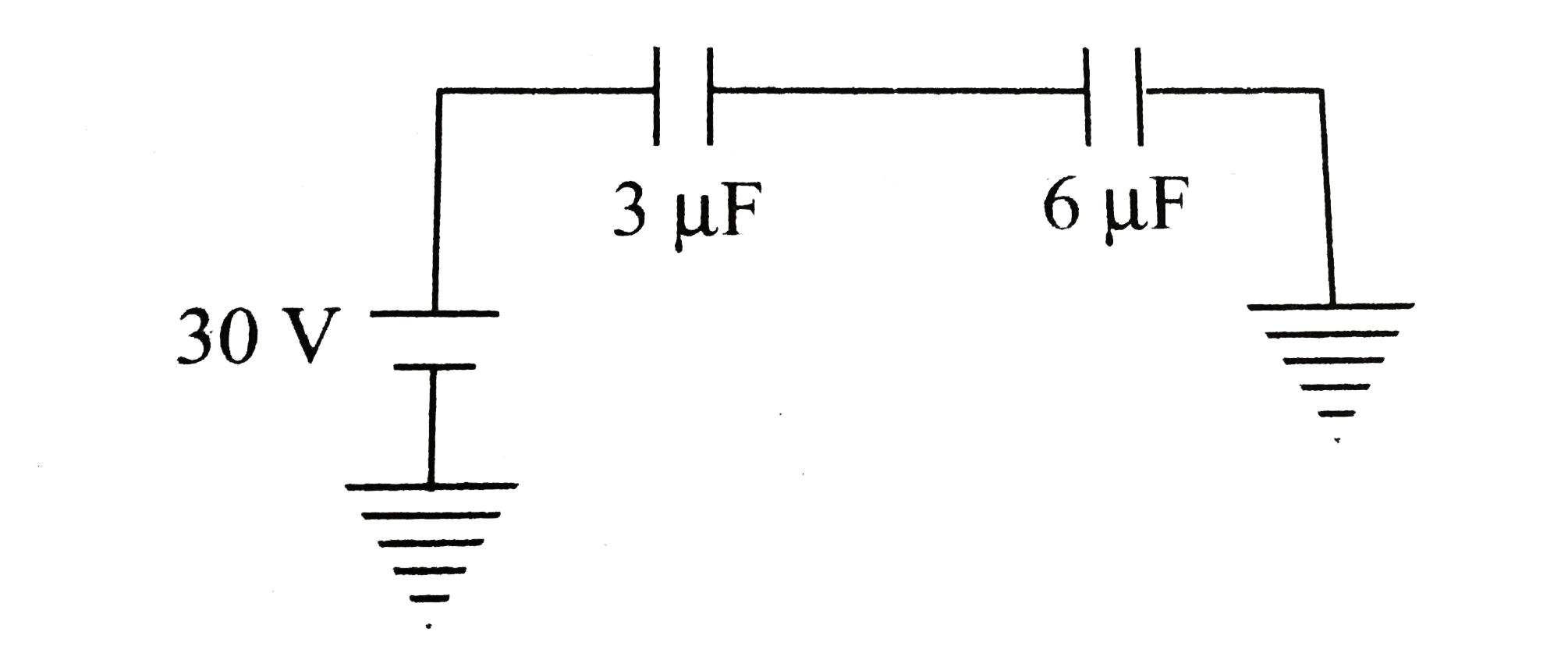
View SolutionA series AC circuit contains an inductor (20mH), a capacitor (100μF), a resistor (50Ω) and an AC source of 12V,50Hz. Find the energy dissipated in the circuit in 1000s.
View SolutionShows a part of a circuit. If all the capacitors have a capacitance of 2μF, then the
 .
.
View SolutionAn L−C circuit consists of an inductor with L=0.0900H and a capacitor of C=4x10−4F. The initial charge on the capacitor is 5.00μC, and the initial current in the inductor is zero.
(a) What is the maximum voltage across the capacitor?
(b) What is the maximum current in the inductor?
(c) What is the maximum energy stored in the inductor?
(d) When the current in the inductor has half its maximum value, what is the charge on the capacitor and what is the energy stored in the inductor?
View Solution
