A fish looking up through the water sees the outside world contained in a circular horizon. If the refractive index of water is 43 and the fish is 12 cm below the surface, the radius of this circle is cm is
36√7
36√7
36√5
4√5
The correct Answer is:B
Step by step video & image solution for A fish looking up through the water sees the outside world contained in a circular horizon. If the refractive index of water is (4)/(3) and the fish is 12 cm below the surface, the radius of this circle is cm is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS AND WAVE OPTICS EXERCISE - EFFICIENT49videos
RAY OPTICS AND WAVE OPTICS
- BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS AND WAVE OPTICS EXERCISE - IMPECCABLE58videos
RAY OPTICS AND WAVE OPTICS
- BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS AND WAVE OPTICS EXERCISE - IMPECCABLE58videos
RAY OPTICS AND WAVE OPTICS
- BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - IN-CHAPTER EXERCISE-J10videos
RAY OPTICS
- BOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-15 JEE - 2020EXERCISE - PHYSICS25videos
REVISION TEST-15 JEE - 2020
Similar Questions
A coin placed at the bottom of a beaker appears to be raised by 4.0 cm. If the refractive index of water is 4/3, find the depth of the water in the beaker.
View SolutionA fish in an aquarium approaches the left wall at a rate of 3ms−1 observes a fly approaching it at 8ms−1. If the refractive index of water is (4/3), find the actual velocity of the fly.
 View Solution
View SolutionA fish in an aquarium approaches the left wall at a rate of 3ms−1 observes a fly approaching it at 8ms−1. If the refractive index of water is (4/3), find the actual velocity of the fly.
 View Solution
View SolutionIn a pond of water, a flame is held 2 m above the surface of the water. A fish is at depth of 4 m from the water surface. Refractive index of water is 43. The apparent height of the flame from the eyes of fish is -
View SolutionAn object O is kept in air and a lens of focal length 10cm (in air) is kept at the botton of a container which is filled upto a height 44cm by water. The refractive index of water is 4/3 and that of glass is 3/2. The botton of the container is closed by a thin glass slab of refractive index 3/2. Find the distance (in cm) of the final image formed by the system from botton of container (refer to figure shown below).
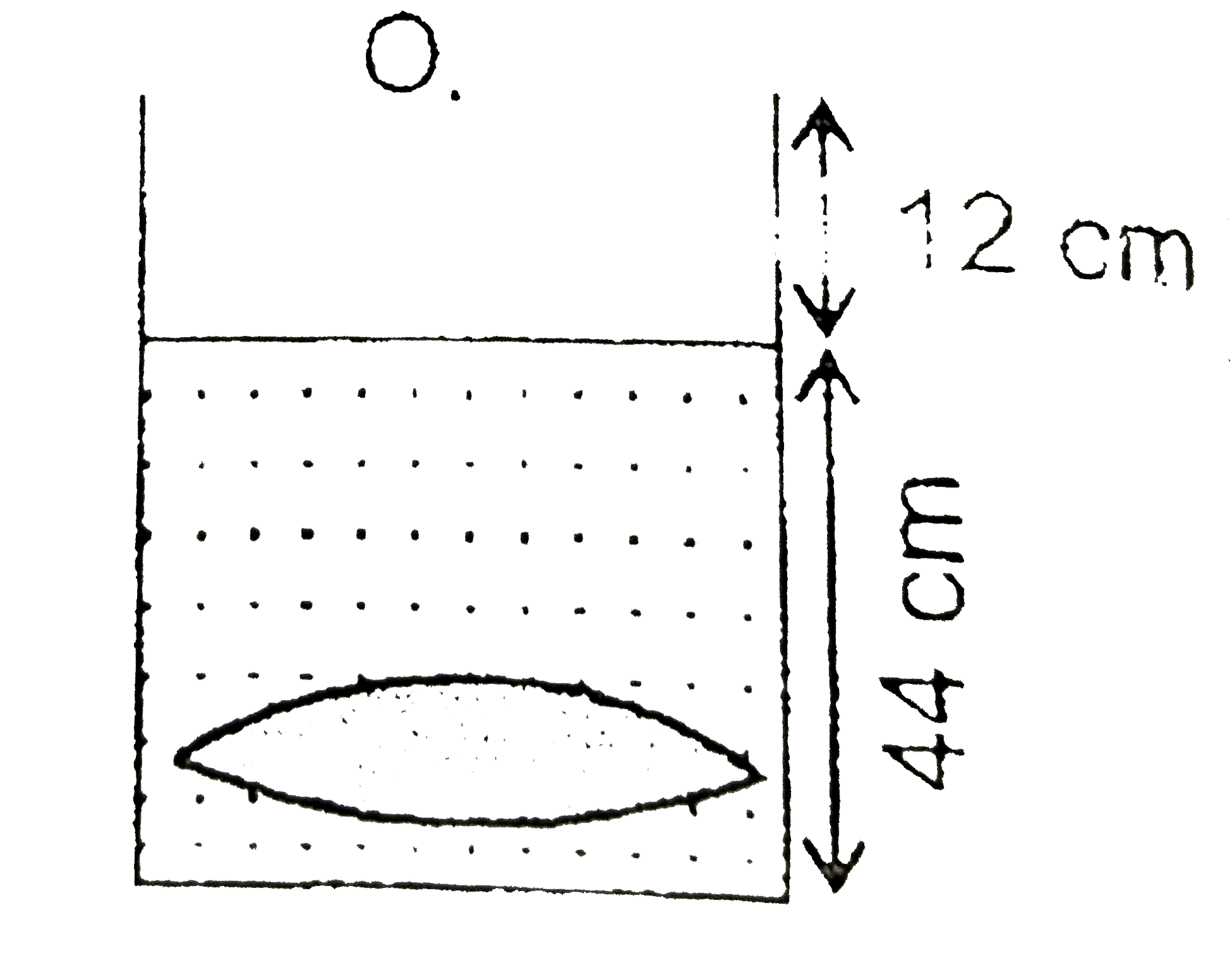 View Solution
View SolutionA fish rising vertically to the surface of water in a lake uniformly at the rate of 3ms−1 observes a bird diving vertically towards the water at a rate of 9ms−1 vertically above it. If the refractive index of water is 4/3 the actual velocity of the dive of the bird is (in ms−1)
View SolutionA ball is dropped from a height of 20m above the surface of water in a lake. The refractive index of water is 4/3. A fish inside the lake , in the line fall of the ball, is looking at the ball. At an instant when the balll is 12.8m above the water surface, the fish sees the speed of ball as .
View SolutionA fish lies at the bottom of a 4m deep water lake. A bird flies 6m above the water surface and refractive index of water is 4/3 . Then the distance between
View SolutionA fish looks upward at an unobstructed overcast sky. What total angle does the sky appear to subten?(Take refractive index of water as √2.)
View SolutionA container contains water up to a height of 20 cm and there is a point source at the centre of the bottom of the container. A rubber ring of radius r floats centrally on the water. The ceiling of the room is 2.0 m above the water surface. (a) Find the radius of the shadow of the ring formed on the ceiling if r = 15 cm. (b) Find the maximum value of r for which the shadow of the ring is formed on the ceiling. Refractive index of water =4/3.
View Solution
