Light of wavelength λ0 in air enters a medium of refractive index n. If two points A and B in this medium lie along the path of this light at a distance x, then phase difference ϕ0 between these two point is
ϕ0=1n2πλ0x
ϕ0=n2πλ0x
ϕ0=(n−1)(2πλ0)x
ϕ0=1n−12πλ0x
The correct Answer is:B
To find the phase difference ϕ0 between two points A and B in a medium with refractive index n, we can follow these steps:
1. Identify the Optical Path Difference (OPD):
The optical path difference between two points A and B in a medium is given by the formula:
OPD=n⋅x
where n is the refractive index of the medium and x is the distance between points A and B.
2. Relate Optical Path Difference to Phase Difference:
The phase difference ϕ0 can be related to the optical path difference using the formula:
ϕ0=2πλ⋅OPD
where λ is the wavelength of light in the medium.
3. Substitute the OPD into the Phase Difference Formula:
By substituting the expression for OPD into the phase difference formula, we get:
ϕ0=2πλ⋅(n⋅x)
4. Adjust for Wavelength in Air:
Since the wavelength of light in the medium is different from that in air, we can express the wavelength in the medium λ as:
λ=λ0n
where λ0 is the wavelength of light in air.
5. Final Expression for Phase Difference:
Substituting λ into the phase difference formula gives:
ϕ0=2πλ0n⋅(n⋅x)=2πnxλ0
Thus, the phase difference ϕ0 between points A and B is:
ϕ0=2πnxλ0
The optical path difference between two points A and B in a medium is given by the formula:
OPD=n⋅x
where n is the refractive index of the medium and x is the distance between points A and B.
The phase difference ϕ0 can be related to the optical path difference using the formula:
ϕ0=2πλ⋅OPD
where λ is the wavelength of light in the medium.
By substituting the expression for OPD into the phase difference formula, we get:
ϕ0=2πλ⋅(n⋅x)
Since the wavelength of light in the medium is different from that in air, we can express the wavelength in the medium λ as:
λ=λ0n
where λ0 is the wavelength of light in air.
Substituting λ into the phase difference formula gives:
ϕ0=2πλ0n⋅(n⋅x)=2πnxλ0
ϕ0=2πnxλ0
Topper's Solved these Questions
- RAY OPTICS AND WAVE OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS AND WAVE OPTICS EXERCISE - IMPECCABLE
58 Videos
- RAY OPTICS AND WAVE OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS AND WAVE OPTICS EXERCISE - ENABLE
50 Videos
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - IN-CHAPTER EXERCISE-J
10 Videos
- REVISION TEST-15 JEE - 2020BOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-15 JEE - 2020EXERCISE - PHYSICS
25 Videos
Similar Questions
Find the speed of light of wavelength λ=780nm (in air) in a medium of refractive index μ=1.55.
(b) What is the wavelength of this light in the given medium ?
View Solution(i) Find the speed of light of wavelength λ=780 nm (in air) in a medium of of refractive index µ=1.55.
(ii) What is the wave length of this light in the given medium?
View SolutionA monochromatic beam of light of wavelength 6000A in vacuum enters a medium of refractive index 1.5. In the medium its wavelength is…., its frequency is…..
View SolutionLight waves of wave length λ propagate in a medium. If M end N are two points on the wave front and they are separated by a distance λ/4, the phase difference between them will be (in radian)
View SolutionA ray of light of wavelength u0 and frequency v0 enters a glass slab of refractice index μ from air. Then
View SolutionIf the wavelength of light in vacuum be λ, the wavelength in a medium of refractive index n will be
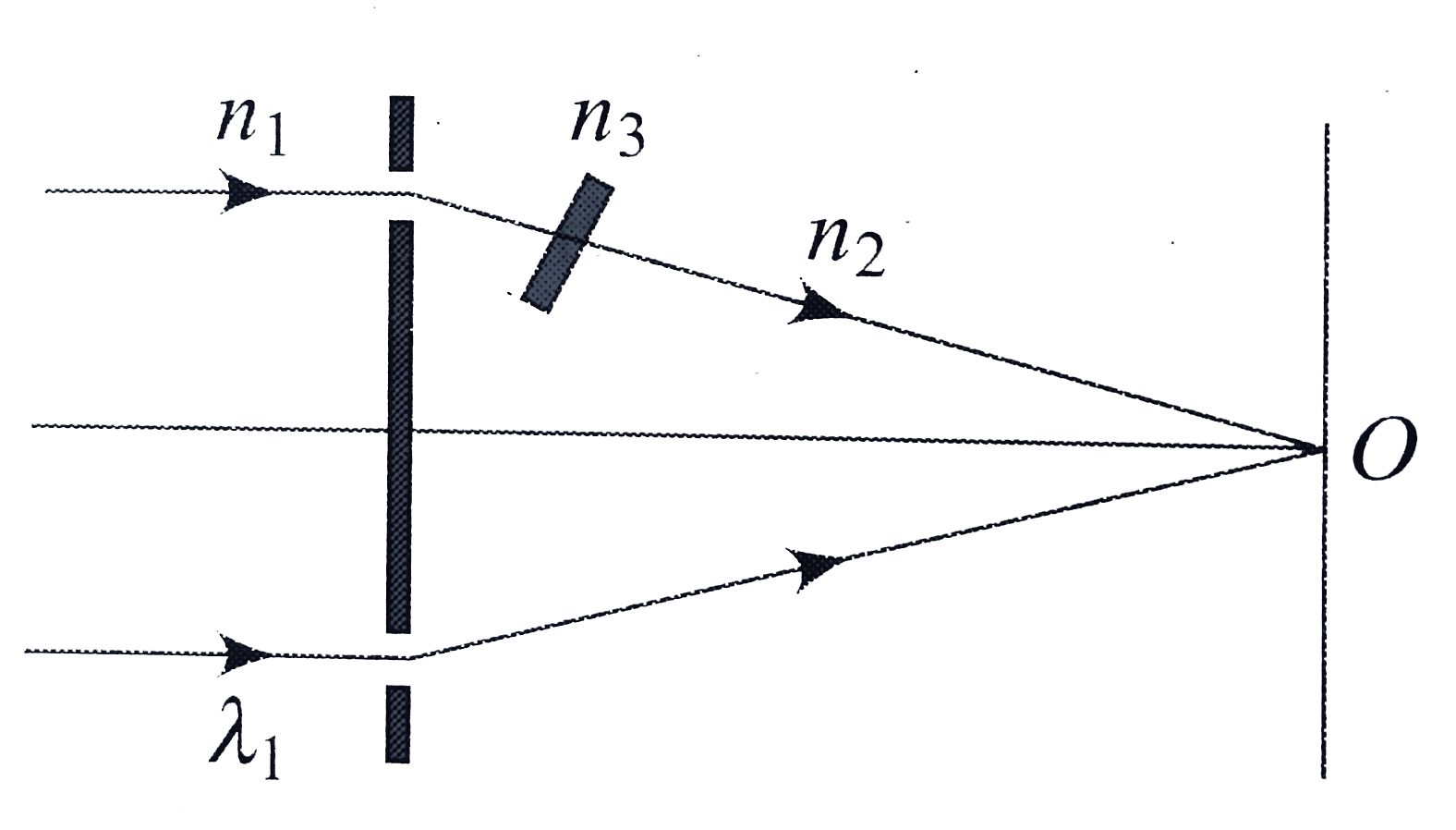
View SolutionIn YDSE shown in figure a parallel beam of light is incident on the slits from a medium of refractive index n1. The wavelength of light in this medium is λ1. A transparent slab of thickness t and refractive index n3 is put in front of one slit. The medium between the screen and the plane of the slits is n2. The phase difference between the light waves reaching point O (symmetrical, relative to the slits) is
View SolutionA light wave of frequency 5×1014Hz enters a medium of refractive index 1.5. In the velocity of the light wave is ….. And its wavelength is ……
View SolutionA monochromatic beam of light of wavelength λ and frequency v goes from vacum to a medium of refractive index n. How do the wavelength and frequency of light change ?
View SolutionTwo light waves having the same wavelength λ in vacuum are in phase initially. Then the first ray travels a path of length L1 through a medium of refractive index μ1. Then second ray travels a path of length L2 throug a medium of refractive index μ2. The two waves are then combined to observed interference effects. The phase difference between the two, when they interfere, is
View Solution
