Two closed vessel A and B of equal volume containing air at pressure P1 and temperature T1 are connected to each other through a naroow open tube. If th temperature of one is now maintained at T1 and other at T2 (wehre T1>T2 ) then that what will be the final pressure ?
T12P1T2
2P1P2T1+T2
2P1T1T1−T2
2P1T1+T2
To solve the problem, we will use the ideal gas law and the concept of conservation of moles. Here’s the step-by-step solution:
Step 1: Understand the Initial Conditions
We have two vessels A and B of equal volume containing air at pressure P1 and temperature T1. Vessel A is maintained at temperature T1 and vessel B is maintained at a lower temperature T2 (where T1>T2).
Step 2: Apply the Ideal Gas Law
The ideal gas law is given by the equation:
PV=nRT
Where:
- P = pressure
- V = volume
- n = number of moles
- R = universal gas constant
- T = temperature in Kelvin
Step 3: Calculate Initial Moles in Each Vessel
For vessel A:
nA=P1VRT1
For vessel B (initially at temperature T1):
nB=P1VRT1
Step 4: Set Up the Equation for Final Moles
Since the total number of moles before and after the connection remains constant, we can write:
nA+nB=nfinal
After the connection, the pressure in both vessels will equalize.
Step 5: Write the Final Pressure Equation
Let the final pressure be P. The number of moles in each vessel after the connection can be expressed as:
For vessel A (at T1):
nA=PVRT1
For vessel B (at T2):
nB=PVRT2
Step 6: Combine the Moles Equation
Equating the initial and final moles gives:
P1VRT1+P1VRT1=PVRT1+PVRT2
This simplifies to:
2P1=PT1+PT2
Step 7: Factor Out P
Factoring out P from the right side:
2P1=P(1T1+1T2)
Step 8: Solve for Final Pressure P
Rearranging the equation gives:
P=2P1T1T2T1+T2
Final Answer
Thus, the final pressure P in the system is:
P=2P1T2T1+T2
We have two vessels A and B of equal volume containing air at pressure P1 and temperature T1. Vessel A is maintained at temperature T1 and vessel B is maintained at a lower temperature T2 (where T1>T2).
The ideal gas law is given by the equation:
PV=nRT
Where:
- P = pressure
- V = volume
- n = number of moles
- R = universal gas constant
- T = temperature in Kelvin
For vessel A:
nA=P1VRT1
nB=P1VRT1
Since the total number of moles before and after the connection remains constant, we can write:
nA+nB=nfinal
After the connection, the pressure in both vessels will equalize.
Let the final pressure be P. The number of moles in each vessel after the connection can be expressed as:
For vessel A (at T1):
nA=PVRT1
nB=PVRT2
Equating the initial and final moles gives:
P1VRT1+P1VRT1=PVRT1+PVRT2
This simplifies to:
2P1=PT1+PT2
Factoring out P from the right side:
2P1=P(1T1+1T2)
Rearranging the equation gives:
P=2P1T1T2T1+T2
Thus, the final pressure P in the system is:
P=2P1T2T1+T2
Similar Questions
Two closed vessels of equal volume containing air at pressure P1 and temperature T1 are connected to each other through a narrow tube. If the temperature in one of the vessels is now maintained at T1 and that in the other at T2, what will be the pressure in the vessels?
View SolutionTwo closed vessels of equal volume containing air at pressure P1 and temperature T1 are connected to each other through a narrow tube. If the temperature in one of the vessels is now maintained at T1 and that in the other at T2, what will be the pressure in the vessels?
View SolutionTwo closed bulbs of equal volume (V) containing an ideal gas initially at pressure Pi and temperature T1 are connected through a narrow tube of negligible volume as shown in the figure below . The temperature of one of the bulbs is then raised to T2 . the final pressure Pf is
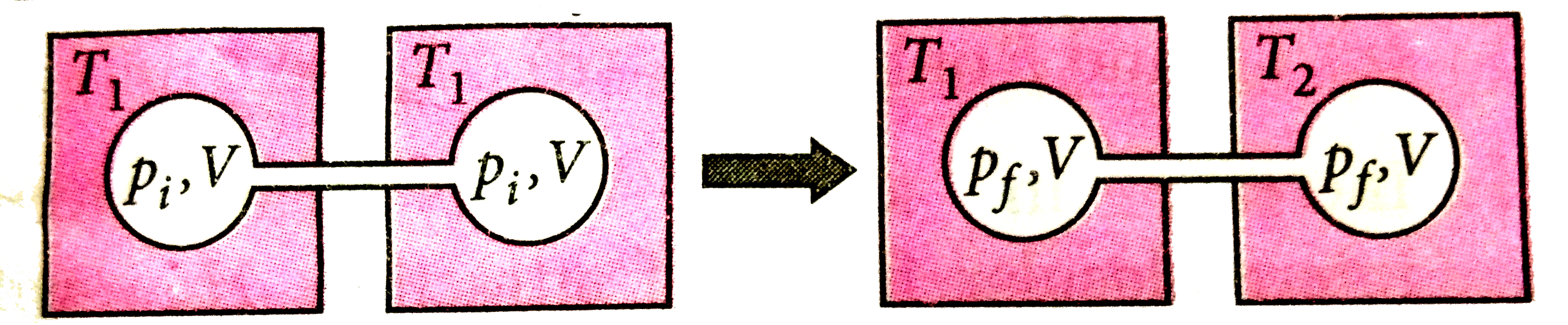
View SolutionA closed vessel A having volume V contains N2 at pressure P and temperature T. another closed vessel B having the same volume V contains. He at the same pressure P. but temperature 2T. The ratio of masses of N2 and He in the vesses A and B is
View SolutionGaseous system is placed with pressure P1, volume V1 and temperature T1, it has undergone thermodynamic changes where temperature is remaining constant, it is
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionTwo adiabatic containers have volumes V1 and V2 respectively. The first container has monoatomic gas at pressure p1 and temperature T1. The second container has another monoatomic gas at pressure p2 and temperature T2. When the two containers are connected by a narrow tube, the final temperature and pressure of the gases in the containers are P and T respectively. Then
View SolutionTwo cylienders fitted with pistons and placed as shown, connected with string through a small tube of negligible volume, are filled with gas at pressure P0 and temperature T0. The radius of smaller cylinder is half of the other. If the temperature is increased to 2T0, find the pressure if the piston of bigger cylinder moves towards left by 1 metre ?

View SolutionTwo idential container joined by a small pipe initially contain the same gas at pressure p0 and absolute temperature T0. One container is now maintained at the same temperature while the other is heated to 2T0. The common pressure of the gas
View Solution
