The available space occupied by spheres of equal size in three dimensions in both hcp and ccp arrangement is
0.74
0.7
0.604
0.524
The correct Answer is:A
To determine the available space occupied by spheres of equal size in three dimensions in both hexagonal close packing (hcp) and cubic close packing (ccp) arrangements, we will calculate the packing efficiency of these arrangements.
1. Understanding Packing Efficiency:
Packing efficiency is defined as the ratio of the volume occupied by the spheres to the total volume available in the unit cell. It can be expressed mathematically as:
Packing Efficiency=Total Volume OccupiedTotal Volume Available
2. Volume of a Sphere:
The volume V of a single sphere is given by the formula:
V=43πr3
where r is the radius of the sphere.
3. Volume of the Unit Cell:
For a cubic unit cell with edge length a, the volume Vcell is:
Vcell=a3
4. Effective Number of Atoms (Z):
In both hcp and ccp arrangements, the effective number of atoms per unit cell Z is 4.
5. Relationship Between Radius and Edge Length:
For a face-centered cubic (FCC) structure (which is the same as ccp), the relationship between the radius r of the spheres and the edge length a is:
r=√24a
6. Calculating Packing Efficiency:
Substitute the values into the packing efficiency formula:
Packing Efficiency=Z⋅43πr3a3
Substituting Z=4 and r=√24a:
Packing Efficiency=4⋅43π(√24a)3a3
7. Simplifying the Expression:
=4⋅43π⋅2√264a3a3
=4⋅43π⋅√2321
=4⋅π⋅√224
=π√26
8. Calculating Numerical Value:
The numerical value of π√26 is approximately 0.74.
Conclusion:
The available space occupied by spheres of equal size in both hcp and ccp arrangements is approximately 0.74.
Packing efficiency is defined as the ratio of the volume occupied by the spheres to the total volume available in the unit cell. It can be expressed mathematically as:
Packing Efficiency=Total Volume OccupiedTotal Volume Available
The volume V of a single sphere is given by the formula:
V=43πr3
where r is the radius of the sphere.
For a cubic unit cell with edge length a, the volume Vcell is:
Vcell=a3
In both hcp and ccp arrangements, the effective number of atoms per unit cell Z is 4.
For a face-centered cubic (FCC) structure (which is the same as ccp), the relationship between the radius r of the spheres and the edge length a is:
r=√24a
Substitute the values into the packing efficiency formula:
Packing Efficiency=Z⋅43πr3a3
Substituting Z=4 and r=√24a:
Packing Efficiency=4⋅43π(√24a)3a3
=4⋅43π⋅2√264a3a3
=4⋅43π⋅√2321
=4⋅π⋅√224
=π√26
The numerical value of π√26 is approximately 0.74.
The available space occupied by spheres of equal size in both hcp and ccp arrangements is approximately 0.74.
Topper's Solved these Questions
- THE SOLID STATEBOOK - VMC MODULES ENGLISHCHAPTER - THE SOLID STATEEXERCISE - IMPECCABLE
49 Videos
- THE SOLID STATEBOOK - VMC MODULES ENGLISHCHAPTER - THE SOLID STATEEXERCISE - ILLUSTRATIONS
24 Videos
- THE SOLID STATEBOOK - VMC MODULES ENGLISHCHAPTER - THE SOLID STATEEXERCISE - ENABLE
50 Videos
- SURFACE CHEMISTRYBOOK - VMC MODULES ENGLISHCHAPTER - SURFACE CHEMISTRYEXERCISE - PRACTICE EXERCISE
9 Videos
- THEORY OF SOLUTIONSBOOK - VMC MODULES ENGLISHCHAPTER - THEORY OF SOLUTIONSEXERCISE - JEE Advanced (Archive)
31 Videos
Similar Questions
Assertion: Every 4th layer is identical to first layer in ccp pattern of three dimension arrangement
Reason: ABCABC…. Arrangement is present in ccp
View SolutionThe space occupied by b.c.c. arrangement is approximately
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
If the anions (A) form hexagonal close packing and cations (C ) occupy only 2/3rd octahedral voids in it, then the general formula of the compound is
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
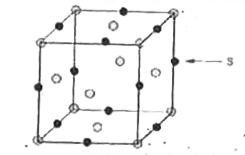
In the figure given below, the site marked as S is a
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
Mark the false statement :
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In Schottky defect
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In the spinel structure, oxide ions are cubic close packed whereas 1/8th of tetrahedral voids are occupied by A2+ cations and 1/2 of octahedral voids are occupied by B3+ cations. The general formula of the compound having spinel structure is
View SolutionCorrect the following statement by changing the underlined part of the sentence.
Three spheres of the first layer and three of the second layer enclose a site at the centre in a closest packing arrangement, the site is called tetrahedral site–––––––––––––––––.
View SolutionA metal crystallizes in a closed packed structure, the atoms stack together occupying maximum space and leaving minimum vacant space. Each sphere in the first layer is in contact with six neighbours. Now while arranging the second layer on the first layer, spheres are placed in depression of first layer. Spheres of third layer lie in the depression of second layer.
This repeating arrangement of atoms produces a giant lattice.
If one of the edge length of unit cell is 'a' what is the shortest distance between two atoms?
View SolutionA metal crystallizes in a closed packed structure, the atoms stack together occupying maximum space and leaving minimum vacant space. Each sphere in the first layer is in contact with six neighbours. Now while arranging the second layer on the first layer, spheres are placed in depression of first layer. Spheres of third layer lie in the depression of second layer.
This repeating arrangement of atoms produces a giant lattice.
If sphere of third layer do not lie directly over the atoms of first layer, then density of unit cell is,
(Given: atomic weight of metal is 197u and a=4.07Å)
View Solution
