A ball is thrown from the top of a 35m high tower with initial velocity of magnitude u=80 ms−1 at an angle 25∘ with horizontal.
Find the time to reach the ground and the horizontal distance covered by the ball.
To solve the problem step by step, we will break it down into manageable parts.
Step 1: Identify the given values
- Height of the tower (h) = 35 m
- Initial velocity (u) = 80 m/s
- Angle of projection (θ) = 25°
Step 2: Calculate the horizontal and vertical components of the initial velocity
1. Horizontal Component (u_x):
ux=u⋅cos(θ)=80⋅cos(25∘)
Using cos(25∘)≈0.9063:
ux=80⋅0.9063≈72.5m/s
2. Vertical Component (u_y):
uy=u⋅sin(θ)=80⋅sin(25∘)
Using sin(25∘)≈0.4226:
uy=80⋅0.4226≈33.8m/s
Step 3: Determine the time of flight (t) until the ball hits the ground
Using the vertical motion equation:
y=uy⋅t+12ay⋅t2
Where:
- y=−35 m (the ball falls down)
- ay=−9.8m/s2 (acceleration due to gravity)
Substituting the values:
−35=33.8⋅t−12⋅9.8⋅t2
Rearranging gives:
4.9t2−33.8t−35=0
Step 4: Solve the quadratic equation for t
Using the quadratic formula t=−b±√b2−4ac2a:
- Here, a=4.9, b=−33.8, c=−35.
Calculating the discriminant:
b2−4ac=(−33.8)2−4⋅4.9⋅(−35)
=1142.44+686=1828.44
Now substituting into the quadratic formula:
t=33.8±√1828.442⋅4.9
Calculating √1828.44≈42.7:
t=33.8±42.79.8
Taking the positive root:
t=76.59.8≈7.8s
Step 5: Calculate the horizontal distance (R) covered by the ball
Using the horizontal motion equation:
R=ux⋅t
Substituting the values:
R=72.5⋅7.8≈566.55m
Final Answers
- Time to reach the ground: t≈7.8s
- Horizontal distance covered: R≈566.55m
---
- Height of the tower (h) = 35 m
- Initial velocity (u) = 80 m/s
- Angle of projection (θ) = 25°
1. Horizontal Component (u_x):
ux=u⋅cos(θ)=80⋅cos(25∘)
Using cos(25∘)≈0.9063:
ux=80⋅0.9063≈72.5m/s
uy=u⋅sin(θ)=80⋅sin(25∘)
Using sin(25∘)≈0.4226:
uy=80⋅0.4226≈33.8m/s
Using the vertical motion equation:
y=uy⋅t+12ay⋅t2
Where:
- y=−35 m (the ball falls down)
- ay=−9.8m/s2 (acceleration due to gravity)
−35=33.8⋅t−12⋅9.8⋅t2
Rearranging gives:
4.9t2−33.8t−35=0
Using the quadratic formula t=−b±√b2−4ac2a:
- Here, a=4.9, b=−33.8, c=−35.
b2−4ac=(−33.8)2−4⋅4.9⋅(−35)
=1142.44+686=1828.44
t=33.8±√1828.442⋅4.9
Calculating √1828.44≈42.7:
t=33.8±42.79.8
t=76.59.8≈7.8s
Using the horizontal motion equation:
R=ux⋅t
Substituting the values:
R=72.5⋅7.8≈566.55m
- Time to reach the ground: t≈7.8s
- Horizontal distance covered: R≈566.55m
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - SOLVED EXAMPLES20videos
Motion in Straight Line
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - PRACTICE EXERCISE80videos
Motion in Straight Line
- BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - IMPECCABLE52videos
MOTION IN A STRAIGHT LINE & PLANE
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ2videos
Motion in Two Dimensions
Similar Questions
A ball is thrown from the top of 36m high tower with velocity 5m/ss at an angle 37∘ above the horizontal as shown. Its horizontal distance on the ground is closest to [g=10m/s2
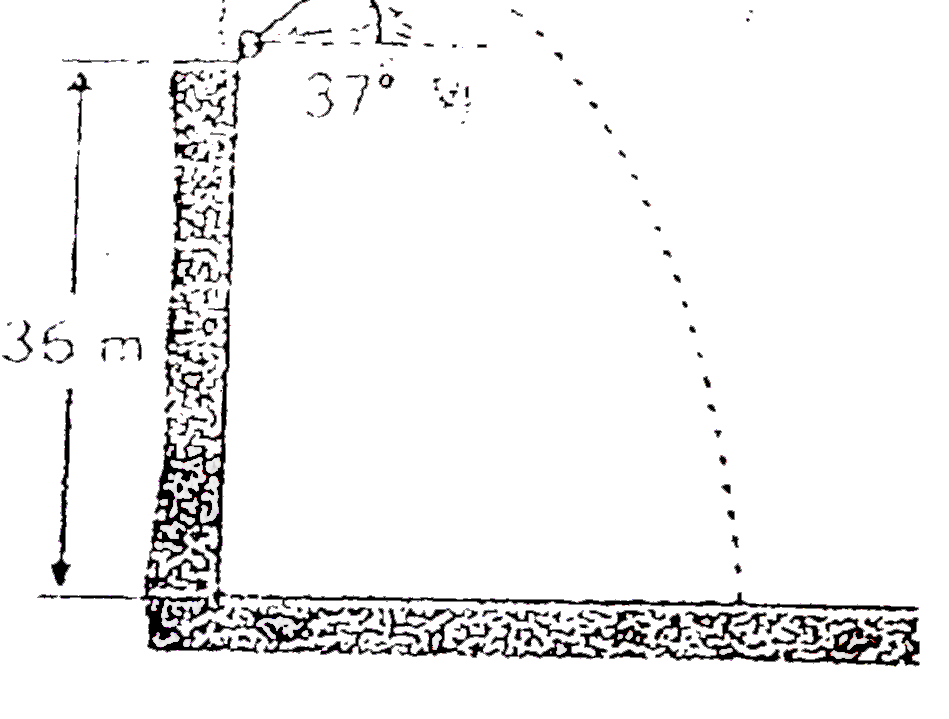 : View Solution
: View SolutionA ball is projected horizontal from the top of a tower with a velocity v0. It will be moving at an angle of 60∘ with the horizontal after time.
View Solution
Knowledge Check
- Question 1 - Select One
A ball is thrown from the top of a tower with an initial velocity of 10m/s at an angle of 30∘above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower (g=10m/s2) will be
A5 mB20 mC15 mD10 m
A bullet is projected upwards from the top of a tower of height 90 m with the velocity 30ms−1 making an angle 30∘ with the horizontal. Find the time taken by it to reach the ground is (g=10ms−2)
View SolutionA ball is thrown from the top of a tower with an intial velocity of 10 m//s at an angle 37∘ above the horizontal, hits the ground at a distance 16 m from the base of tower. Calculate height of tower. [g=10m/s2]
View SolutionA ball is projected upwards from the top of a tower with a velocity 50ms−1 making an angle 30∘ with the horizontal. The height of tower is 70m. After how many seconds from the instant of throwing, will the ball reach the ground. (g=10ms−2)
View SolutionA ball is projected upwards from the top of a tower with a velocity 50ms−1 making an angle 30∘ with the horizontal. The height of tower is 70m. After how many seconds from the instant of throwing, will the ball reach the ground. (g=10ms−2)
View SolutionA boy throws a ball with a velocity of 15 m/s at an angle of 15° with the horizontal. The distance at which the ball strikes the ground is
View SolutionA ball is thrown vertically upwards from the top of a tower with an initial velocity of 19.6 ms−1 . The ball reaches the ground after 5s. Calculate the height of the tower .
View SolutionA ball is throw from the top of a tower of 61 m high with a velocity 24.4ms−1 at an elevation of 30∘ above the horizon. What is the distance from the foot of the tower to the point where the ball hits the ground ?
View Solution

