The engine of a train passes an electric pole with a velocity 'u' and the last compartment of the train crosses the same pole with a velocity v. Then find the velocity with which the mid-point of the train passes the pole. Assume acceleration to be uniform.
To solve the problem, we need to find the velocity with which the midpoint of the train passes the electric pole, given that the engine passes the pole with velocity u and the last compartment passes with velocity v. We will assume that the train is moving with uniform acceleration.
1. Understand the Setup:
- Let the train have a length L.
- The engine (front) of the train passes the pole with velocity u.
- The last compartment (rear) of the train passes the pole with velocity v.
- The midpoint of the train is at a distance L2 from both the engine and the last compartment.
2. Define Variables:
- Let vm be the velocity of the midpoint of the train as it passes the pole.
- The distance traveled by the engine to the pole is 0 (as it just passes the pole).
- The distance traveled by the last compartment to the pole is L.
3. Use the Kinematic Equation:
- Since the train is accelerating uniformly, we can use the kinematic equation:
v2=u2+2as
- For the midpoint, we can set up two equations based on the distances traveled.
4. Equation for the Engine:
- For the engine:
v2m=u2+2a(L2)
- This simplifies to:
v2m=u2+aL (Equation 1)
5. Equation for the Last Compartment:
- For the last compartment:
v2=v2m+2aL
- Rearranging gives:
v2m=v2−2aL (Equation 2)
6. Equate the Two Expressions for v2m:
- From Equation 1 and Equation 2, we have:
u2+aL=v2−2aL
- Rearranging gives:
u2+3aL=v2
7. Solve for a:
- From the above equation, we can express a:
a=v2−u23L
8. Substituting a back into v2m:
- Substitute a back into either Equation 1 or Equation 2 to find vm:
v2m=u2+(v2−u23L)L
- Simplifying gives:
v2m=u2+v2−u23
- This can be rearranged to:
v2m=3u2+v2−u23=2u2+v23
9. Final Expression for vm:
- Taking the square root gives:
vm=√u2+v22
Final Answer:
The velocity with which the midpoint of the train passes the pole is:
vm=√u2+v22
- Let the train have a length L.
- The engine (front) of the train passes the pole with velocity u.
- The last compartment (rear) of the train passes the pole with velocity v.
- The midpoint of the train is at a distance L2 from both the engine and the last compartment.
- Let vm be the velocity of the midpoint of the train as it passes the pole.
- The distance traveled by the engine to the pole is 0 (as it just passes the pole).
- The distance traveled by the last compartment to the pole is L.
- Since the train is accelerating uniformly, we can use the kinematic equation:
v2=u2+2as
- For the midpoint, we can set up two equations based on the distances traveled.
- For the engine:
v2m=u2+2a(L2)
- This simplifies to:
v2m=u2+aL (Equation 1)
- For the last compartment:
v2=v2m+2aL
- Rearranging gives:
v2m=v2−2aL (Equation 2)
- From Equation 1 and Equation 2, we have:
u2+aL=v2−2aL
- Rearranging gives:
u2+3aL=v2
- From the above equation, we can express a:
a=v2−u23L
- Substitute a back into either Equation 1 or Equation 2 to find vm:
v2m=u2+(v2−u23L)L
- Simplifying gives:
v2m=u2+v2−u23
- This can be rearranged to:
v2m=3u2+v2−u23=2u2+v23
- Taking the square root gives:
vm=√u2+v22
The velocity with which the midpoint of the train passes the pole is:
vm=√u2+v22
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-A11videos
Motion in Straight Line
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-B10videos
Motion in Straight Line
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - SOLVED EXAMPLES20videos
Motion in Straight Line
- BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - IMPECCABLE52videos
MOTION IN A STRAIGHT LINE & PLANE
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ2videos
Motion in Two Dimensions
Similar Questions
The two ends of a train moving with uniform acceleration pass a certain point with velocity u and v. Find the velocity with which the middle point of the train passes the same point.
View SolutionThe two ends of a train moving with constant acceleration pass a certain point with velocities u and 3u. The velocity with which the middle point of the train passes the same point is
View SolutionEngine of a train that is moving with unifrom acceleration passes a pole with speed u while the last compartment passes the pole with speed 'v'. The middle point of the train passes the given pole with speed:
View SolutionA train is moving with uniform acceleration. The two ends of the train pass through a point on the track with velocity v1 and v2. With what velocity the middle point of the train would pass through the same point ?
View SolutionA train 200m long is moving with a velocity of 72kmh−1 Find the time taken by the train to cross the bridge 1km long .
View SolutionThe diagram shows a train moving with constant velocity and a car moving towards the train with constant velocity. The engine driver measures the velocity of the car as v1 . The passenger sitting in the last compartment measures the velocity of the car as v2 . Which of the following statements is true?
 View Solution
View SolutionA person standing on a platform finds that a train moving with velocity, 0.6c takes one second to pass by him. Find (a) the length of the train as seen by the person and (b) the rest length of the train .
View SolutionA car is moving with velocity →vc towards north and a train is moving towards east with velocity →vt . Find the direction of relative velocity of car with respect to train.
View SolutionA boy on a train of height h1 projects a coin his friend of height h2 standing on the same train, with a velocity v relative to the train, at an angle θ with horizontal. If the train moves with a constant velocity v' in the direction of x - motion of the coin, find the
(a) distance between the boys so that the second boy can catch the coin,
(b) maximum height attained by the coin, and
( c) speed with which the second boy catches the coin relative to himself (train) and ground.View SolutionIn the figure the top view of a compartment of a train is shown. A man is sitting at a corner 'B' of the compartment . The man throws a ball ( with respect to himself ) along the surface of the floor towards the corner 'D' of the compartment of the train. The ball hits the corner 'A' of the compartment, then find the time at which it hits A after the ball is thrown . Assume no other collision during motion and floor is smooth. The length of the compartment is given 'l' and the train is moving with constant acceleration 'a' in the direction shown in the figure.
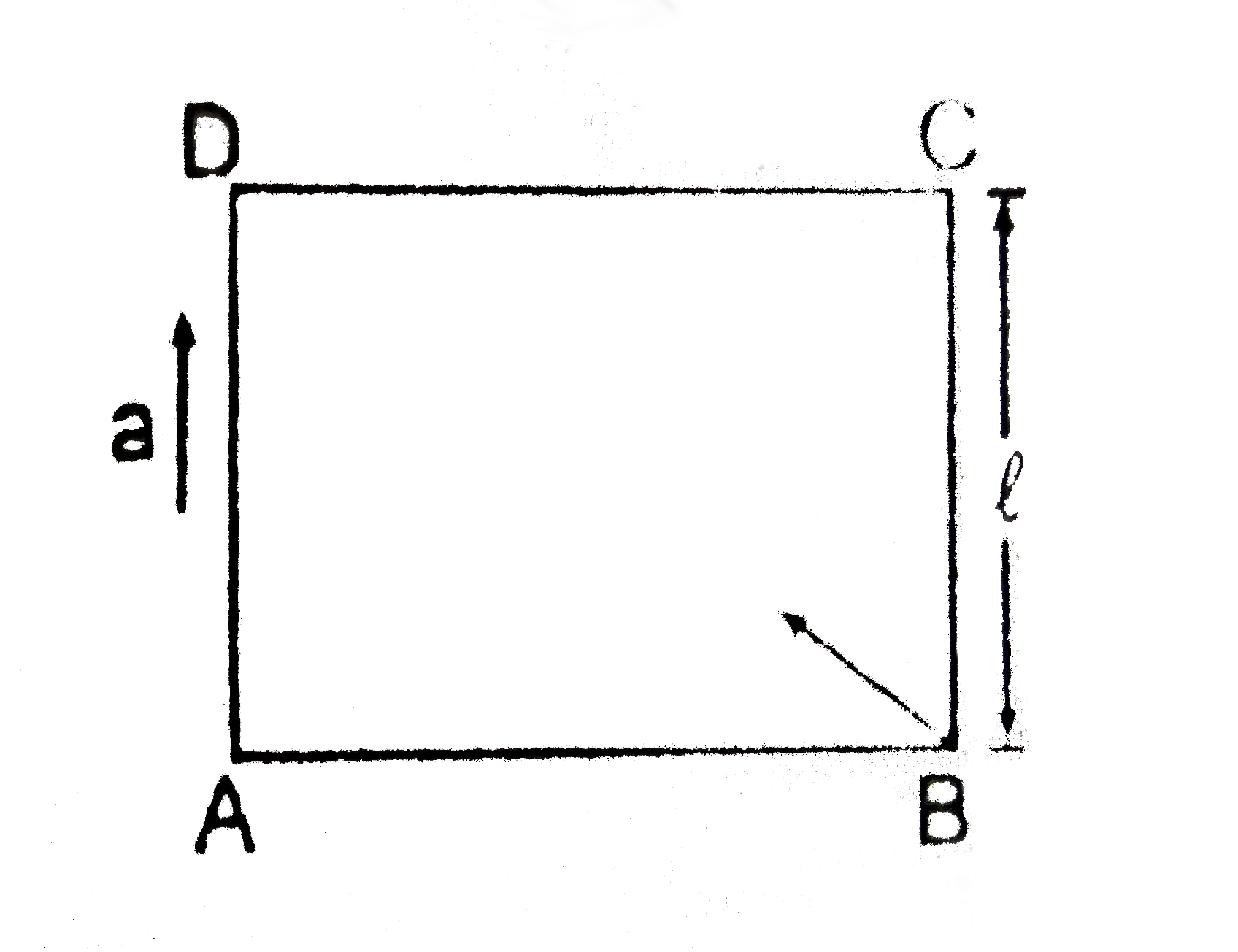 View Solution
View Solution

