A train is moving with uniform acceleration. The two ends of the train pass through a point on the track with velocity v1 and v2. With what velocity the middle point of the train would pass through the same point ?
[v21+v222]12
(v21−v22)2
v1+v22
v1−v22
The correct Answer is:A
To solve the problem of finding the velocity with which the middle point of the train passes through the same point, we will use the equations of motion under uniform acceleration.
1. Understanding the Problem:
- We have a train moving with uniform acceleration.
- The front end of the train passes a point with velocity v1.
- The back end of the train passes the same point with velocity v2.
- We need to find the velocity vm of the middle point of the train as it passes through the same point.
2. Using the Third Equation of Motion:
- The third equation of motion states:
v2=u2+2as
- Here, v is the final velocity, u is the initial velocity, a is the acceleration, and s is the distance.
3. Applying the Equation for the Back End of the Train:
- For the back end of the train (velocity v2):
v22=v21+2aL
- This equation relates the velocities and acceleration over the length L of the train.
4. Applying the Equation for the Middle Point of the Train:
- For the middle point of the train (velocity vm):
v2m=v21+2a(L2)
- This equation accounts for the distance covered by the middle point, which is half the length of the train.
5. Rearranging the Equations:
- From the first equation:
v22=v21+2aL(Equation 1)
- From the second equation:
v2m=v21+aL(Equation 2)
6. Subtracting Equation 1 from Equation 2:
- We can express v2m in terms of v1 and v2:
v2m=v21+v222
7. Final Expression for the Velocity of the Middle Point:
- Taking the square root gives:
vm=√v21+v222
Final Answer:
The velocity with which the middle point of the train passes through the same point is:
vm=√v21+v222
- We have a train moving with uniform acceleration.
- The front end of the train passes a point with velocity v1.
- The back end of the train passes the same point with velocity v2.
- We need to find the velocity vm of the middle point of the train as it passes through the same point.
- The third equation of motion states:
v2=u2+2as
- Here, v is the final velocity, u is the initial velocity, a is the acceleration, and s is the distance.
- For the back end of the train (velocity v2):
v22=v21+2aL
- This equation relates the velocities and acceleration over the length L of the train.
- For the middle point of the train (velocity vm):
v2m=v21+2a(L2)
- This equation accounts for the distance covered by the middle point, which is half the length of the train.
- From the first equation:
v22=v21+2aL(Equation 1)
- From the second equation:
v2m=v21+aL(Equation 2)
- We can express v2m in terms of v1 and v2:
v2m=v21+v222
- Taking the square root gives:
vm=√v21+v222
The velocity with which the middle point of the train passes through the same point is:
vm=√v21+v222
Topper's Solved these Questions
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - C)
7 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - D)
24 Videos
- MOTION IN STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN STRAIGHT LINEEXERCISE - Assignment (SECTION - A)
50 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
Similar Questions
The two ends of a train moving with uniform acceleration pass a certain point with velocity u and v. Find the velocity with which the middle point of the train passes the same point.
View SolutionThe two ends of a train moving with constant acceleration pass a certain point with velocities u and 3u. The velocity with which the middle point of the train passes the same point is
View Solution
Knowledge Check
If the figure, what is the slope of line passing through the two points?
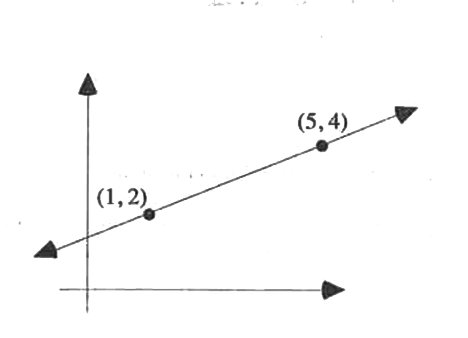 A1/4B1C1/2D3/2
A1/4B1C1/2D3/2A train starting from rest, and moving with uniform acceleration α, acquires a speed v. Then its comes to a stop with uniform retardation β. Then the average velocity of the train is
Av/2Bv/4C(α+β)t/2D(α+β)t/αβ
Engine of a train that is moving with unifrom acceleration passes a pole with speed u while the last compartment passes the pole with speed 'v'. The middle point of the train passes the given pole with speed:
View SolutionThe engine of a train passes an electric pole with a velocity 'u' and the last compartment of the train crosses the same pole with a velocity v. Then find the velocity with which the mid-point of the train passes the pole. Assume acceleration to be uniform.
View SolutionA particle moving with uniform acceleration from A to B along a straight line has velcities v1 and v2 at A and B respectively. If C is the mid-point between A and B then determine the velocity of the particle at C .
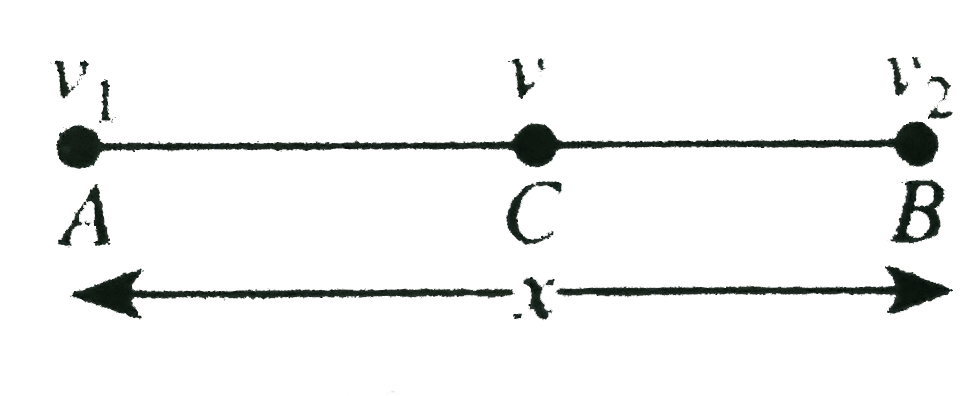 .
.
View SolutionA car is moving with velocity →vc towards north and a train is moving towards east with velocity →vt . Find the direction of relative velocity of car with respect to train.
View SolutionAn open carriage in a goods train is moving with a uniform velocity of 10 m/s. If the rain adds water with zero velocity at the rate of 5 kg/s, then the additional force required by the engine to maintain the same velocity of the train is
View SolutionTwo particles move in a uniform gravitational field with an acceleration g. At the intial moment the particles were located at one point and moved with velocity v1=1 ms−1 and v2=4 ms−1 horizontally in opposite directions. Find the time interval after their velocity vectors become mutually perpendicular
View Solution