Position of a particle moving along x-axis is given by x=2+8t−4t2. The distance travelled by the particle from t=0 to t=2 is:-
0
8
12
16
The correct Answer is:B
To solve the problem of finding the distance traveled by a particle moving along the x-axis given its position function x(t)=2+8t−4t2, we will follow these steps:
Step 1: Find the velocity function
The velocity v(t) is the derivative of the position function x(t) with respect to time t.
v(t)=dxdt=ddt(2+8t−4t2)=0+8−8t=8−8t
Step 2: Determine the time intervals when the particle changes direction
To find when the particle changes direction, we need to find when the velocity is zero.
8−8t=0⟹t=1 second
Step 3: Calculate the position at t=0, t=1, and t=2
Now we will calculate the position of the particle at these times.
- At t=0:
x(0)=2+8(0)−4(0)2=2
- At t=1:
x(1)=2+8(1)−4(1)2=2+8−4=6
- At t=2:
x(2)=2+8(2)−4(2)2=2+16−16=2
Step 4: Calculate the distance traveled
The distance traveled by the particle from t=0 to t=2 can be calculated by finding the total distance covered in the intervals (0,1) and (1,2).
1. From t=0 to t=1:
Distance=x(1)−x(0)=6−2=4 meters
2. From t=1 to t=2:
Distance=x(2)−x(1)=2−6=−4 meters
Since distance cannot be negative, we take the absolute value:
Distance=4 meters
Step 5: Total distance traveled
Now, we add the distances from both intervals:
Total Distance=4+4=8 meters
Thus, the distance traveled by the particle from t=0 to t=2 is 8 meters.
Final Answer:
The distance traveled by the particle from t=0 to t=2 is 8 meters.
---
The velocity v(t) is the derivative of the position function x(t) with respect to time t.
To find when the particle changes direction, we need to find when the velocity is zero.
Now we will calculate the position of the particle at these times.
x(0)=2+8(0)−4(0)2=2
x(1)=2+8(1)−4(1)2=2+8−4=6
x(2)=2+8(2)−4(2)2=2+16−16=2
The distance traveled by the particle from t=0 to t=2 can be calculated by finding the total distance covered in the intervals (0,1) and (1,2).
Distance=x(1)−x(0)=6−2=4 meters
Distance=x(2)−x(1)=2−6=−4 meters
Since distance cannot be negative, we take the absolute value:
Distance=4 meters
Now, we add the distances from both intervals:
Total Distance=4+4=8 meters
The distance traveled by the particle from t=0 to t=2 is 8 meters.
Topper's Solved these Questions
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-C
10 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-D
10 Videos
- Motion in Straight Line BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Straight Line EXERCISE - IN-CHAPTER EXERCISE-A
11 Videos
- MOTION IN A STRAIGHT LINE & PLANE BOOK - VMC MODULES ENGLISHCHAPTER - MOTION IN A STRAIGHT LINE & PLANE EXERCISE - IMPECCABLE
52 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
Similar Questions
Position of particle moving along x-axis is given as x=2+5t+7t2 then calculate :
View SolutionThe position of a particle along x-axis at time t is given by x=1+t−t2. The distance travelled by the particle in first 2 seconds is
View SolutionThe position of a particle moving along x-axis is given by x=10t−2t2. Then the time (t) at which it will momentily come to rest is
View Solution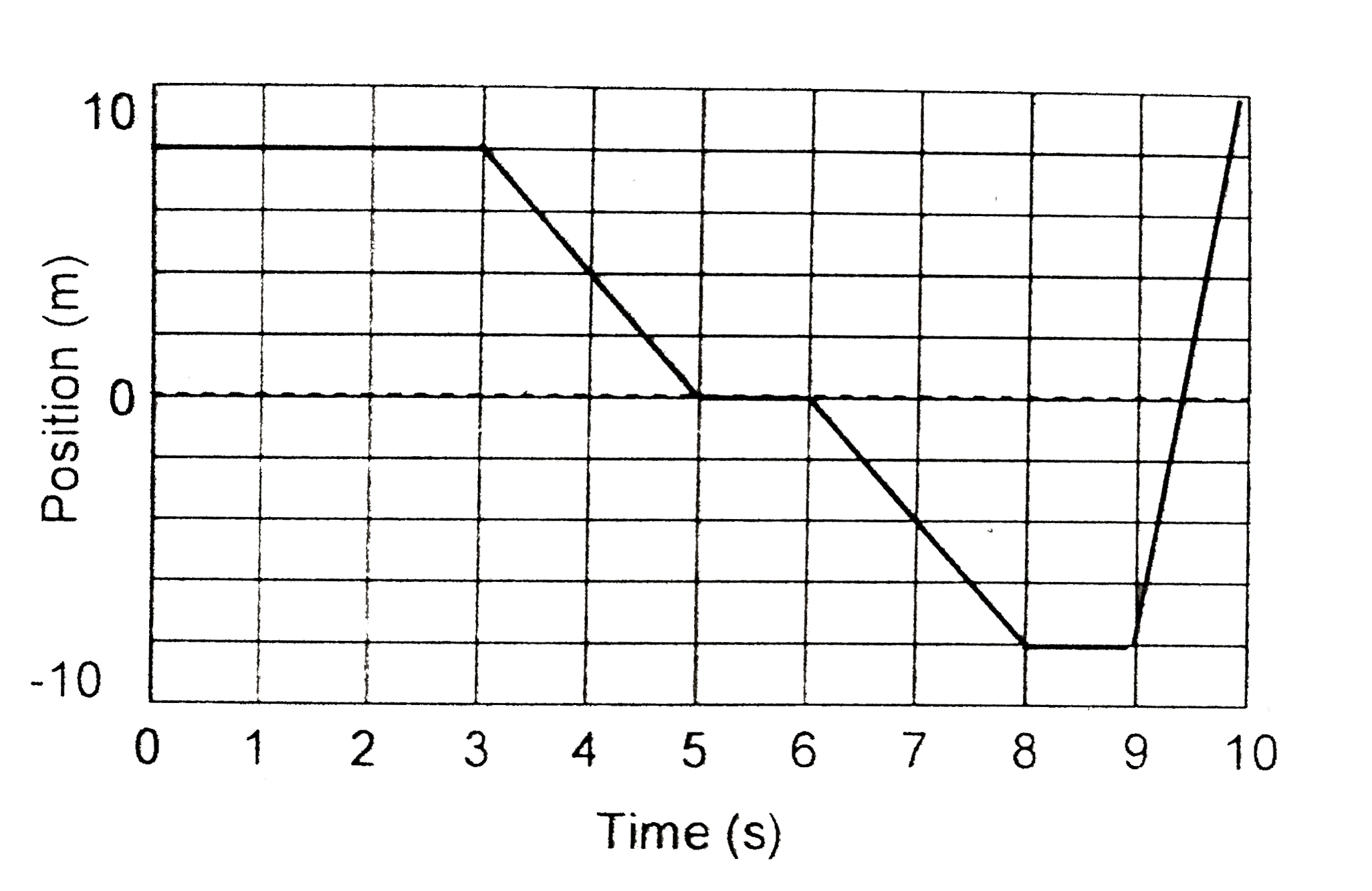
The position versus time graph of a particle moving along a straight line is shown. What is the total distance travelled by the particle from t=0s to t=10s?
View SolutionThe position of a particle along X-axis at time t is given by x=2+t−3t2. The displacement and the distance travelled in the interval, t = 0 to t = 1 are respectively
View SolutionA particle moves on x-axis as per equation x=(t3−9t2+15+2)m. Distance travelled by the particle between t=0 and t=5s is
View SolutionA particle moves along a straight line on y-axis. The distance of the particle from O varies with time and is given by : y=20t−t2. The distance travelled by the particle before it momentarily comes to rest is
View SolutionThe position of a particle moving along x-axis given by x=(−2t3−3t2+5)m. The acceleration of particle at the instant its velocity becomes zero is
View SolutionVelocity time equation of a particle moving in a straight line is v=2t−4 for t≤2s and v=4−2t for t>2.The distance travelled by the particle in the time interval from t=0 to t=4s is (Here t is in second and v in m/s)
View SolutionIf the velocity of a paraticle moving along x-axis is given as v=(4t2+3t=1)m/s then acceleration of the particle at t=1sec is :
View Solution
