A particle of mass 1 kg is moving along the line y=x+2 (here x and y are in metres) with speed 2m/s. The magnitude of angular momentum of paticle about origin is -
To find the magnitude of angular momentum of a particle about the origin, we can use the formula for angular momentum L:
L=m⋅v⋅r
where:
- L is the angular momentum,
- m is the mass of the particle,
- v is the speed of the particle,
- r is the perpendicular distance from the line of motion to the axis of rotation (in this case, the origin).
1. Identify the mass and speed of the particle:
- Given mass m=1kg
- Given speed v=2m/s
2. Determine the line of motion:
- The particle is moving along the line y=x+2.
3. Find the perpendicular distance from the origin to the line:
- The line can be rewritten in the standard form Ax+By+C=0:
x−y+2=0(where A=1,B=−1,C=2)
- The formula for the perpendicular distance r from a point (x0,y0) to the line Ax+By+C=0 is given by:
r=|Ax0+By0+C|√A2+B2
- Substituting the origin (0,0):
r=|1⋅0+(−1)⋅0+2|√12+(−1)2=|2|√2=2√2=√2m
4. Calculate the angular momentum:
- Now substituting m=1kg, v=2m/s, and r=√2m into the angular momentum formula:
L=m⋅v⋅r=1⋅2⋅√2=2√2kg m2/s
5. Final Answer:
- The magnitude of angular momentum of the particle about the origin is 2√2kg m2/s.
- L is the angular momentum,
- m is the mass of the particle,
- v is the speed of the particle,
- r is the perpendicular distance from the line of motion to the axis of rotation (in this case, the origin).
- Given mass m=1kg
- Given speed v=2m/s
- The particle is moving along the line y=x+2.
- The line can be rewritten in the standard form Ax+By+C=0:
x−y+2=0(where A=1,B=−1,C=2)
- The formula for the perpendicular distance r from a point (x0,y0) to the line Ax+By+C=0 is given by:
r=|Ax0+By0+C|√A2+B2
- Substituting the origin (0,0):
r=|1⋅0+(−1)⋅0+2|√12+(−1)2=|2|√2=2√2=√2m
- Now substituting m=1kg, v=2m/s, and r=√2m into the angular momentum formula:
L=m⋅v⋅r=1⋅2⋅√2=2√2kg m2/s
- The magnitude of angular momentum of the particle about the origin is 2√2kg m2/s.
Topper's Solved these Questions
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES
20 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - PRACTICE EXERCISE-1
4 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - IMPECCABLE
56 Videos
Similar Questions
A particle mass 1 kg is moving along a straight line y=x+4. Both x and y are in metres. Velocity of the particle is 2m/s. Find the magnitude of angular momentum of the particle about origin.
View SolutionA particle of mass m=3kg moves along a straight line 4y−3x=2 where x and y are in metre, with constant velocity v=5ms−1 the magnitude of angular momentum about the origin is
View SolutionA body of mass 10 kg moves along a straight line y=x+5, where x and y are in metres with velocity 2 m/s. Its angular momentum about a point having co-ordinate (0,1) is
View SolutionA particle of mass m is moving along the line y=b,z=0 with constant speed v. State whether the angular momentum of particle about origin is increasing, decreasing or constant.
View SolutionA particle of mass m is moving along the line y=b,z=0 with constant speed v. State whether the angular momentum of particle about origin is increasing. Decreasing or constant.
View SolutionA particle of mass m=5 units is moving with a uniform speed v=3√2 units in the XY-plane along the y=x+4. The magnitude of the angular momentum about origin is
View SolutionA particle of mass 5g is moving with a uniform speed of 3√2cm/s in the x−y plane along the line y=x+4. The magnitude of its angular momentum about the origin in gcm2/s is
View SolutionA particle of mass 300 g is moving with a speed of 20 ms−1 along the straight line y = x - 4√2. The angular momentum of the particle about the origin is (where y & x are in metres)
View SolutionA disc of mass M and Radius R is rolling with an angular speed ω on the horizontal plane. The magnitude of angular momentum of the disc about origin is:
View SolutionA cube of mass m and side a is moving along a plane with constant speed vo as shown in figure. The magnitude of angular momentum of the cube about z -axis would be.
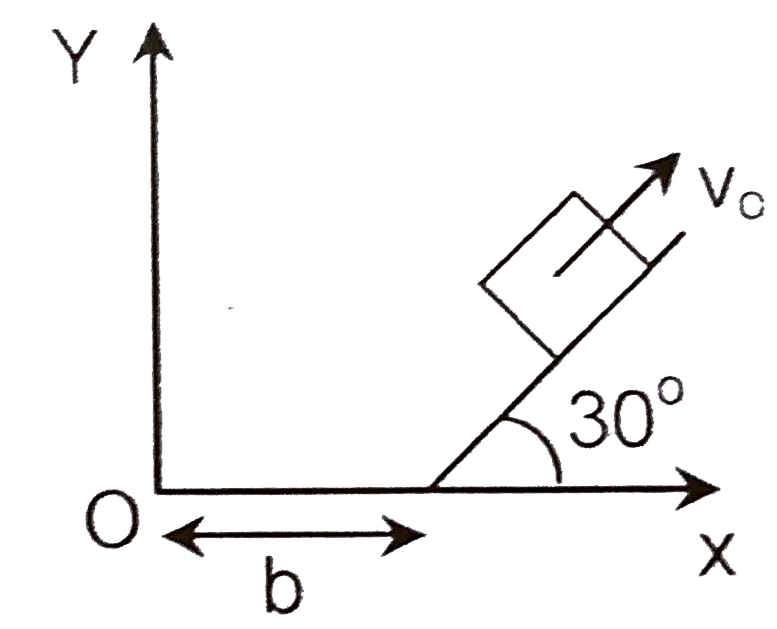
View Solution
