A disc rolls down a plane of length L and inclined at angle θ, without slipping. Its velocity on reaching the bottom will be :-
√(4gLsinθ)/3
√(2gLsinθ)/3
√(10gLsinθ)/7
√(4gLsinθ)
The correct Answer is:A
To solve the problem of a disc rolling down an inclined plane without slipping, we can use the principle of conservation of energy. Here’s a step-by-step solution:
Step 1: Identify the energies at the top and bottom of the incline
At the top of the incline (point A), the disc has potential energy and no kinetic energy (since it starts from rest). At the bottom of the incline (point B), the disc has kinetic energy due to both translation and rotation.
- Potential Energy at A: PEA=mgh
- Kinetic Energy at B: KEB=12mv2+12Iω2
Step 2: Determine the height (h) in terms of L and θ
The height (h) can be expressed in terms of the length of the incline (L) and the angle (θ):
h=Lsin(θ)
Step 3: Write the energy conservation equation
According to the conservation of energy:
PEA=KEB
Substituting the expressions for potential and kinetic energy:
mgh=12mv2+12Iω2
Step 4: Substitute for I and ω
For a disc, the moment of inertia I is given by:
I=12mr2
In pure rolling motion, the relationship between linear velocity v and angular velocity ω is:
ω=vr
Substituting ω into the kinetic energy equation:
KEB=12mv2+12(12mr2)(vr)2
This simplifies to:
KEB=12mv2+14mv2=34mv2
Step 5: Substitute h into the energy equation
Now substituting h into the energy conservation equation:
mg(Lsin(θ))=34mv2
Step 6: Cancel mass and solve for v
Canceling m from both sides:
gLsin(θ)=34v2
Now, solving for v2:
v2=4gLsin(θ)3
Step 7: Take the square root to find v
Taking the square root gives:
v=√4gLsin(θ)3
Final Answer
Thus, the velocity of the disc on reaching the bottom of the incline is:
v=2√gLsin(θ)√3
At the top of the incline (point A), the disc has potential energy and no kinetic energy (since it starts from rest). At the bottom of the incline (point B), the disc has kinetic energy due to both translation and rotation.
- Kinetic Energy at B: KEB=12mv2+12Iω2
The height (h) can be expressed in terms of the length of the incline (L) and the angle (θ):
h=Lsin(θ)
According to the conservation of energy:
PEA=KEB
Substituting the expressions for potential and kinetic energy:
mgh=12mv2+12Iω2
For a disc, the moment of inertia I is given by:
I=12mr2
In pure rolling motion, the relationship between linear velocity v and angular velocity ω is:
ω=vr
Substituting ω into the kinetic energy equation:
KEB=12mv2+12(12mr2)(vr)2
This simplifies to:
KEB=12mv2+14mv2=34mv2
Now substituting h into the energy conservation equation:
mg(Lsin(θ))=34mv2
Canceling m from both sides:
gLsin(θ)=34v2
Now, solving for v2:
v2=4gLsin(θ)3
Taking the square root gives:
v=√4gLsin(θ)3
Thus, the velocity of the disc on reaching the bottom of the incline is:
v=2√gLsin(θ)√3
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - ENABLE
50 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - EFFICIENT
50 Videos
- SYSTEM OF A PARTICLES & ROTATIONAL MOTIONBOOK - VMC MODULES ENGLISHCHAPTER - SYSTEM OF A PARTICLES & ROTATIONAL MOTIONEXERCISE - IN-CHAPTER EXERCISE F
10 Videos
- UNITS, MEASUREMENTS & ERRORSBOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B
10 Videos
Similar Questions
Knowledge Check
A solid cylinder of mass M and radius R rolls down an inclined plane without slipping. THE speed of its centre of mass when it reaches the bottom is
A√(2gh)B√4/3.ghC√3/4.ghD√(4g/h)
A block moves down a smooth inclined plane of inclination θ. Its velocity on reaching the bottom is v. If it slides down a rough inclined plane of some inclination, its velocity on reaching the bottom is v/n, where n is a number greater than 0. The coefficient of friction is given by -
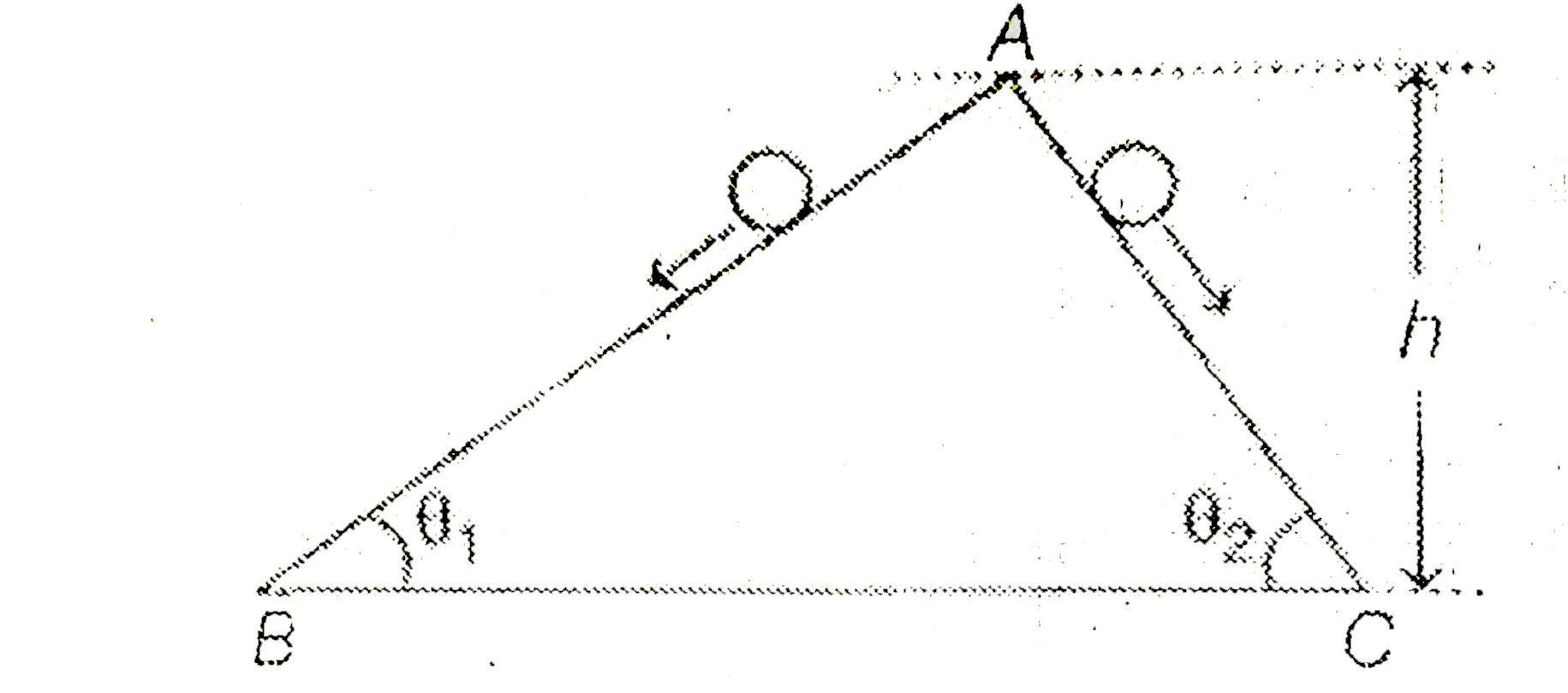
View SolutionA small disc is released from rest at A on an inclined plane AB so that it rolls down without slipping. It reaches the bottom with linear velocity v1 in time t1. Next a small ring released form rest on the inclined plane AC so that it rolls down without slipping. It reaches the bottom with linear vlocity v2 in time t2. Given θ1=30∘,θ2=60∘, and h=10m. Then,
View SolutionA solid cylinder of mass M and radius R rolls from rest down a plane inclined at an angle θ to the horizontal. The velocity of the centre of mass of the cylinder after it has rolled down a distance d is :
View SolutionA disc of mass 3 kg rolls down an inclined plane of height 5 m. The translational kinetic energy of the disc on reaching the bottom of the inclined plane is
View SolutionIf a ring, a disc, a solid sphere and a cyclinder of same radius roll down an inclined plane, the first one to reach the bottom will be:
View SolutionA thin uniform circular ring is rolling down an inclined plane of inclination 30∘ without slipping. Its linear acceleration along the inclined plane will be
View SolutionA thin uniform circular ring is rolling down an inclined plane of inclination 30∘ without slipping. Its linear acceleration along the inclined plane will be
View Solution
