Current I flows through solenoid of length L having N number of turns, when it is connected to DC emf. If charged particle is projected along the axis of solenoid with a speed v0, them find the force on the charged particle in the solenoid.
To find the force on a charged particle projected along the axis of a solenoid carrying a current, we can follow these steps:
Step 1: Understand the Magnetic Field Inside the Solenoid
A solenoid produces a uniform magnetic field inside it when a current flows through it. The magnetic field B inside a long solenoid can be given by the formula:
B=μ0NLI
where:
- μ0 is the permeability of free space (4π×10−7T m/A),
- N is the number of turns,
- L is the length of the solenoid,
- I is the current flowing through the solenoid.
Step 2: Identify the Force on the Charged Particle
The force F acting on a charged particle moving in a magnetic field is given by the Lorentz force equation:
F=q(v×B)
where:
- q is the charge of the particle,
- v is the velocity vector of the particle,
- B is the magnetic field vector.
Step 3: Analyze the Direction of Motion
In this case, the charged particle is projected along the axis of the solenoid, which means its velocity v is parallel to the magnetic field B inside the solenoid.
Step 4: Calculate the Angle Between v and B
Since the velocity of the charged particle and the magnetic field are parallel, the angle θ between them is:
θ=0∘
Step 5: Substitute into the Lorentz Force Equation
The sine of the angle θ is:
sin(0∘)=0
Substituting this into the force equation gives:
F=qvBsin(0∘)=qvB⋅0=0
Conclusion
Thus, the force acting on the charged particle when it is projected along the axis of the solenoid is:
F=0
A solenoid produces a uniform magnetic field inside it when a current flows through it. The magnetic field B inside a long solenoid can be given by the formula:
B=μ0NLI
where:
- μ0 is the permeability of free space (4π×10−7T m/A),
- N is the number of turns,
- L is the length of the solenoid,
- I is the current flowing through the solenoid.
The force F acting on a charged particle moving in a magnetic field is given by the Lorentz force equation:
F=q(v×B)
where:
- q is the charge of the particle,
- v is the velocity vector of the particle,
- B is the magnetic field vector.
In this case, the charged particle is projected along the axis of the solenoid, which means its velocity v is parallel to the magnetic field B inside the solenoid.
Since the velocity of the charged particle and the magnetic field are parallel, the angle θ between them is:
θ=0∘
The sine of the angle θ is:
sin(0∘)=0
Substituting this into the force equation gives:
F=qvBsin(0∘)=qvB⋅0=0
Thus, the force acting on the charged particle when it is projected along the axis of the solenoid is:
F=0
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - SOLVED EXAMPLES20videos
MOVING CHARGES & MAGNETISM
- BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - PRACTICE EXERCISE 11videos
MOVING CHARGES & MAGNETISM
- BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IMPECCABLE53videos
MOVING CHARGES & MAGNETISM
- BOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ2videos
Motion in Two Dimensions
- BOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)1videos
PROPERTIES OF MATTER
Similar Questions
A thin solenoid of length 0.4m and having 500 turns of wire carries a current 1A,then find the magnetic field on the axis inside the solenoid.
View SolutionA tightly- wound, long solenoid is kept with its axis parallel to a large metal sheet carrying a surface current. The surgace current through a width dl of the sheet is Kdl and the number of turns per unit length of the solenoid is n. The magnetic field near the centre of the solenoid is found to be zero. (a) find the current in the solenoid. (b) If the solenoid is rotated to make its axis perpendicular to the metal sheet, what would be the magnitude of the magnetic field near its centre?
View SolutionIf a charged particle is projected on a rough horizontal surface with speed v0. Find the value of dynamic coefficient of friction, if the kinetic energy of system is constant.
 View Solution
View SolutionA long solenoid of length l=2.0 m , radius r=0.1 m and total number of turns N=1000 is carrying a current i0=20.0A. The axis of the solenoid coincides with the z-axis.
(a) State the expression for the magnetic field of the solenoid and calculate its value ? Magnetic field.
(b) Obtain the expression for the self - inductance (L) of the solenoid. Calculate its value. Value of L .View SolutionAn electron gun is placed inside a long solenoid of radius R on its exis. The solenoid has n turns/Length and carries a current I. The electron gun schoots an electron along the radius of the solenoid with speed v.If the electron does not hit the surface of the solenoid, maximum possible value of v is (all symbols have their standard meaning):
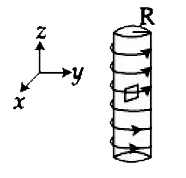 View Solution
View SolutionAn iron core solenoid of length l and cross-sectional area A having N turns on it is connected to a battery through a resistance as shown in the figure. At instant t=0, the iron rod of permeability μ from the core is abruptly removed. Find the current as a function of time.
 View Solution
View SolutionA long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.
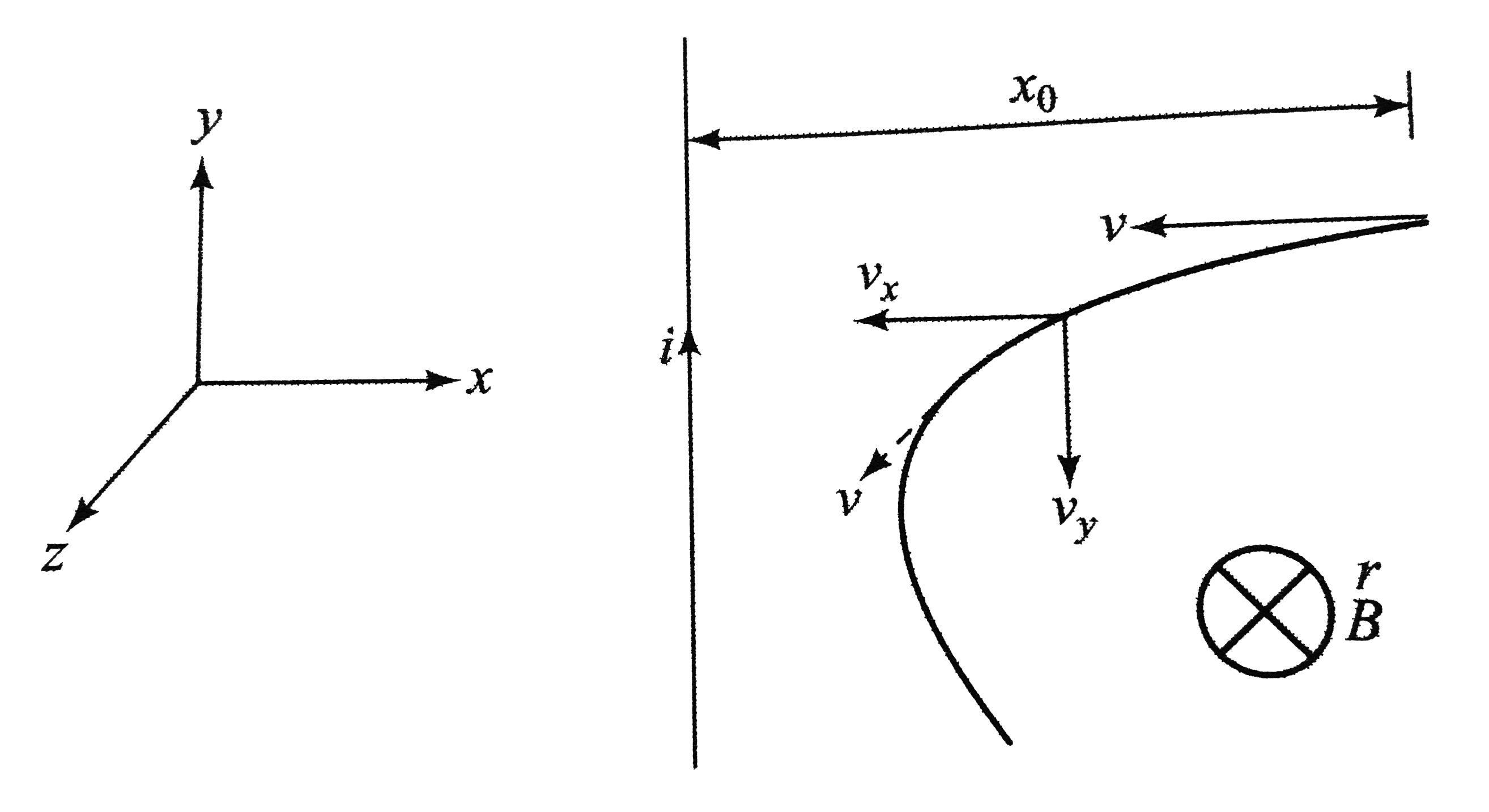
 View Solution
View SolutionA solenoid of length 'l' has N turns of wire closely spaced, each turn carrying a current i. If R is cross sectional radius of the solenoid, the magnetic induction at 'P'(only axial component).
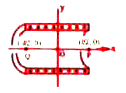 View Solution
View SolutionA long solenoid has a radius a and number of turns per unit length is n. If it carries a current i, then the magnetic field on its axis is directly proportional to
View SolutionA current l = 1.5 A is flowing through a long solenoid of diameter 3.2 cm, having 220 turns per cm. At its centre, a 130 turn closely packed coil of diameter 2.1 cm is placed such that the coil is coaxial with the long solenoid. The current in the solenoid is reduced to zero at a steady rate in 25 ms. What is the magnitude of emf induced in the coil while the current in the solenoid is changing?
View Solution

