Two particles, each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R. The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is:

Video Solution

Text Solution

Verified by Experts

Rotating charge 2q creates a current I where
$I = c h a r \frac{\geq}{t} i m e p e r i o d$ = $2 \frac{q}{2} π / ω$
$L = 2 m R^{2} ω$ , $M = I A = \frac{q \frac{ω}{π}}{π} R^{2}$
Now, $\frac{M}{L} = q r^{2} \frac{ω}{2} m R^{2} ω = \frac{q}{2} m$

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Two masses each of mass $M$ are attached to the end of a rigid massless rod of length $L$ . The moment of interia of the system about an axis passing centre of mass and perpendicular to its length is.
A $M L^{2}$ /4
B $M L^{2}$ /2
C $M L^{2}$
D $2 M L^{2}$
Question 2 - Select One
Two thin discs each of mass M and radius r metre are attached to form a rigid body as shown in figure. The rotational inertia of this body about an axis perpendicular to the plane of disc B and passing through its centre is

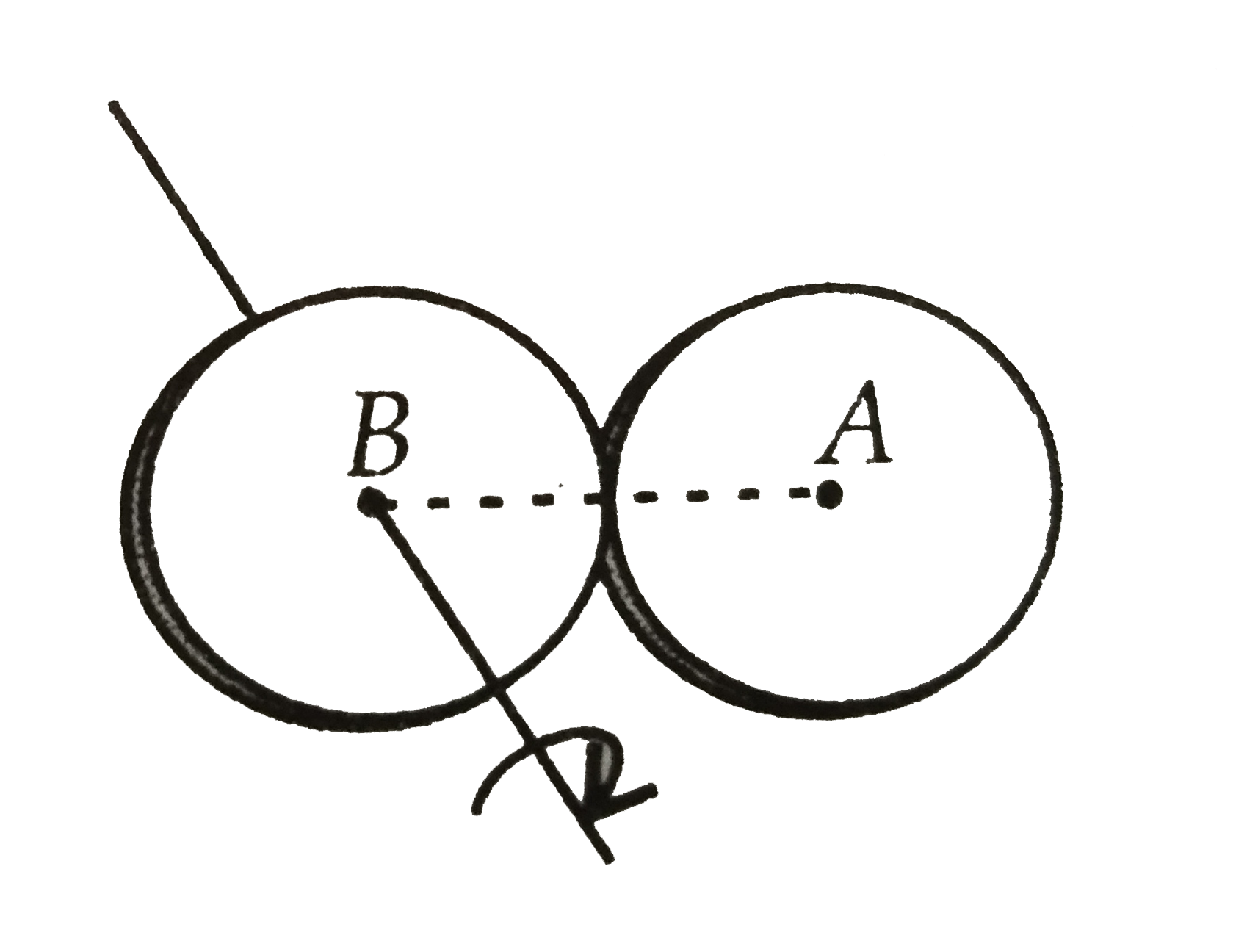A $2 M r^{2}$
B $3 M r^{2}$
C $4 M r^{2}$
D $5 M r^{2}$

VMC MODULES ENGLISH-MOVING CHARGES & MAGNETISM -Illustration

Home
Ask Doubt
Profile