If two charged particles each of charge q mass m are connected to the ends of a rigid massless rod and is rotated about an axis passing through the centre and ⊥ to length. Then find the ratio of magnetic moment to angular momentum
To find the ratio of magnetic moment to angular momentum for two charged particles connected to a rigid massless rod and rotating about an axis through the center, we can follow these steps:
Step 1: Define the System
Consider two charged particles, each with charge q and mass m, connected at the ends of a rigid massless rod of length 2r. The system rotates about an axis perpendicular to the length of the rod and passing through its center.
Step 2: Calculate the Moment of Inertia
The moment of inertia I for the two particles can be calculated as follows:
- Each particle is at a distance r from the center.
- Therefore, the moment of inertia for one particle is mr2.
- Since there are two particles, the total moment of inertia I is:
I=2⋅mr2=2mr2
Step 3: Calculate Angular Momentum
The angular momentum L of the system can be expressed as:
L=I⋅ω
Substituting the expression for I:
L=(2mr2)⋅ω
Step 4: Calculate the Current
The current I due to the rotating charges can be calculated as follows:
- The total charge Q in the system is 2q.
- The time period T for one complete revolution is given by:
T=2πω
- The current I is defined as the charge flow per unit time:
I=QT=2q2πω=2q⋅ω2π=qωπ
Step 5: Calculate Magnetic Moment
The magnetic moment μ of the system is given by:
μ=I⋅A
where A is the area of the circular path traced by the charges. The area A is:
A=πr2
Substituting the expression for current:
μ=(qωπ)⋅πr2=qωr2
Step 6: Calculate the Ratio of Magnetic Moment to Angular Momentum
Now, we can find the ratio of magnetic moment μ to angular momentum L:
μL=qωr2(2mr2)⋅ω
The ω and r2 terms cancel out:
μL=q2m
Final Answer
Thus, the ratio of magnetic moment to angular momentum is:
μL=q2m
Consider two charged particles, each with charge q and mass m, connected at the ends of a rigid massless rod of length 2r. The system rotates about an axis perpendicular to the length of the rod and passing through its center.
The moment of inertia I for the two particles can be calculated as follows:
- Each particle is at a distance r from the center.
- Therefore, the moment of inertia for one particle is mr2.
- Since there are two particles, the total moment of inertia I is:
I=2⋅mr2=2mr2
The angular momentum L of the system can be expressed as:
L=I⋅ω
Substituting the expression for I:
L=(2mr2)⋅ω
The current I due to the rotating charges can be calculated as follows:
- The total charge Q in the system is 2q.
- The time period T for one complete revolution is given by:
T=2πω
- The current I is defined as the charge flow per unit time:
I=QT=2q2πω=2q⋅ω2π=qωπ
The magnetic moment μ of the system is given by:
μ=I⋅A
where A is the area of the circular path traced by the charges. The area A is:
A=πr2
Substituting the expression for current:
μ=(qωπ)⋅πr2=qωr2
Now, we can find the ratio of magnetic moment μ to angular momentum L:
μL=qωr2(2mr2)⋅ω
The ω and r2 terms cancel out:
μL=q2m
Thus, the ratio of magnetic moment to angular momentum is:
μL=q2m
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IA
142 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB
71 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
- NUCLEAR PHYSICSBOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
3 Videos
Similar Questions
A thin uniform ring of radius R carrying charge q and mass m rotates about its axis with angular velocity ω. Find the ratio of its magnetic moment and angular momentum.
View Solution
A uniform rod of mass m is rotated about an axis passing through point O as shown. Find angular momentum of the rod about rotational law.
View Solution
Knowledge Check
Two masses each of mass M are attached to the end of a rigid massless rod of length L. The moment of interia of the system about an axis passing centre of mass and perpendicular to its length is.
AML2/4BML2/2CML2D2ML2
Consider a hypothetic spherical body. The body is cut into two parts about the diameter. One of hemispherical portion has mass distribution m while the other portion has indentical charge distribution q. The body is rotated about the axis with constant speed ω. Then, the ratio of magnetic moment to angular momentum is
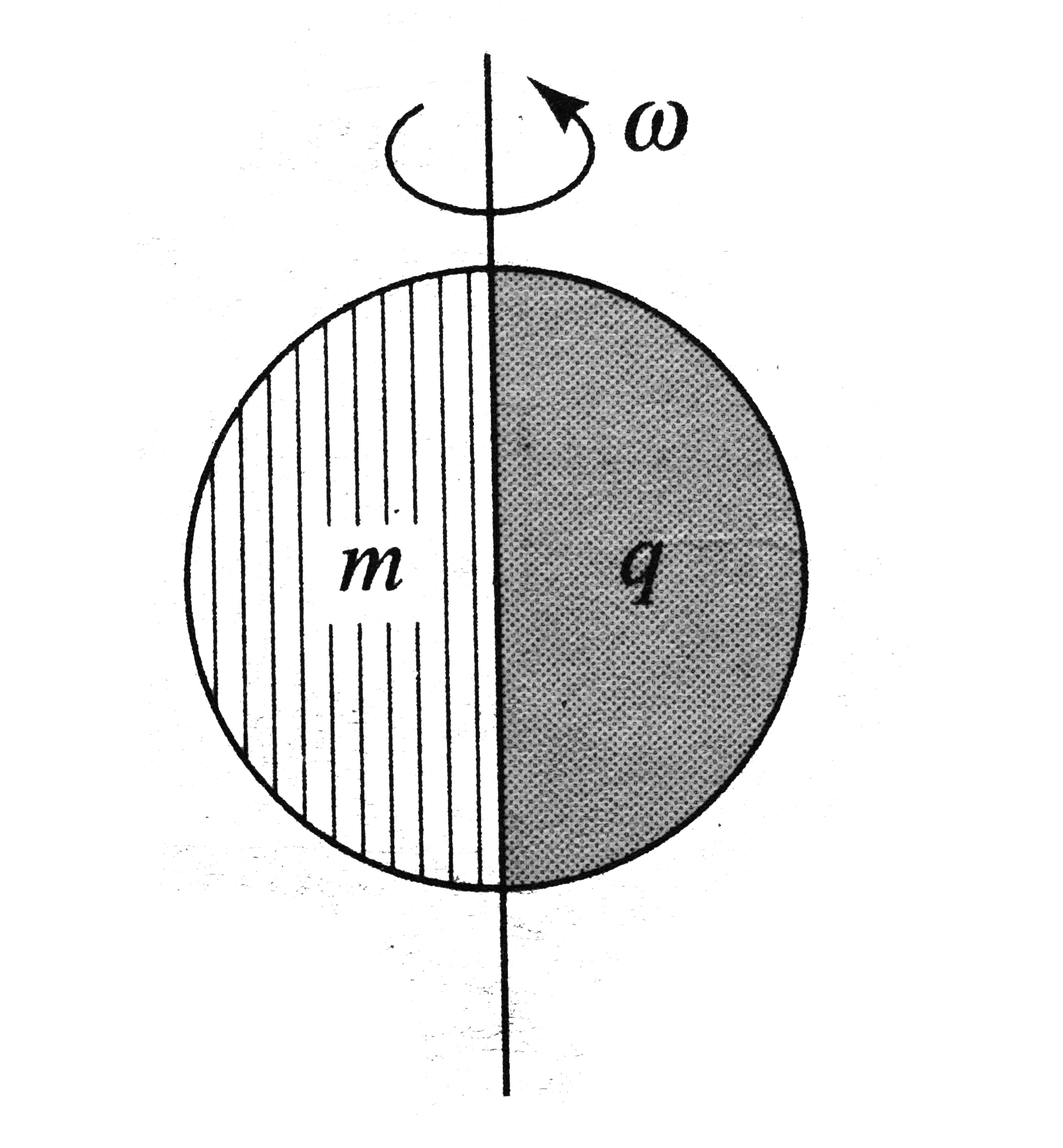
View SolutionTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
View SolutionTwo particles , each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2R . The rod is rotated at constant angular speed about a perpendicular axis passing through its centre. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the centre of the rod is
View SolutionTwo spheres each of mass M and radius R/2 are connected with a massless rod of length R. Find the moment of inertia of the system about an axis passing through the centre of one of the sphere and perpendicular to the rod
View SolutionTwo balls of masses m and 2m are attached to the ends of a light rod of length L. The rod rotates with an angular speed ω about an axis passing through the center of mass of system and perpendicular to the plane. Find the angular momentum of the system about the axis of rotation.
View SolutionA massless rod S having length 2l has equal point masses attached to its two ends as shown in figure. The rod is rotating about an axis passing through its centre and making angle α with the axis. The magnitude of change of momentum of rod i.e., ∣∣∣dLdt∣∣∣ equals
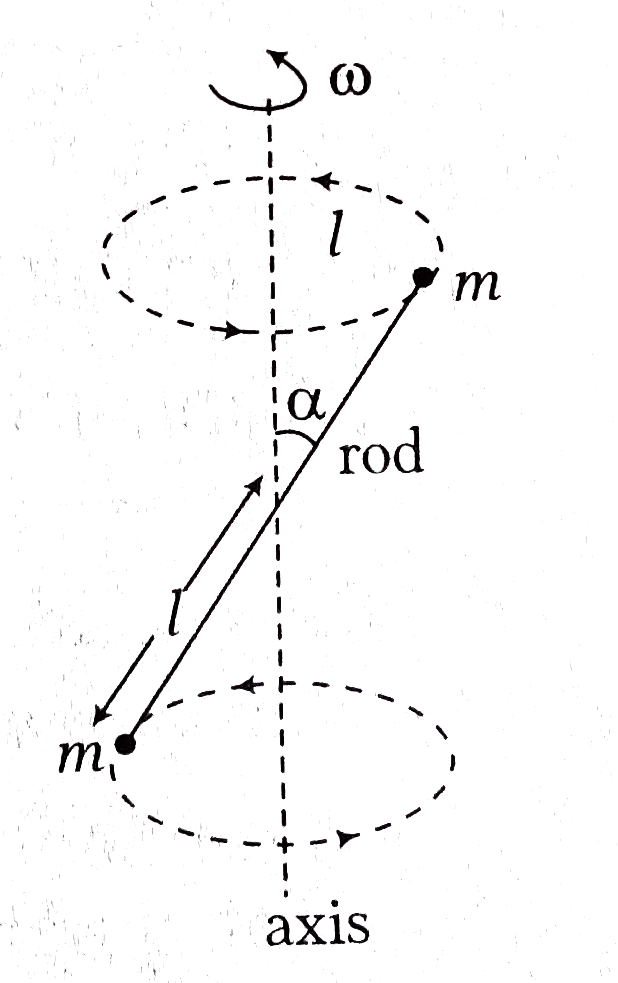
View Solutionfind moment of inertia about an axis yy which passes through the centre of mass of the two particle system as shown

View Solution
