Two coplanar circular coils of equal radius carrying currents in opposite directions are at a large distance . The distance from the first coil where the resultant magnetic induction is zero is
The correct Answer is:3
To find the distance from the first coil where the resultant magnetic induction is zero, we can follow these steps:
1. Visualize the Setup:
- We have two coplanar circular coils, Coil 1 and Coil 2, separated by a distance 'd'.
- Let the current in Coil 1 be i1 and in Coil 2 be i2. The currents are in opposite directions.
2. Define the Point of Interest:
- Let point P be at a distance x from Coil 1 and d−x from Coil 2.
3. Magnetic Field Due to a Circular Coil:
- The magnetic field B at a point on the axis of a circular coil carrying current i is given by:
B=μ0ia22(x2+a2)3/2
- Here, a is the radius of the coil.
4. Approximation:
- Since d is much greater than a, we can approximate x2+a2 as x2 when x is large compared to a.
- Thus, the magnetic field at point P due to Coil 1 becomes:
B1=μ0i1a22x3
- Similarly, for Coil 2, the magnetic field at point P is:
B2=μ0i2a22(d−x)3
5. Setting the Magnetic Fields Equal:
- For the resultant magnetic induction to be zero at point P, the magnitudes of the magnetic fields due to both coils must be equal:
B1=B2
- This leads to:
μ0i1a22x3=μ0i2a22(d−x)3
- The μ0 and a2 terms cancel out:
i1(d−x)3=i2x3
6. Rearranging the Equation:
- Expanding and rearranging gives:
i1(d−x)3=i2x3
- Taking the cube root of both sides:
(d−x)=(i2i1)1/3x
7. Solving for x:
- Rearranging gives:
d=x+(i2i1)1/3x
- Factoring out x:
d=x(1+(i2i1)1/3)
- Thus, solving for x:
x=d1+(i2i1)1/3
Final Answer:
The distance from the first coil where the resultant magnetic induction is zero is:
x=d1+(i2i1)1/3
- We have two coplanar circular coils, Coil 1 and Coil 2, separated by a distance 'd'.
- Let the current in Coil 1 be i1 and in Coil 2 be i2. The currents are in opposite directions.
- Let point P be at a distance x from Coil 1 and d−x from Coil 2.
- The magnetic field B at a point on the axis of a circular coil carrying current i is given by:
B=μ0ia22(x2+a2)3/2
- Here, a is the radius of the coil.
- Since d is much greater than a, we can approximate x2+a2 as x2 when x is large compared to a.
- Thus, the magnetic field at point P due to Coil 1 becomes:
B1=μ0i1a22x3
- Similarly, for Coil 2, the magnetic field at point P is:
B2=μ0i2a22(d−x)3
- For the resultant magnetic induction to be zero at point P, the magnitudes of the magnetic fields due to both coils must be equal:
B1=B2
- This leads to:
μ0i1a22x3=μ0i2a22(d−x)3
- The μ0 and a2 terms cancel out:
i1(d−x)3=i2x3
- Expanding and rearranging gives:
i1(d−x)3=i2x3
- Taking the cube root of both sides:
(d−x)=(i2i1)1/3x
- Rearranging gives:
d=x+(i2i1)1/3x
- Factoring out x:
d=x(1+(i2i1)1/3)
- Thus, solving for x:
x=d1+(i2i1)1/3
The distance from the first coil where the resultant magnetic induction is zero is:
x=d1+(i2i1)1/3
Topper's Solved these Questions
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - PRACTICE EXERCISE 5
5 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - PRACTICE EXERCISE 6
5 Videos
- MOVING CHARGES & MAGNETISM BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - PRACTICE EXERCISE 3
3 Videos
- Motion in Two DimensionsBOOK - VMC MODULES ENGLISHCHAPTER - Motion in Two DimensionsEXERCISE - MCQ
2 Videos
- PROPERTIES OF MATTERBOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced (Archive) Level - 2 (MATRIX MATCH TYPE)
1 Videos
Similar Questions
A circular coil of radius R carries a current i. The magnetic field at its centre is B. The distance from the centre on the axis of the coil where the magnetic field will be B/8 is
View SolutionTwo parallel wires P and Q placed at a separation
d=6cm carry electric currents i_1= 5A and i_2= 2A in <br> opposite directions as shown in figure. Find the<br> point on the line PQ where the resultant magnetic field
is zero.

View SolutionTwo parallel wires P and Q placed at a separation d =6 cm on x-axis carry electric current i1=5Aandi2=2A in opposite directions as shown in Fig. Find the point on the line PQ where the resultant mgnetic field is zero.

View SolutionTwo long straight wires, each carrying a current I in opposite directions are separated by a distance R. The magnetic induction at a point mid way between the wire is
View SolutionFor a circular coil of radius R and N turns carrying current I, the magnitude of the magnetic field at a point on its axis at a distance x from its center is given by B=μ0IR2N2(x2+R2)3/2
(a) Show that this reduces to the familiar result for field at the centre of the coil.
(b) Consider two parallel coaxial circular coils of equal radius R, and number of turns N, carrying equal currents in the same direction, and separated by a distance R. Show that the field on the axis around the mid-point between the coils is uniform over a distance that is small as compared to R and is given by B=0⋅72μ0NIR approximately.
[Such as arrangement to produce a nearly uniform magnetic field over a small region is known as Helmholtz coils.]
View SolutionA circular coil of n turns and radius r carries a current I. The magnetic field at the centre is
View SolutionTwo circular coils P & Q are coaxially & carry currents I1 and I2 respectively (all direction are w.r.t. the observer)

View SolutionTwo long parallel wires placed 0.08 m apart, carry currents 3 A and 5 A in the same direction. what is the distance from the conductor carrying the larger current to the point where the resultant magnetic field is zero?
View SolutionA circular coil of radius 2R is carrying current 'i' . The ratio of magnetic fields at the centre of the coil and at a point at a distance 6R from the centre of the coil on the axis of the coil is
View SolutionTwo long parallel wire A and B situated perpendicuilar to the plane of the paper at a distance 2a are carrying equal currents I in opposite direction as show in the figure . The value of magnetic induction at point P situated at equal distance r from both the wires will be
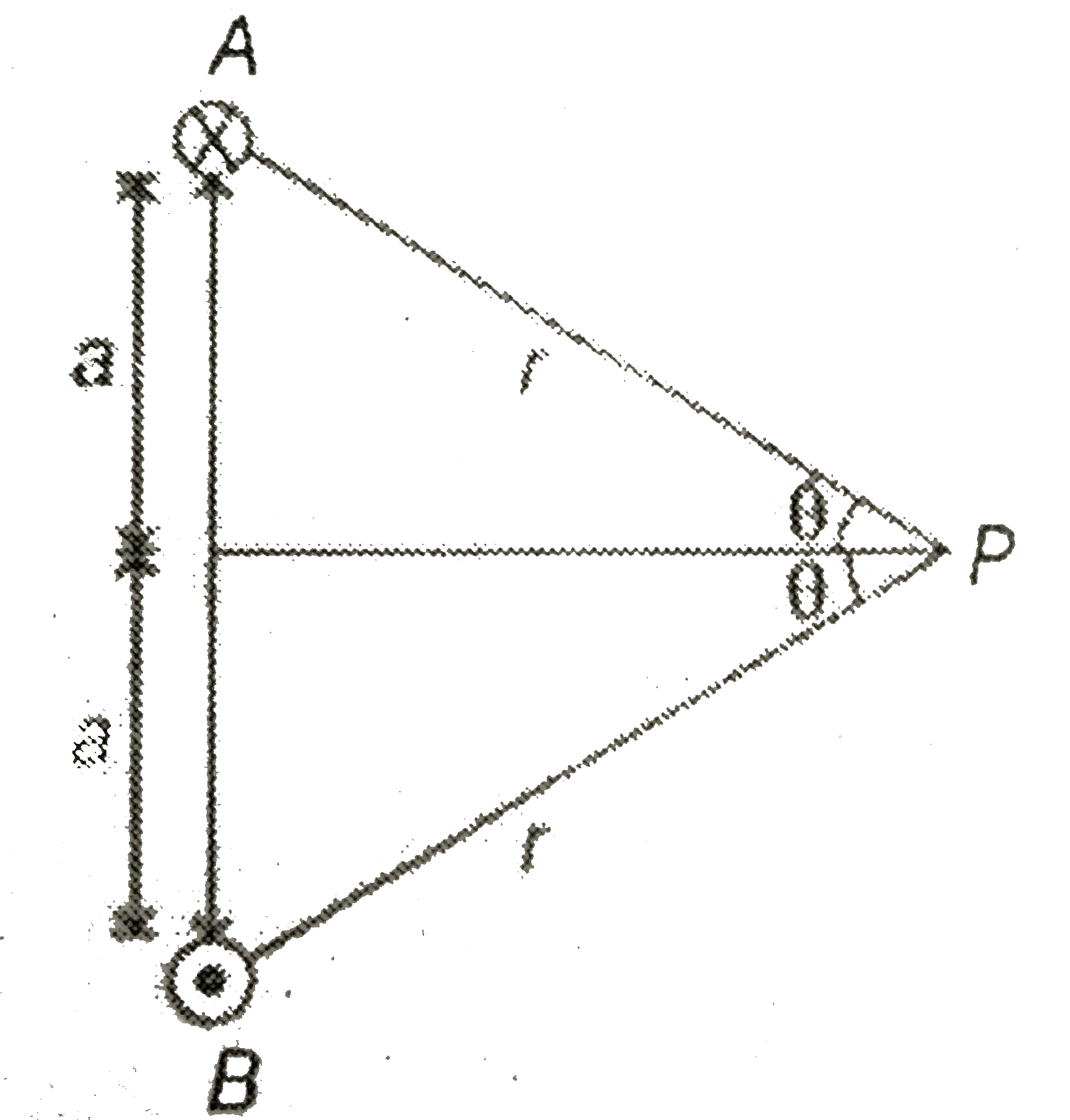
View Solution
