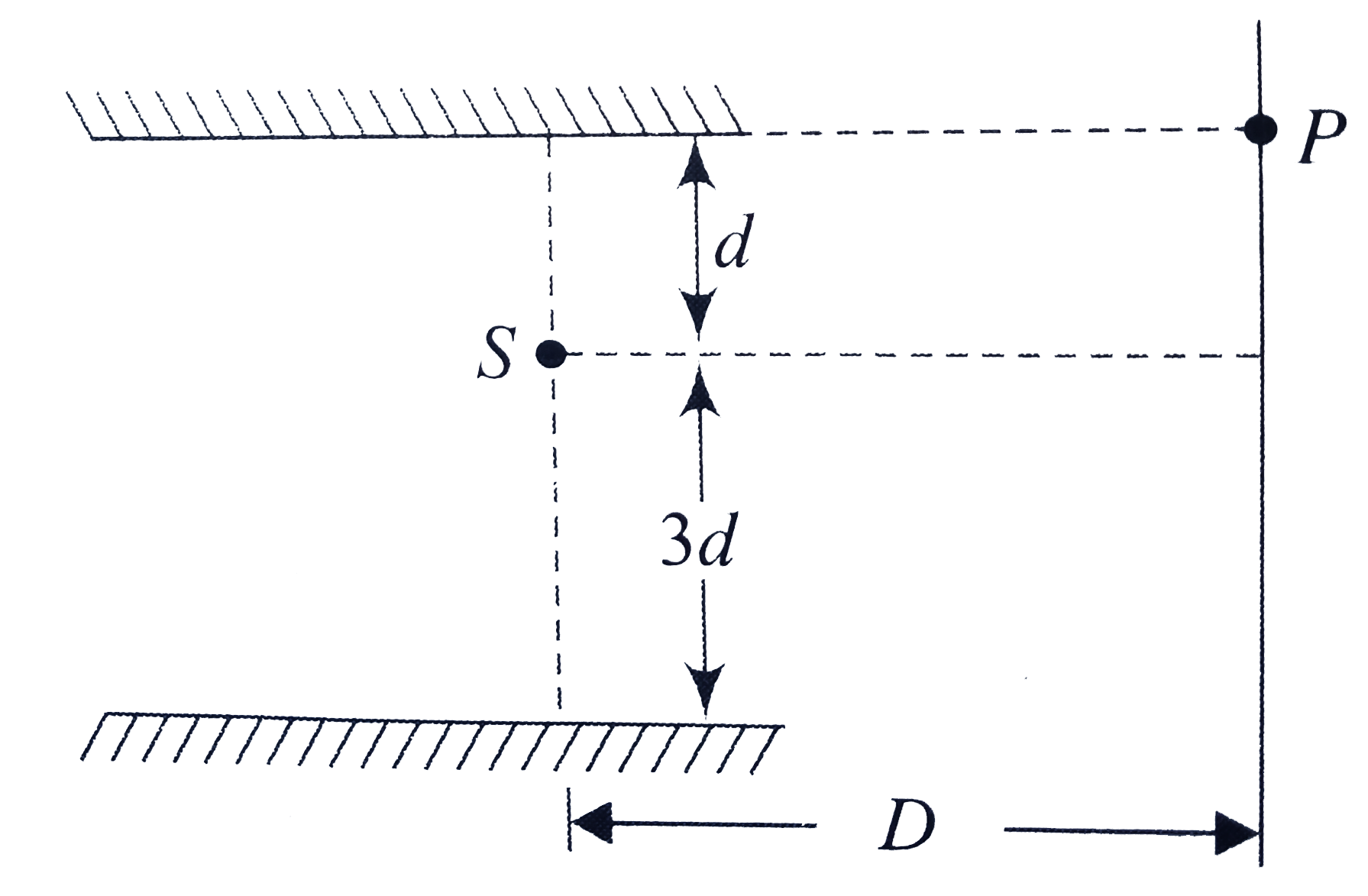
Consider the optical system shown in figure. The point source of ligth S is having wavelength equal to λ. The light is reaching screen only after reflection. For point P to be socond maxima, the value of λ would be (D>>d and d>>λ)
12d2D
6d2D
3d2D
24d2D
The correct Answer is:1
At P, Δx=(8d)×3dD. For 2nd maxima, Δx=2λ⇒24d2D=2λ⇒λ=12d2D
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - PRACTICE EXERCISE-11videos
RAY OPTICS
- BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - PRACTICE EXERCISE-21videos
RAY OPTICS
- BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - IN-CHAPTER EXERCISE-J10videos
RAY OPTICS
- BOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS30videos
QUIZ
- BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS AND WAVE OPTICS EXERCISE - IMPECCABLE58videos
RAY OPTICS AND WAVE OPTICS
Similar Questions
Four monochromatic and coherent sources of light, emitting waves in phase of wavelength λ, are placed at the points x = 0, d 2d and 3d on the x-axis. Then
View SolutionLight of wavelength λ is incident on a slit of width d and distance between screen and slit is D. Then width of maxima and width of slit will be equal if D is
View Solution
Knowledge Check
- Question 1 - Select One
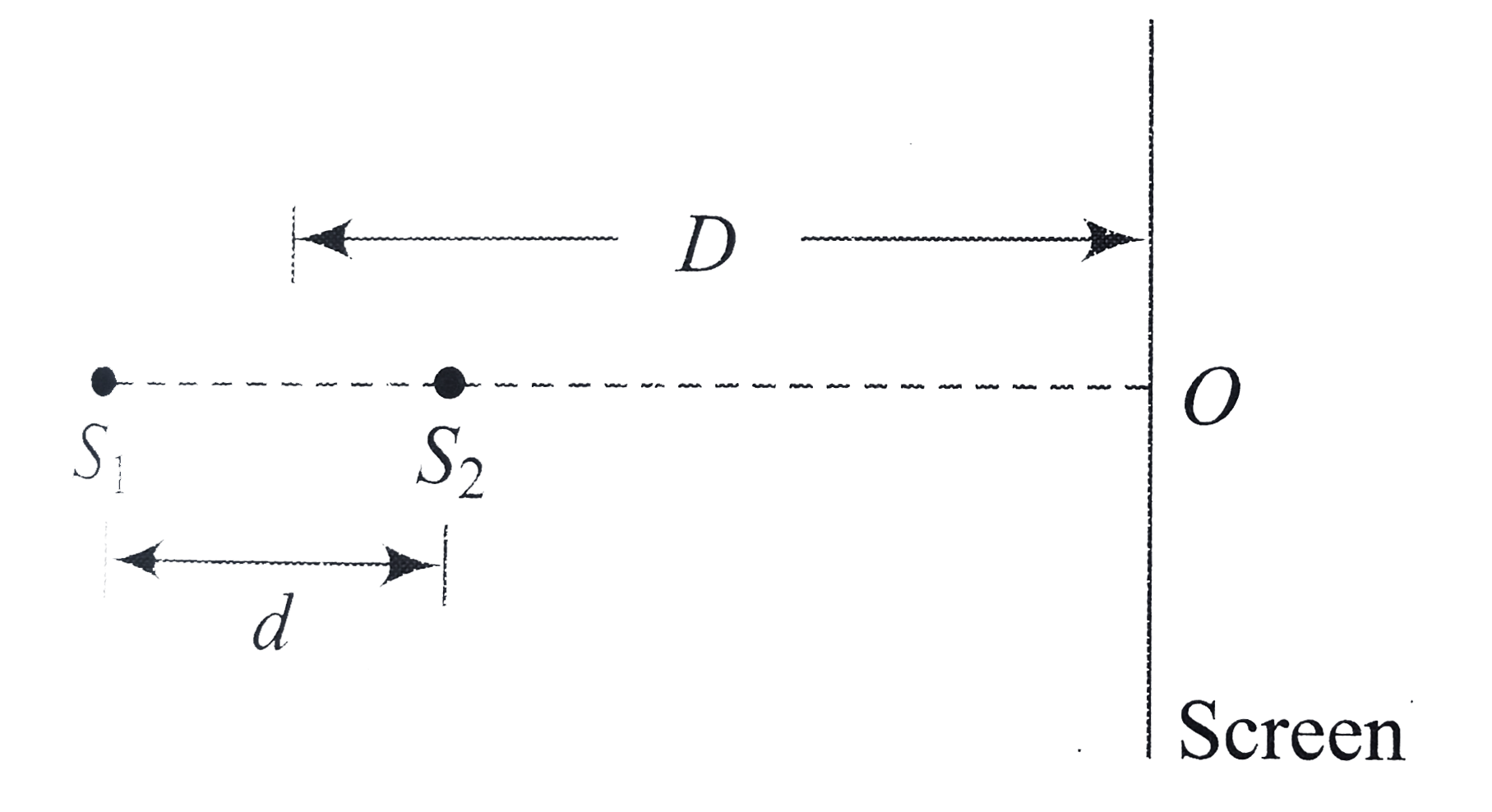
Two points nonochromatic and coherent sources of light of wavelength λ each are placed as shown in figure. The initial phase difference between the sources is zero O. (d>>d). Mark the correct statement(s).
 AIf d=7λ2,O will be minima.BIf d=λ, only one maxima can be observed on screen.CIf d=4.8λ then total 10 minimas would be there on screen.DIf d=5λ2, then intensity at O would be maximum.
AIf d=7λ2,O will be minima.BIf d=λ, only one maxima can be observed on screen.CIf d=4.8λ then total 10 minimas would be there on screen.DIf d=5λ2, then intensity at O would be maximum.
Consider a two slit interference arrangements such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
 View Solution
View SolutionFollowing figures shows sources S1 and S2 that emits light of wavelength λ in all directions. The sources are exactly in phase and are separated by a distance equal to 1.5λ. If we start at the indicated start point and travel along path 1 and 2, the interference produce a maxima all along
 View Solution
View SolutionA driver is riding a car with velocity vc between two vertical walls on a horizontal surface as shown in figure.A source of sound of frequency 'f' is situated on the car. (vc<<v, where v is the speed of sound in air )

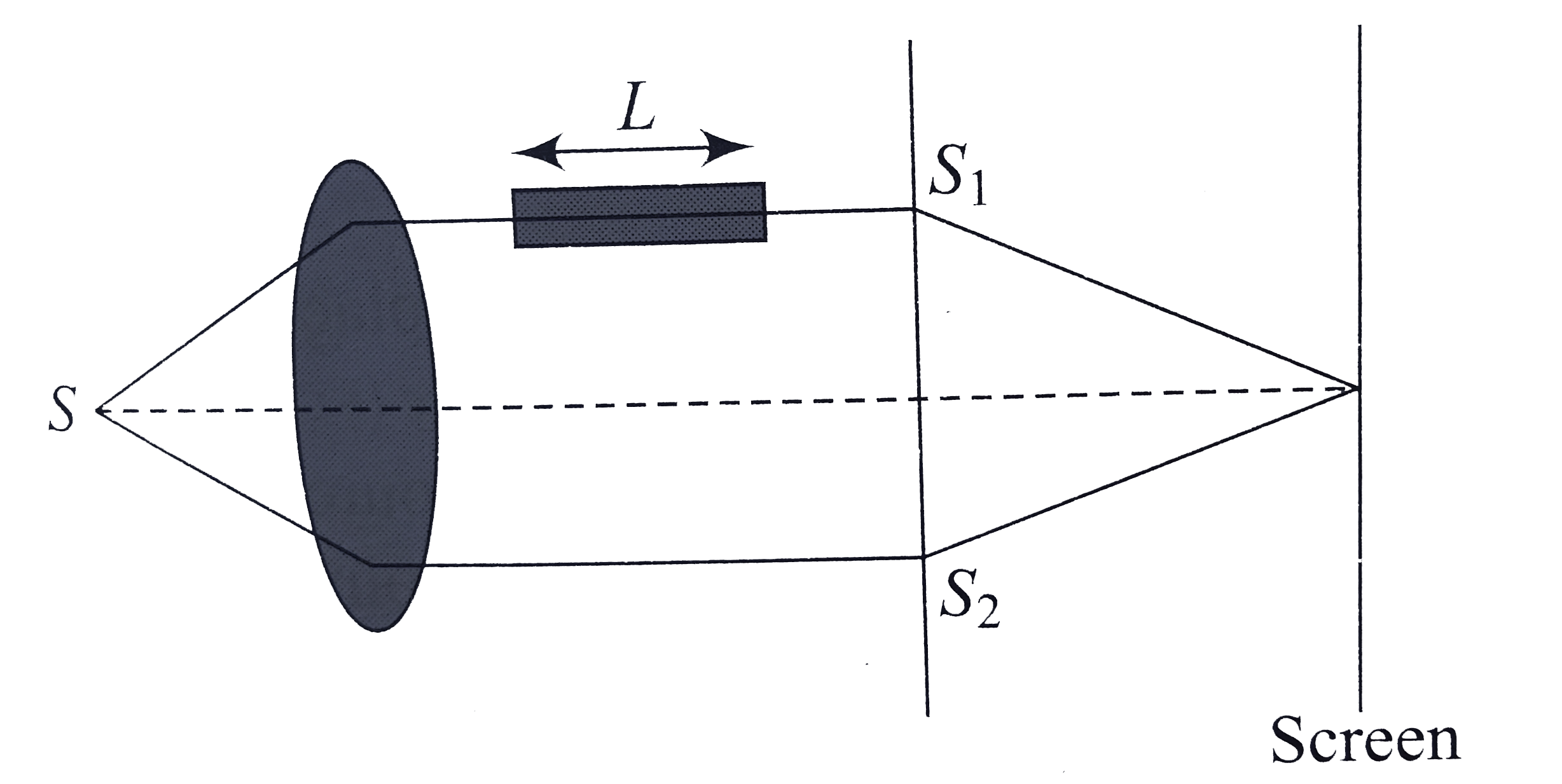
Consider the sound wave observed by the driver directly from car has a wavelength λ1 and the sound wave after reflection from wall-1 observed by the driver has wavelength λ2 then λ1−λ2λ1+λ2 is :View SolutionFigure shows a narrow slit S illuminated b a monochromatic light of wavelength λ in a double-slit experiment. In the path of the rays reaching the upper slit S1, a tube to length L is interposed in which the index of reflection of the medium varies linearly as shown in figure . The position of the central maximum in the interference pattern on the screen was displaceed by N fringes. Find the value of N in terms of μ0, L and λ.
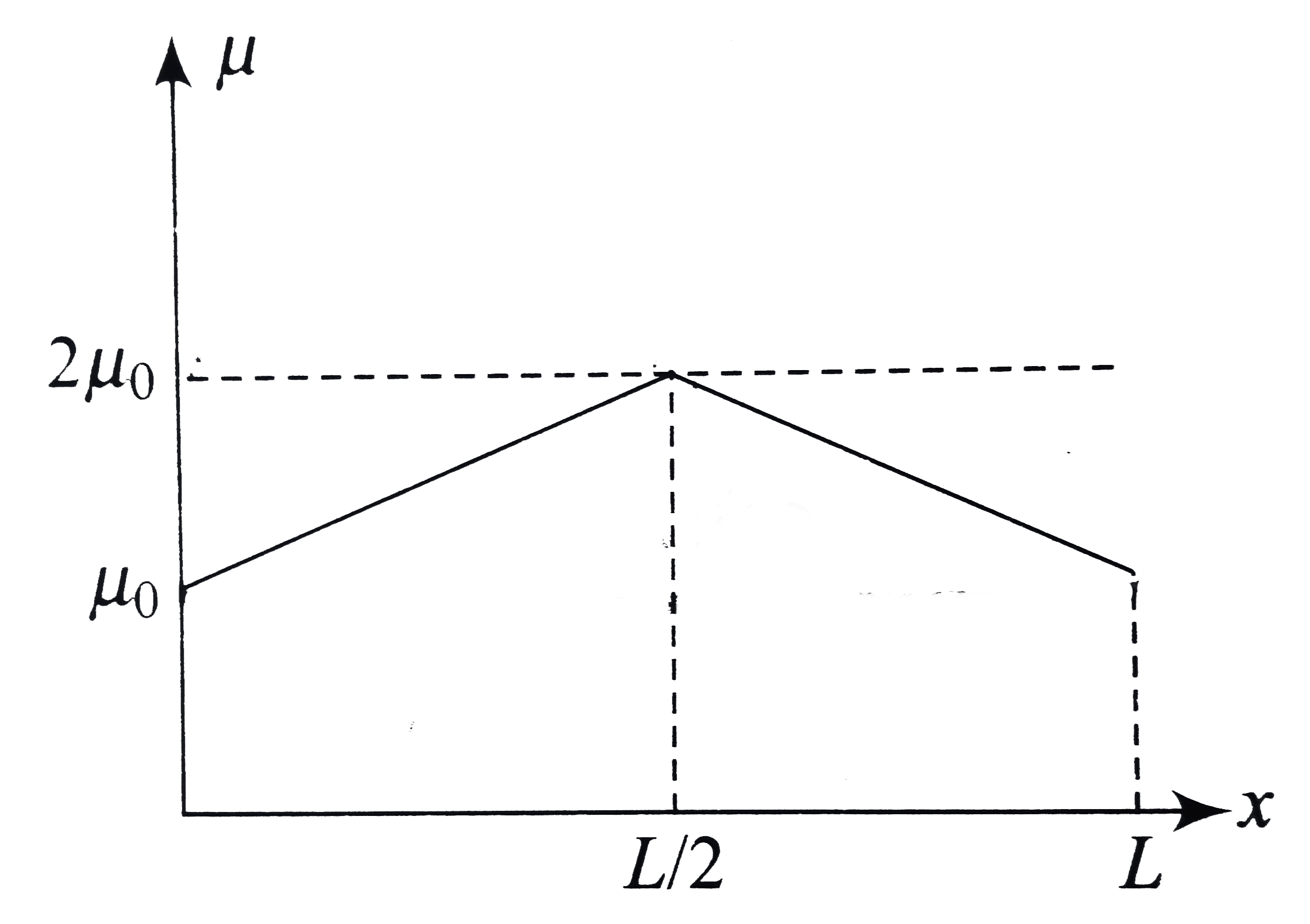 View Solution
View SolutionA sound source emits two sinusoidal sound waves, both of wavelength λ, along paths A and B as shown in figure.The sound travelling along path B is reflected from five surfaces as shown and then merges at point Q, producing minimum intensity at that point.The minimum value of d in terms of λ is :
 View Solution
View SolutionTwo coherent sources S1 and S2 are kept on the edges of a step as shown in the figure. An infinitely long screen is placed on the right side of sources and lies at along y−z plane. Calculate total no. of maximas observed on the screen. PS1=8λ and PS2=6λ. Where λ is wavelength of light used. (There is no reflection from steps)
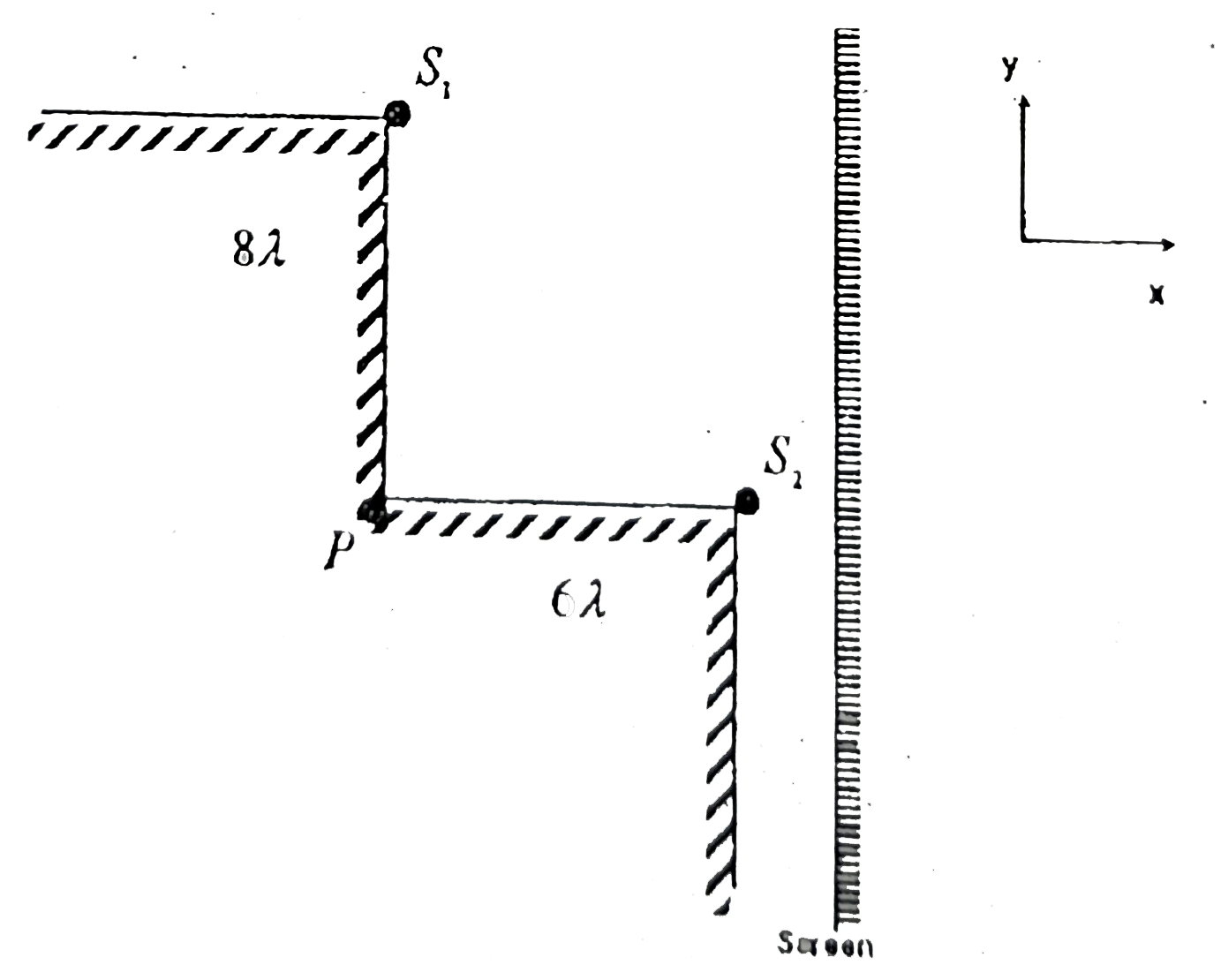 View Solution
View SolutionIn the figure shown S is the saurce of white light kept at a distance x0 frorn the plane of the slits. The source moves with a constant specd u towards the slits on the line perpendicular to the plane of the slits and passing through the slit S1. Find the instanteneous velocity (magnituce and direction). of the central maxima at time t having range 0≤t<<x0−du. Assume that D>>d.
 View Solution
View Solution

