With respect to air critical angle in a medium for light of red colour [λ1] is θ. Other facts remaining same, critical angle for light of yellow colour [λ2] will be
θ
More than θ
Less than θ
θλ1λ2
The correct Answer is:3
To solve the problem regarding the critical angle for light of different colors (red and yellow), we can follow these steps:
1. Understanding Critical Angle:
The critical angle (Ic) is defined as the angle of incidence above which total internal reflection occurs. It is related to the refractive index (μ) of the medium by the formula:
sin(Ic)=1μ
2. Given Information:
- The critical angle for red light (wavelength λ1) is given as θ.
- We need to find the critical angle for yellow light (wavelength λ2).
3. Wavelength Comparison:
It is known that red light has a longer wavelength than yellow light:
λ1>λ2
4. Refractive Index Relation:
The refractive index (μ) of a medium is inversely proportional to the wavelength of light:
μ∝1λ
Therefore, since λ1 > λ2, we can conclude:
μ1<μ2
where μ1 is the refractive index for red light and μ2 is the refractive index for yellow light.
5. Critical Angle for Yellow Light:
Since μ2 > μ1, we can analyze the critical angles:
sin(IC1)=1μ1(for red light)
sin(IC2)=1μ2(for yellow light)
Because μ2 > μ1, it follows that:
1μ2<1μ1
Thus:
sin(IC2)<sin(IC1)
6. Conclusion:
Since the sine of the critical angle for yellow light is less than that for red light, we can conclude that:
IC2<IC1
Therefore, the critical angle for yellow light (I_{C2}) is less than θ (the critical angle for red light).
Final Answer:
The critical angle for yellow light will be less than θ.
The critical angle (Ic) is defined as the angle of incidence above which total internal reflection occurs. It is related to the refractive index (μ) of the medium by the formula:
sin(Ic)=1μ
- The critical angle for red light (wavelength λ1) is given as θ.
- We need to find the critical angle for yellow light (wavelength λ2).
It is known that red light has a longer wavelength than yellow light:
λ1>λ2
The refractive index (μ) of a medium is inversely proportional to the wavelength of light:
μ∝1λ
Therefore, since λ1 > λ2, we can conclude:
μ1<μ2
where μ1 is the refractive index for red light and μ2 is the refractive index for yellow light.
Since μ2 > μ1, we can analyze the critical angles:
sin(IC1)=1μ1(for red light)
sin(IC2)=1μ2(for yellow light)
Because μ2 > μ1, it follows that:
1μ2<1μ1
Thus:
sin(IC2)<sin(IC1)
Since the sine of the critical angle for yellow light is less than that for red light, we can conclude that:
IC2<IC1
Therefore, the critical angle for yellow light (I_{C2}) is less than θ (the critical angle for red light).
The critical angle for yellow light will be less than θ.
Topper's Solved these Questions
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - IN-CHAPTER EXERCISE-C
10 Videos
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - IN-CHAPTER EXERCISE-D
9 Videos
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - IN-CHAPTER EXERCISE-A
10 Videos
- QUIZBOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS
30 Videos
- RAY OPTICS AND WAVE OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS AND WAVE OPTICS EXERCISE - IMPECCABLE
58 Videos
Similar Questions
Knowledge Check
Critical angle for light going from medium (i) to (ii) is θ . The speed of light in medium (i) is v then speed in medium (ii) is
Av(1−cosθ)BvsinθCvcosθDv(1−sinθ)
The critical angle of light from medium A to medium B is θ. The speed of light in medium A is v. the speed of light in medium B is
View SolutionCritical angle of light passing from glass to air is least for
View SolutionWhich colour of light travels fastest in any medium except air ?
View SolutionThe critical angle for light going from medium X into medium Y is θ . The speed of light in medium X is v. The speed of light in medium Y is
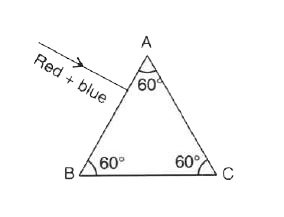
View SolutionThe diagram alongside shows a beam of light (red + blue) incident normally on an equilateral triangular prism. If the critical angle for the material of prüsm is 60∘ for the light of red colour, complete the diagram showing the path of light of each colour emerging out of the prism. Mark in the diagram the angles wherever necessary.
View SolutionFind the angle of refraction in a medium (μ=2) if light is incident in vacuum, making an angle equal to twice the critical angle.
View SolutionCalculate the speed of light in a medium whose critical angle is 30∘.
View Solution
