Light wave enters from medium 1 to medium 2. Its velocity in 2nd medium is double from 1st. For total internal reflection the angle of incidence must be greater than
30∘
60∘
45∘
90∘
The correct Answer is:1
To solve the problem, we need to determine the critical angle for total internal reflection when light transitions from medium 1 to medium 2, where the velocity of light in medium 2 is double that in medium 1.
1. Understanding the Problem:
- We have two media: medium 1 (with velocity V1) and medium 2 (with velocity V2).
- It is given that V2=2V1.
2. Using the Relationship of Refractive Index:
- The refractive index μ of a medium is defined as:
μ=cV
where c is the speed of light in vacuum and V is the speed of light in the medium.
- Therefore, for medium 1:
μ1=cV1
- For medium 2:
μ2=cV2=c2V1=12⋅cV1=μ12
3. Applying Snell's Law:
- According to Snell's law:
μ1sinic=μ2sinr
- For total internal reflection, the angle of refraction r is 90∘. Thus, sinr=1.
- Therefore, we can write:
μ1sinic=μ2
4. Substituting the Values:
- Substitute μ2=μ12 into the equation:
μ1sinic=μ12
- Dividing both sides by μ1 (assuming μ1≠0):
sinic=12
5. Finding the Critical Angle:
- The angle whose sine is 12 is 30∘:
ic=30∘
6. Conclusion:
- For total internal reflection to occur, the angle of incidence i must be greater than the critical angle ic:
i>30∘
Final Answer:
The angle of incidence must be greater than 30∘.
---
- We have two media: medium 1 (with velocity V1) and medium 2 (with velocity V2).
- It is given that V2=2V1.
- The refractive index μ of a medium is defined as:
μ=cV
where c is the speed of light in vacuum and V is the speed of light in the medium.
- Therefore, for medium 1:
μ1=cV1
- For medium 2:
μ2=cV2=c2V1=12⋅cV1=μ12
- According to Snell's law:
μ1sinic=μ2sinr
- For total internal reflection, the angle of refraction r is 90∘. Thus, sinr=1.
- Therefore, we can write:
μ1sinic=μ2
- Substitute μ2=μ12 into the equation:
μ1sinic=μ12
- Dividing both sides by μ1 (assuming μ1≠0):
sinic=12
- The angle whose sine is 12 is 30∘:
ic=30∘
- For total internal reflection to occur, the angle of incidence i must be greater than the critical angle ic:
i>30∘
The angle of incidence must be greater than 30∘.
Topper's Solved these Questions
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - IN-CHAPTER EXERCISE-C
10 Videos
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - IN-CHAPTER EXERCISE-D
9 Videos
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - IN-CHAPTER EXERCISE-A
10 Videos
- QUIZBOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS
30 Videos
- RAY OPTICS AND WAVE OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS AND WAVE OPTICS EXERCISE - IMPECCABLE
58 Videos
Similar Questions
Under what conditions is the phenomenon of total internal reflection between the critical angle of incidence and the refractive index of the medium.
View SolutionIn total internal reflection when the angle of incidence is equal to the critical angle for the pair of medium in contact, what will be angle of refraction? In total internal reflection when the angle of incidence is equal to the critical angle for the pair of medium in contact, what will be angle of refraction? In total internal reflection when the angle of incidence is equal to the critical angle for the pair of medium in contact, what will be angle of refraction?
View Solution
Knowledge Check
When a light ray enters from a denser medium to a rarer medium.
AThe light ray bends towards the normal.BAngle of incidence is less than angle of refraction.CSpeed of light decreases.DSpeed of light remains unchanged.
A ray of light is incident from a denser to a rarer medium. The critical angle for total internal reflection is θic and Brewster's angle of incidence is θiB such that sinθicsinθiB=η=1.28 . The relative refractive index of the two media is
View SolutionA light beam passes from medium 1 to medium 2. Show that the emerging beam is parallel to the incident beam.
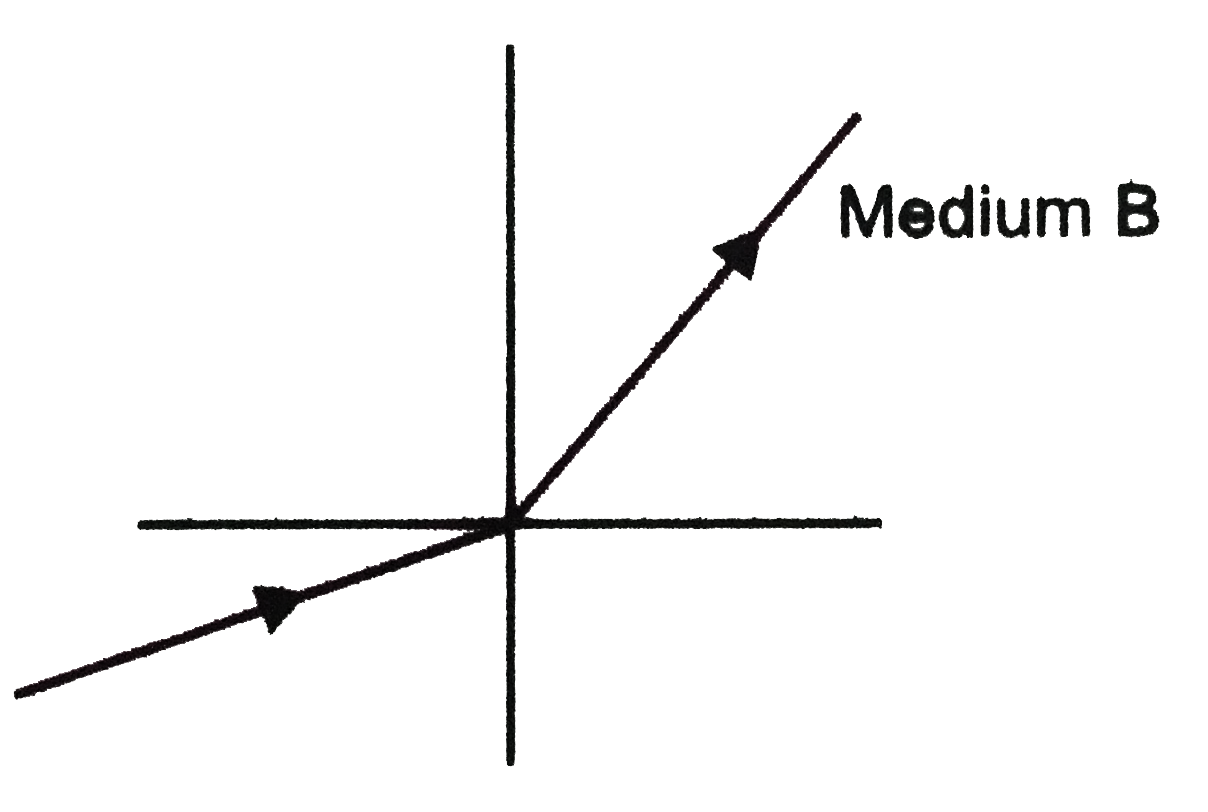
View SolutionA light ray enters from medium A to medium B as shown in Figure. The refractive index of medium A relative to B will be
View SolutionA ray of light passes from vaccum into a medium of refractive index n. If the angle of incidence is twice the angle of refraction, then the angle of incidence is
View SolutionA sound waves passes from a medium A to a medium B. The velocity of sound in B is greater than in A. Assume that there is no absorption or reflection at the boundary . As the wave moves across the boundary :
View SolutionA light beam, passes from medium 1 to medium 2. Show that the emerging beam is parallel to the incident beam.
View SolutionIf critical angle for TIR from medium to vacuum is 45 deg then velocity of light in medium
View Solution
